第四周算法题(单调队列，单调栈，全排列，trie树)

第四周(11.13-11.19)

第一题：P1886 滑动窗口 /【模板】单调队列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目来源

题目描述

给定一个大小为 n≤10e6 的数组。

有一个大小为 k的滑动窗口，它从数组的最左边移动到最右边。

你只能在窗口中看到 k个数字。

每次滑动窗口向右移动一个位置。

以下是一个例子：

该数组为 [1 3 -1 -3 5 3 6 7]，k 为 3。

窗口位置	最小值	最大值
[1 3 -1] -3 5 3 6 7	-1	3
1 [3 -1 -3] 5 3 6 7	-3	3
1 3 [-1 -3 5] 3 6 7	-3	5
1 3 -1 [-3 5 3] 6 7	-3	5
1 3 -1 -3 [5 3 6] 7	3	6
1 3 -1 -3 5 [3 6 7]	3	7

你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式

输入包含两行。

第一行包含两个整数 n和 k，分别代表数组长度和滑动窗口的长度。

第二行有 n个整数，代表数组的具体数值。

同行数据之间用空格隔开。

输出格式

输出包含两个。

第一行输出，从左至右，每个位置滑动窗口中的最小值。

第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例：

8 3
1 3 -1 -3 5 3 6 7

输出样例：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

解题思路:

1. 这段代码的目标是在一个数组中找到每个长度为 k 的子数组的最小值和最大值。这是通过使用一个双端队列 que 来实现的，队列中存储的是数组元素的值，而不是索引。

   下面是这段代码的详细解释：

   1. 初始化变量：n 和 k 分别表示数组的长度和子数组的长度。arr 是输入的数组，que 是用来存储子数组元素的队列。l 和 r 分别表示队列的头部和尾部。
   2. 输入数组：通过 scanf 函数读取 n 和 k 的值，然后读取 n 个整数填充数组 arr。
   3. 寻找最小值：
      • 遍历数组 arr，对于每个元素 arr[i]，如果队列不为空且 arr[i] 小于队列尾部的元素，那么就将队列尾部的元素出队，直到队列为空或者 arr[i] 不小于队列尾部的元素。然后将 arr[i] 入队。
      • 如果当前元素的索引 i 大于等于 k，并且队列头部的元素等于窗口的第一个元素（即 arr[i-k]），那么就将队列头部的元素出队。
      • 如果当前元素的索引 i 大于等于 k-1，那么就输出队列头部的元素，因为它就是当前窗口的最小值。
   4. 寻找最大值：这部分的代码与寻找最小值的代码非常相似，只是在比较元素大小时的条件相反。如果 arr[i] 大于队列尾部的元素，那么就将队列尾部的元素出队，然后将 arr[i] 入队。

解题代码:

#include 
int que[1000005];
int arr[1000005] = { 0 };
int l = 0, r = 0;
int main() {
    int n, k;
    scanf("%d %d", &n, &k);
    for (int i = 0; i < n; i++) scanf("%d", &arr[i]);
    //MIN
    for (int i = 0; i < n; i++) {
        while (l < r && arr[i] < que[r - 1]) {
            r--;
        }
        que[r++] = arr[i];
        if (i >= k && que[l] == arr[i - k]) {
            l++;
        }
        if (i >= k - 1) {
            printf("%d ", que[l]);
        }
    }
    printf("\n");
    l = 0, r = 0;
    //MAX
    for (int i = 0; i < n; i++) {
        while (l < r && arr[i] > que[r - 1]) {
            r--;
        }
        que[r++] = arr[i];
        if (i >= k && que[l] == arr[i - k]) {
            l++;
        }
        if (i >= k - 1) {
            printf("%d ", que[l]);
        }
    }
    return 0;
}

问题与反思：

1.这道题的关键在于如何维护队列和在什么时候开始输出元素，首先要注意的是r，r并非是尾值，r-1才是尾值，而l却是头值，因此当l==r时，就当作为队列为空。

2.接上，顺序也很重要，要先储存，再删除，毕竟很有可能当前读入的值或者删除的值就是最大最小值，先输出会出错。

3.第三，关于输出，最开始我用r-l>=k来判断，一直出错，原因在于，我们的队列只是模拟一种储存方式，而不是模拟窗口本身，有可能里面只有一个元素，所有用i>k-1。

4.代码最难的一步是队头的处理，基于3，里面并不是模拟的窗口，那我们如何得知什么时候能删除队头？

(i >= k && que[l] == arr[i - k]) 很关键，i>=k说明可以开始删元素，而que[l] == arr[i - k]说明已经滑动到了应该删除的位置。

第二题：

题目来源：P5788 【模板】单调栈 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目描述

给出项数为 n 的整数数列 。

找出这项数列每一项后面的数中第一个比他大的数的下标，没有就输出0。

输入格式

第一行一个正整数n。

第二行 n 个正整数ai。

输出格式

一行 n 个整数表示下标的值。

输入样例

5
1 4 2 3 5

输出

2 5 4 5 0

说明/提示

【数据规模与约定】

对于 30%的数据，n≤100；

对于 60%的数据，1≤n<=5×10e3

对于 100%的数据，1≤n≤3×10e6，1≤ai≤10e9。

解题代码：

#include  // 引入标准输入输出库

int main() // 主函数
{
	int n; // 定义整数 n，用于存储数组的大小
	int l = 0,r = 0; // 定义两个整数 l 和 r，初始化为 0，用于作为栈的左右指针
	scanf("%d", &n); // 从标准输入读取 n 的值

	int arr[3000001]; // 定义一个大小为 3000001 的整数数组 arr
	int i; // 定义整数 i，用于循环
	for ( i = 0; i < n; i++) // 对于每一个 i，从 0 到 n-1
	{
		scanf("%d", &arr[i]); // 从标准输入读取 arr[i] 的值
	}

	int ans[3000001] = { 0 }; // 定义一个大小为 3000001 的整数数组 ans，并初始化所有元素为 0
	int stack[3000001] = { 0 }; // 定义一个大小为 3000001 的整数数组 stack，并初始化所有元素为 0

	for ( i = 0; i < n; i++) { // 对于每一个 i，从 0 到 n-1
		while (r > l && arr[i] > arr[stack[r-1]]) { // 当 r 大于 l 且 arr[i] 大于栈顶元素时
			ans[stack[r-1]] = i + 1; // 将 ans 数组的对应位置更新为 i + 1
			r--; // r 减 1，即出栈
		}
		stack[r++] = i; // 将 i 压入栈中，然后 r 加 1
	}

	for ( i = 0; i < n; i++) // 对于每一个 i，从 0 到 n-1
		printf("%d ", ans[i]); // 打印 ans[i] 的值和一个空格

    printf("\n"); // 打印一个换行符
    return 0; // 主函数返回 0，表示程序正常结束
}

解题思路：

这段代码的主要目的是找出数组中每个元素右边第一个比它大的元素的位置。它使用了一个栈来存储尚未找到右边更大元素的元素的索引。当找到一个更大的元素时，它会更新答案数组并将栈顶元素出栈，直到栈为空或者栈顶元素大于当前元素。然后，它会将当前元素的索引压入栈中。最后，它打印出答案数组的所有元素。主要关键在于压入和弹出，如果比栈小（或者等于），直接让他作为栈顶，不然的话，就弹出栈顶元素，一直循环到比他小为止，并且记录是谁（下标）弹出了它，即是第一个比他大的数，可以简单的记忆：

比他小的压不动，就堆在上面，比他大的一直压，压到它为止，即第一个最大。

第三题：

题目来源：https://www.acwing.com/problem/content/description/844/

题目描述：

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法，现在，请你按照字典序将所有的排列方法输出。

输入格式

共一行，包含一个整数 n。

输出格式

按字典序输出所有排列方案，每个方案占一行。

数据范围

1≤n≤7

输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

解题思路：

这是一道经典的全排列的问题，在接下来的代码中，将会用到DFS算法，DFS做不来，或者根本想不到这一点，看题解都看了半天(太废了。。。)先笔记一下DFS:

深度优先搜索算法（Depth First Search，简称DFS）：一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件，搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度)为O(!n)。

解题代码:

#include 
int path[10000]={0};
int n;
int state[10000]={0};
void print(int x){
	if(x==n){
		for(int i=0;i<n;i++){
			printf("%d ",path[i]);
		}
		printf("\n");
	}
	else{
	  for(int j=1;j<=n;j++){
	  	if(state[j]==0){
	  		path[x]=j;
	  		state[j]=1;
	  		print(x+1);
	  		state[j]=0;
		  } 	  	
	  }			
	}	
}
int main(){
	scanf("%d",&n);
	print(0);	
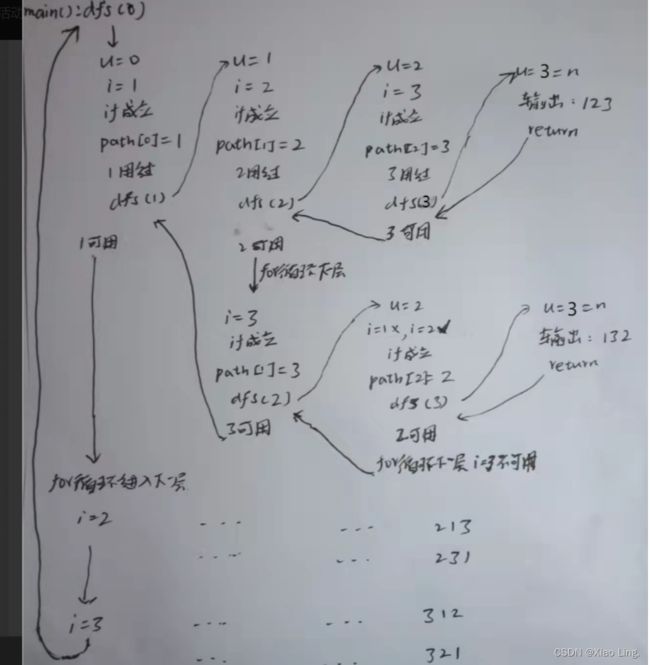
	return 0;
} 

先上图：

（图片来自一位大佬…)

DFS的关键在于两种思想，递归和回溯思想，需要注意的是，每一次遍历都从1开始的，递归结束后，并不是就一直state[i]=0，然后结束，需要注意的是，这是一个循环，而不是顺序结构，只有当j==n时，循环才是真的结束。

第四题：

题目来源：https://www.acwing.com/problem/content/837/

题目描述:

维护一个字符串集合，支持两种操作：

1. I x 向集合中插入一个字符串 x；
2. Q x 询问一个字符串在集合中出现了多少次。

共有 N 个操作，所有输入的字符串总长度不超过 105，字符串仅包含小写英文字母。

输入格式

第一行包含整数 N，表示操作数。

接下来 N 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式

对于每个询问指令 Q x，都要输出一个整数作为结果，表示 x在集合中出现的次数。

每个结果占一行。

数据范围

1≤N≤2∗10^4

输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
0
1

解题代码：

#include 
#include 
#define N 100010
int son[N][26], cnt[N], idx;
char str[N];
void insert(char* str)
{
    int p = 0; 
    for (int i = 0; str[i]; i++)
    {
        int u = str[i] - 'a'; 
        if (!son[p][u]) son[p][u] = ++idx;   
        p = son[p][u];  
    }
    cnt[p]++; 
}
int query(char* str)
{
    int p = 0;
    for (int i = 0; str[i]; i++)
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0; 
        p = son[p][u];
    }
    return cnt[p];  
}
int main()
{
    int m;
    scanf("%d",&m);
while (m--)

  {
      char op[2];
      scanf("%s%s", op, str);

  if (*op == 'I') insert(str);
  else printf("%d\n", query(str));

  }
return 0;
}

解题思路：

本题用了trie树的算法，对字符串进行了处理，是一种能够高效存储和查找字符串集合的数据结构。

具体如下：

(图片来自一位大佬）

这段代码是一个简单的字典树（Trie）实现，用于处理字符串的插入和查询操作。下面是对每个部分的详细解释：

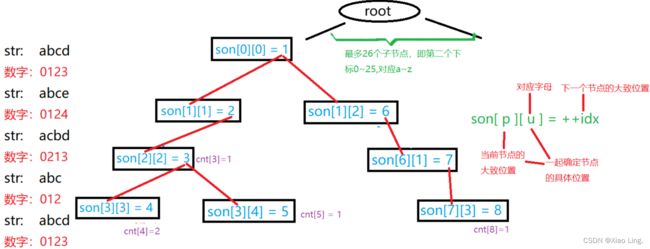
1. 全局变量定义：
   • int son[N][26]：这是字典树的主要数据结构，son[i][j]表示节点i的第j个子节点的编号。
   • int cnt[N]：cnt[i]表示以节点i为结束的字符串的数量。
   • int idx：用于给字典树中的每个节点分配一个唯一的编号。
   • char str[N]：用于存储输入的字符串。
2. 插入函数 void insert(char* str)：
   • 这个函数用于将一个字符串插入到字典树中。
   • 它首先将当前节点p设置为根节点（编号为0）。
   • 然后，对于字符串中的每个字符，它将字符转换为一个介于0和25之间的整数（通过减去’a’），然后检查当前节点是否有一个对应的子节点。如果没有，它就创建一个新的子节点，并更新son[p][u]和idx。
   • 最后，它将p移动到新的子节点，并在字符串结束时增加cnt[p]。
3. 查询函数 int query(char* str)：
   • 这个函数用于查询一个字符串在字典树中出现的次数。
   • 它的工作方式类似于插入函数，但是当它在查找子节点时，如果发现子节点不存在，它会立即返回0。
   • 如果字符串存在，它会返回cnt[p]，即以查询字符串结束的字符串的数量。
4. 主函数 int main()：
   • 首先，它读取一个整数m，表示操作的数量。
   • 然后，对于每个操作，它读取一个字符op和一个字符串str。如果op是’I’，它就调用insert(str)；否则，它就调用query(str)并打印结果。

这个代码的主要用途是处理大量的字符串插入和查询操作，特别是当字符串的长度和数量都可能非常大时。字典树是一种高效的数据结构，可以在这种情况下提供快速的插入和查询操作。这个代码可能用于处理一些需要大量字符串匹配的问题，例如文本搜索、词频统计等。