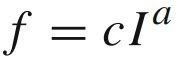【智能优化算法】蝴蝶优化算法-BOA
目录
前言
算法原理
条件假设
香味
蝴蝶自然行为的数学模型
优缺点
伪代码
算法优化
改进的蝴蝶优化算法
编码方法
评价函数
重新定义迭代公式
轮盘赌选择
交叉操作
变异操作编辑
IBOA实施步骤
编辑
实验分析
实验环境与参数设置
测试实例结果比较
结论
参考文献编辑
代码
MATLAB
前言
蝴蝶优化算法(butterfly optimization algorithm, BOA)是Arora 等人于2019年提出的一种元启发式智能算法。该算法受到了蝴蝶觅食和交配行为的启发,蝴蝶接收/感知并分析空气中的气味,以确定食物来源/交配伙伴的潜在方向。
蝴蝶利用它们的嗅觉、视觉、味觉、触觉和听觉来寻找食物和伴侣,这些感觉也有助于它们从一个地方迁徙到另一个地方,逃离捕食者并在合适的地方产卵。在所有感觉中,嗅觉是最重要的,它帮助蝴蝶寻找食物(通常是花蜜)。蝴蝶的嗅觉感受器分散在蝴蝶的身体部位,如触角、腿、触须等。这些感受器实际上是蝴蝶体表的神经细胞,被称为化学感受器。它引导蝴蝶寻找最佳的交配对象,以延续强大的遗传基因。雄性蝴蝶能够通过信息素识别雌性蝴蝶,信息素是雌性蝴蝶发出的气味分泌物,会引起特定的反应。
通过观察,发现蝴蝶对这些来源的位置有非常准确的判断。此外,它们可以辨识出不同的香味,并感知它们的强度。蝴蝶会产生与其适应度相关的某种强度的香味,即当蝴蝶从一个位置移动到另一个位置时,它的适应度会相应地变化。当蝴蝶感觉到另一只蝴蝶在这个区域散发出更多的香味时,就会去靠近,这个阶段被称为全局搜索。另外一种情况,当蝴蝶不能感知大于它自己的香味时,它会随机移动,这个阶段称为局部搜索。
算法原理
条件假设
蝴蝶的觅食、交尾
蝴蝶优化算法是模拟蝴蝶的觅食行为, 该思想的条件假设如下:
1) 所有的蝴蝶都应该散发出某种香味, 使蝴蝶能够互相吸引.
2) 每只蝴蝶都会随机移动, 或朝着散发出更多香味的最佳蝴蝶移动.
3) 蝴蝶的刺激强度受目标函数值的影响或决定.
当蝴蝶能感觉到其他任何蝴蝶的香味时并朝它移动, 在该算法中, 该阶段称为全局搜索. 在另一种情况下, 当蝴蝶不能感觉周围的香味时, 然后它会随机移动这个阶段称为局部搜索. 利用转换概率 控制全局和局部搜索过程, 其迭代公式为:
基于上述描述, 蝴蝶优化算法的实施步骤如下:
香味
为了理解算法中“香味”是如何定义的,我们首先要理解气味、声音、光、温度等模态是如何引入算法的。原文中提出了三个名词:感觉模态c、刺激强度I 和幂指数a。在蝴蝶的感觉模态中,感觉意味着判断模态的形式并以类似方式对其进行处理,这里的“模态”是指能量的输入。模态的形态可以是气味,声音,光线,温度,但就BOA而言,模态对应的是香味。I 是物理刺激的大小,其与蝴蝶的适应度相关。那么这就好理解了,当一只蝴蝶散发出的香味更浓(适应度值更优)时,周围的其他蝴蝶可以感知并被其吸引。幂指数a 是强度增加的指数,其可以为正则表达式、线性响应和响应压缩:
a.响应扩展: 当I 增加时,香味(f )比I 增长更快;
b.响应压缩: 当I 增加时,f 比I 增长慢;
c.线性响应: 当I 增加时,f 成比例地增加。
经实验证明,有时随着刺激的增强,昆虫对刺激变化的敏感性变得越来越低,也就是产生了抗性。因此为了估计I 的大小,在BOA中使用了响应压缩。
蝴蝶的自然行为主要基于两个点:I 的变化和f 的表示。l 与适应度的变化有关;f 是相对的,应该由蝴蝶相互之间感知而得。原文提到,当I 较弱的蝴蝶向I 较强的蝴蝶移动时,f 比I 增加得更快。因此,香味被表示为刺激物强度的函数:
其中c、a 为[0,1]内一随机值;a=1这种极端情况意味着一只蝴蝶发出的香味浓度会被其他蝴蝶以同样的能力感知,这相当于香味是在理想化的环境中传播,因此可以很容易地达到全局最优值;若a=0,这意味着任何一只蝴蝶散发出的香味都不会被其他蝴蝶感觉到,也就不存在“吸引”这个概念了。原文中将c 设为0.01,a 设为0.1。
蝴蝶自然行为的数学模型
结合前文内容,将蝴蝶的上述特征理想化:
a.所有的蝴蝶都可以发出气味,这使得蝴蝶间可以相互吸引。
b.每只蝴蝶都会随机移动或朝更香的蝴蝶移动,进而散发出更多的芳香。
c. 蝴蝶的刺激强度受目标函数的影响或决定。
在全局搜索阶段,蝴蝶向更香的蝴蝶移动:
其中,g∗表示在当前最优解,r 是[0,1]内一随机数。局部搜索阶段可以表示为:
其中,xj、xk为解空间中的两个随机个体。在算法中,蝴蝶寻找食物、交尾可以在局部和全局范围内发生。因此,BOA中使用切换概率p 以在全局搜索和局部搜索之间进行切换,p 通常为0.8。
优缺点
BOF 算法调节参数少,原理简单,易于实现,与常见的群智能优化算法一样容易陷入局部最优,后期迭代收敛速度较慢的特点。
伪代码
算法优化
参考郑洪清. 改进的蝴蝶优化聚类算法的论文
改进的蝴蝶优化算法
由于基本的BOA算法聚类效果差, 本文对其进行改进, 提出一种改进的蝴蝶优化聚类算法. 重新定义蝴蝶的局部搜索方式, 同时结合轮盘赌选择、交叉操作和变异操作, 提高算法的寻优能力, 使聚类效果稳定.
编码方法
评价函数
重新定义迭代公式
轮盘赌选择
交叉操作
变异操作
IBOA实施步骤
实验分析
实验环境与参数设置
为了测试IBOA算法的正确性与有效性, 选取6个基准测试函数来验证算法, 包括1个人工数据集和5个从UCI ( http://archive.ics.uci.edu/ml/index.php)数据库中选取了Iris、Wine、Glass、Cancer、Cintraceptive Method Choice (简称CMC) 5组实验数据, 所有的实例均运行在处理器为Celeron(R)双核CPU T3100, 1.90 GHz、内存为4G的PC上, 以Matlab R2010a编写代码. 参数设置为: 种群规模 =50、转换概率 =0.1、c的初值为0.01, 迭代次数N_iter=200和交叉概率pc=0.85. 在问题规模一致的情形下, 这些算法的复杂度是相同的.
测试实例结果比较
(1)人工数据集1 (set_data=250, d=3, K=5): 为了展示IBOA的求解过程, 分别计算第10代、第50代的求解结果如图1和图2中. 并将算法独立运行20次的结果于表1中, Best表示最优解, Average表示平均解, Worst表示最差解, Std表示标准差.表1中其他算法与数据来源于文献[7], 从表1中的计算结果可知IBOA的求解精度及鲁棒性均优于其他算法.
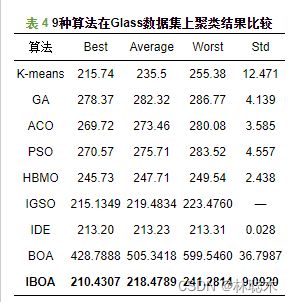
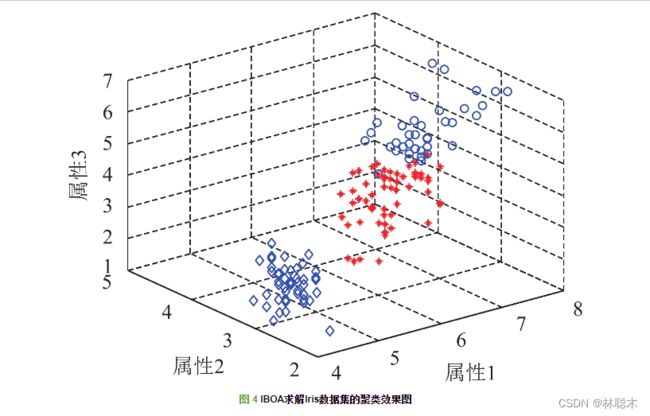
(2)UCI数据集: 将算法独立运行20次, 与近几年多种算法比较如表2–表7所示, 其中表2–表6中的K-means、GA、ACO、PSO、HBMO、IDE算法数据来源于文献[3]且迭代次数为500时的计算结果, IBA算法数据来源于文献[7], IGSO算法数据来源于文献[2], BPFPA算法数据来源于文献[6]; 表7中K-means、PSO、ABC、BA和IBA算法数据来源于文献[7]. 从表2可知, IBOA算法求解效果与IBA、BPFPA相当, 但比其余8种算法效果较好; 从表3可知, IBOA算法与BPFPA求解效果相当, 但比其余7种算法效果优越许多; 文中的“-”表示未有相关数据. 从表4可知, IBOA的求结果在迭代次数为200时优于IDE和其他算法; 从表5可知, IBOA算法的精度和方差均优于其他算法; 从表6可知, IBOA算法的求解效果差于IDE, 与IBA、BPFPA效果相当, 但优于其他算法; 从表7可知, IBOA算法的求解效果与IBA、BPFPA相当, 但优于其他算法. 另外, 图3展示了IBOA算法和BOA算法在Survival数据集的最优解收敛曲线图, 从图3易知, IBOA算法的求解速度和精度较BOA算法高.IBOA求解Iris、Survival、CMC数据集的聚类效果图如图4–图6所示.
结论
将精英策略的思想重新定义蝴蝶优化算法的局部搜索迭代公式且遗传算法相结合提出了一种改进的蝴蝶优化聚类算法, 通过求解1个人工数据集和5个UCI数据库中不同规模的数据, 统计分析结果表明IBOA算法能够避免陷入局部最优, 具有较快的收敛速度和较强的鲁棒性, 能够有效解决聚类问题且与其他聚类算法相比具有一定优势.
参考文献
代码
MATLAB
BOA
-
function [fmin,best_pos,Convergence_curve]
=BOA(n,N_iter,Lb,Ub,dim,fobj)
-
-
% n
is the population
size
-
% N_iter represnets total
number
of iterations
-
p
=
0.8; % probabibility switch
-
power_exponent
=
0.1;
-
sensory_modality
=
0.01;
-
-
%
Initialize the positions
of
search agents
-
Sol
=initialization(n,dim,Ub,Lb);
-
-
for i
=
1:n,
-
Fitness(i)
=fobj(Sol(i,:));
-
end
-
-
% Find the current best_pos
-
[fmin,I]
=min(Fitness);
-
best_pos
=Sol(I,:);
-
S
=Sol;
-
-
%
Start the iterations -- Butterfly Optimization Algorithm
-
for t
=
1:N_iter,
-
-
for i
=
1:n, % Loop over
all butterflies
/solutions
-
-
%Calculate fragrance
of each butterfly which
is correlated
with objective
function
-
Fnew
=fobj(S(i,:));
-
FP
=(sensory_modality
*(Fnew^power_exponent));
-
-
%
Global
or local
search
-
if rand
<p,
-
dis
= rand
* rand
* best_pos
- Sol(i,:); %Eq. (
2)
in paper
-
S(i,:)
=Sol(i,:)
+dis
*FP;
-
else
-
% Find
random butterflies
in the neighbourhood
-
epsilon
=rand;
-
JK
=randperm(n);
-
dis
=epsilon
*epsilon
*Sol(JK(
1),:)-Sol(JK(
2),:);
-
S(i,:)
=Sol(i,:)
+dis
*FP; %Eq. (
3)
in paper
-
end
-
-
% Check
if the simple
limits
/bounds
are OK
-
S(i,:)
=simplebounds(S(i,:),Lb,Ub);
-
-
%
Evaluate new solutions
-
Fnew
=fobj(S(i,:)); %Fnew represents new fitness
values
-
-
%
If fitness improves (better solutions found), update
then
-
if (Fnew
<=Fitness(i)),
-
Sol(i,:)
=S(i,:);
-
Fitness(i)
=Fnew;
-
end
-
-
% Update the current
global best_pos
-
if Fnew
<=fmin,
-
best_pos
=S(i,:);
-
fmin
=Fnew;
-
end
-
end
-
-
Convergence_curve(t,
1)
=fmin;
-
-
%Update sensory_modality
-
sensory_modality
=sensory_modality_NEW(sensory_modality, N_iter);
-
end
-
-
% Boundary constraints
-
function s
=simplebounds(s,Lb,Ub)
-
% Apply the lower bound
-
ns_tmp
=s;
-
I
=ns_tmp
<Lb;
-
ns_tmp(I)
=Lb;
-
-
% Apply the upper bounds
-
J
=ns_tmp
>Ub;
-
ns_tmp(J)
=Ub;
-
% Update this new
move
-
s
=ns_tmp;
-
-
-
function y
=sensory_modality_NEW(x,Ngen)
-
y
=x
+(
0.025
/(x
*Ngen));
-
-
-
Get_Functions_details
-
% lb
is the lower bound
-
%
up
is the uppper bound
-
% dim
is the
number
of variables
-
function [lb,ub,dim,fobj]
=
Get_Functions_details(F)
-
-
switch F
-
case
'F1'
-
fobj
= @F
1;
-
lb
=-
100;
-
ub
=
100;
-
dim
=
30;
-
end
-
-
end
-
-
function o
= F
1(x)
-
o
=
sum(x.^
2);
-
end
-
-
initialization
-
% This
function randomly initializes the position
of agents
in the
search
space.
-
function [X]
=initialization(N,dim,
up,
down)
-
-
if
size(
up,
1)
=
=
1
-
X
=rand(N,dim).
*(up-down)
+
down;
-
end
-
if
size(
up,
1)
>
1
-
for i
=
1:dim
-
high
=
up(i);low
=
down(i);
-
X(:,i)
=rand(
1,N).
*(high-low)
+low;
-
end
-
end
main
-
% Main paper: Sankalap Arora, Satvir Singh %
-
% Butterfly optimization algorithm: a novel approach
for
global optimization %
-
% Soft Computing %
-
% DOI: https:
/
/doi.org
/
10.1007
/s
00500-
018-
3102-
4 %
-
%___________________________________________________________________________________________ %
-
clear
all
-
clc
-
warning
off
all
-
-
SearchAgents_
no
=
30; %
Number
of
search agents
-
Max_iteration
=
500; % Maximum
number
of iterations
-
-
Function_name
=
'F1';
-
-
[lb,ub,dim,fobj]
=
Get_Functions_details(
Function_name);
-
-
[Best_score,Best_pos,cg_curve]
=BOA(SearchAgents_
no,Max_iteration,lb,ub,dim,fobj);
-
-
semilogy(cg_curve,
'Color',
'r')
-
title(
'Convergence curve')
-
xlabel(
'Iteration');
-
ylabel(
'Best score obtained so far');
-
-
axis tight
-
grid
off
-
box
on
-
legend(
'BOA')
-
-
display([
'The best solution obtained by BOA is : ', num
2str(Best_pos)]);
-
display([
'The best optimal value of the objective funciton found by BOA is : ', num
2str(Best_score)]);
-
-
Python
-
# -
*- coding: utf-
8 -
*-
-
-
import
time
-
import numpy
as np
-
from dramkit.gentools import isnull, power
-
from dramkit.optimizer.utils_heuristic import rand_init
-
-
-
def boa(objf, func_opter_parms):
-
''
'
-
蝴蝶优化算法(Butterfly Optimization Algorithm) BOA
-
TODO
-
----
-
目前仅考虑自变量连续实数情况,以后可增加自变量为离散的情况
-
Parameters
-
----------
-
objf : function
-
目标函数。注:须事先转化为求极小值问题
-
func_opter_parms : FuncOpterInfo
-
:class:`dramkit.optimizer.utils_heuristic.FuncOpterInfo` 类,
-
须设置parms_func、parms_opter、parms_log
-
| parms_func为目标函数参数信息dict,key须包含:
-
| x_lb: 自变量每个维度取值下界,list或数值,为list时长度应等于dim
-
| x_ub: 自变量每个维度取值上界,list或数值,为list时长度应等于dim
-
| dim: 自变量维度数
-
| kwargs: 目标函数接收的其它参数
-
| parms_opter: 优化函数参数信息dict,key须包含:
-
| popsize: 群体数量(每轮迭代的样本数量)
-
| max_iter: 最大迭代寻优次数
-
| p: 全局/局部搜索转化概率
-
| power_exponent: `a` in BOA蝴蝶优化算法.pdf-Eq.(1)
-
| sensory_modality: `c` in BOA蝴蝶优化算法.pdf-Eq.(1)
-
| parms_log: 日志参数信息dict,key须包含:
-
| logger: 日志记录器
-
| nshow: 若为整数,则每隔nshow轮日志输出当前最优目标函数值
-
Returns
-
-------
-
func_opter_parms : FuncOpterInfo
-
更新优化过程之后的func_opter_parms
-
References
-
----------
-
- BOA蝴蝶优化算法.pdf
-
'
''
-
-
# 参数提取
-
opter_name
= func_opter_parms.parms_opter[
'opter_name']
-
if opter_name
=
=
''
or isnull(opter_name):
-
opter_name
=
'boa'
-
func_opter_parms.parms_opter[
'opter_name']
= opter_name
-
# 目标函数参数
-
x_lb
= func_opter_parms.parms_func[
'x_lb']
-
x_ub
= func_opter_parms.parms_func[
'x_ub']
-
dim
= func_opter_parms.parms_func[
'dim']
-
kwargs
= func_opter_parms.parms_func[
'kwargs']
-
# 优化器参数
-
popsize
= func_opter_parms.parms_opter[
'popsize']
-
max_iter
= func_opter_parms.parms_opter[
'max_iter']
-
p
= func_opter_parms.parms_opter[
'p']
-
power_exponent
= func_opter_parms.parms_opter[
'power_exponent']
-
sensory_modality
= func_opter_parms.parms_opter[
'power_exponent']
-
# 日志参数
-
logger
= func_opter_parms.parms_log[
'logger']
-
nshow
= func_opter_parms.parms_log[
'nshow']
-
-
# 时间记录
-
strt_tm
=
time.
time()
-
func_opter_parms.
set_
start_
time(
time.strftime(
'%Y-%m-%d %H:%M:%S'))
-
-
-
# 边界统一为列表
-
if
not isinstance(x_lb, list):
-
x_lb
= [x_lb]
* dim
-
if
not isinstance(x_ub, list):
-
x_ub
= [x_ub]
* dim
-
-
-
# 初始化所有个体|样本
-
Xall
= rand_init(popsize, dim, x_lb, x_ub)
-
-
# 保存收敛过程
-
convergence_curve
= np.
zeros(max_iter) # 全局最优值
-
convergence_curve_mean
= np.
zeros(max_iter) # 平均值
-
-
# 初始函数值
-
fvals
= np.
zeros(popsize)
-
for k
in range(popsize):
-
fvals[k]
= objf(Xall[k, :],
**kwargs)
-
best_idx
= fvals.argmin()
-
best_y
= fvals[best_idx]
-
best_x
= Xall[best_idx]
-
-
S
= Xall.
copy()
-
-
-
def sensory_modality_new(x, Ngen):
-
y
= x
+ (
0.025
/ (x
*Ngen))
-
return y
-
-
-
# 迭代寻优
-
for t
in range(
1, max_iter
+
1):
-
fvals_mean
=
0 # 记录每代目标函数均值
-
for i
in range(
1, popsize
+
1):
-
fval
= objf(S[i-
1, :],
**kwargs)
-
FP
= sensory_modality
* power(fval, power_exponent)
-
-
# 全局|局部搜索
-
r
1, r
2
= np.
random.rand(), np.
random.rand()
-
if np.
random.rand()
< p:
-
# BOA蝴蝶优化算法.pdf-Eq.(
2)
-
# dis
= r
1
* r
1
* best_x
- Xall[i-
1, :]
-
dis
= r
1
* r
2
* best_x
- Xall[i-
1, :]
-
S[i-
1, :]
= Xall[i-
1, :]
+ dis
* FP
-
else:
-
# BOA蝴蝶优化算法.pdf-Eq.(
3)
-
JK
= np.
random.permutation(popsize)
-
dis
= r
1
* r
1
* Xall[JK[
0], :]
- Xall[JK[
1], :]
-
# dis
= r
1
* r
2
* Xall[JK[
0], :]
- Xall[JK[
1], :]
-
S[i-
1, :]
= Xall[i-
1, :]
+ dis
* FP
-
-
# 越界处理
-
S[i-
1, :]
= np.clip(S[i-
1, :], x_lb, x_ub)
-
-
-
# 最优值和最优解更新
-
fval
= objf(S[i-
1, :],
**kwargs)
-
if fval
<= best_y:
-
best_x
= S[i-
1, :].
copy()
-
best_y
= fval
-
-
if fval
<= fvals[i-
1]:
-
Xall[i-
1, :]
= S[i-
1, :].
copy()
-
fvals[i-
1]
= fval
-
-
fvals_mean
= (fvals_mean
*(i-
1)
+ fval)
/ i
-
-
# Update sensory_modality
-
sensory_modality
= sensory_modality_new(sensory_modality, max_iter)
-
-
# 每轮迭代都保存最优目标值
-
convergence_curve[t-
1]
= best_y
-
convergence_curve_mean[t-
1]
= fvals_mean
-
-
if nshow:
-
if t % nshow
=
=
0:
-
opter_name
= func_opter_parms.parms_opter[
'opter_name']
-
func_name
= func_opter_parms.parms_func[
'func_name']
-
logger.info(
'{} for {}, iter: {}, '.
format(opter_name, func_name, t)
+ \
-
'best fval: {}'.
format(best_y))
-
-
-
# 更新func_opter_parms
-
end_tm
=
time.
time()
-
func_opter_parms.
set_
end_
time(
time.strftime(
'%Y-%m-%d %H:%M:%S'))
-
func_opter_parms.
set_exe_
time(
end_tm-strt_tm)
-
func_opter_parms.
set_convergence_curve(convergence_curve)
-
func_opter_parms.
set_convergence_curve_mean(convergence_curve_mean)
-
func_opter_parms.
set_best_val(best_y)
-
func_opter_parms.
set_best_x(best_x)
-
-
return func_opter_parms
-
-
-
if __name__
=
=
'__main__':
-
import pandas
as pd
-
from dramkit.optimizer.base_funcs import TestFuncs
-
from dramkit.optimizer.utils_heuristic import FuncOpterInfo
-
from dramkit import plot_series, simple_logger
-
from dramkit.logtools.logger_general import
get_logger
-
from dramkit.logtools.utils_logger import
close_log_
file
-
-
-
strt_tm
=
time.
time()
-
-
objf
= TestFuncs.f
11
-
parms_func
= {
'func_name': objf.__name__,
-
'x_lb': -
10,
'x_ub':
10,
'dim':
10,
'kwargs': {}}
-
parms_opter
= {
'opter_name':
'boa-test',
-
'popsize':
30,
'max_iter':
500,
-
'p':
0.6,
'power_exponent':
0.1,
'sensory_modality':
0.01}
-
# logger
= simple_logger()
-
logger
=
get_logger(
'./_test/log/boa_test.txt',
screen_show
=
True)
-
# parms_log
= {
'logger': logger,
'nshow':
10}
-
parms_log
= {
'logger': logger,
'nshow':
100}
-
-
func_opter_parms
= FuncOpterInfo(parms_func, parms_opter, parms_log)
-
func_opter_parms
= boa(objf, func_opter_parms)
-
-
vals
= pd.DataFrame({
'fval_best': func_opter_parms.convergence_curve,
-
'fval_mean': func_opter_parms.convergence_curve_mean})
-
plot_series(vals, {
'fval_best':
'-r',
'fval_mean':
'-b'}, figsize
=(
10,
6))
-
-
best_x
= func_opter_parms.best_x
-
func_opter_parms.parms_log[
'logger'].info(
'best x: {}'.
format(best_x))
-
-
close_log_
file(logger)
-
-
-
print(
'used time: {}s.'.
format(round(
time.
time()-strt_tm,
6)))