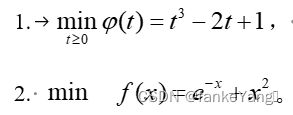0.618算法和基于Armijo准则的线搜索回退法
0.618代码如下:
import math
# 定义函数h(t) = t^3 - 2t + 1
def h(t):
return t**3 - 2*t + 1
# 0.618算法
def golden_section_search(a, b, epsilon):
ratio = 0.618
while (b - a) > epsilon:
x1 = b - ratio * (b - a)
x2 = a + ratio * (b - a)
h_x1 = h(x1)
h_x2 = h(x2)
if h_x1 < h_x2:
b = x2
else:
a = x1
return a # 或者返回 b,因为它们的值非常接近
# 在 t 大于等于 0 的范围内进行搜索
t_min_618 = golden_section_search(0, 3, 0.001)
print("0.618算法找到的最小值:", h(t_min_618))
基于Armijo准则的线搜索回退法代码如下:
import numpy as np
def h(t):
return t**3 - 2*t + 1
def h_derivative(t):
return 3*t**2 - 2
def armijo_line_search(t_current, direction, alpha, beta, c1):
t = t_current
step_size = 1.0
while True:
if h(t + direction * step_size) <= h(t) + alpha * step_size * direction * h_derivative(t):
return t + direction * step_size
else:
step_size *= beta
if np.abs(step_size) < 1e-6:
break
return None
def gradient_descent(start, end, alpha, beta, c1, epsilon):
t = start
while True:
if t > end:
break
direction = -h_derivative(t) # 负梯度方向
next_t = armijo_line_search(t, direction, alpha, beta, c1)
if next_t is None or np.abs(h_derivative(next_t)) <= epsilon:
return next_t
t = next_t
return None
# 参数设置
alpha = 0.1 # Armijo准则中的参数alpha
beta = 0.5 # Armijo准则中的参数beta
c1 = 1e-4 # 自定义参数,用于控制Armijo条件的满足程度
epsilon = 1e-6 # 梯度范数的终止条件
# 搜索区间为[0,3]
start = 0
end = 3
# 执行梯度下降算法,求得近似最小值点
t_min = gradient_descent(start, end, alpha, beta, c1, epsilon)
print("求得的最小值点为:", t_min)
print("最小值点的函数值为:", h(t_min))