FIR滤波器窗函数设计法——汉明窗设计实例

---

前言

数字滤波器按单位抽样响应的时间特性可分为无限长单位抽样响应数字（IIR）滤波器和有限长单位抽样响应数字（FIR）滤波器,其中的FIR相比于IIR，最大的优点为可实现线性相位。此外由于FIR滤波器的单位抽样响应为有限长，因此一定稳定且可由一因果系统来实现，本篇为本人之前的学习笔记，主要讨论窗函数法设计FIR滤波器（以汉明窗为例）。

一、FIR滤波器的设计方法

1 窗函数设计法的原理

FIR滤波器的设计方法主要有：窗函数法、频率抽样法、等波纹逼近法。
窗函数设计法的思想概述是：

用FIR数字滤波器去逼近所期望的理想滤波器特性，设理想滤波器的频率响应函数为$H_d\left(e^{jw}\right)$,对应的单位抽样响应为$h_d\left(n\right)$,由于$h_d\left(n\right)$为理想滤波器，所以是无限长非因果序列,因此需要选择合适的窗函数$w_n$对其进行截取和加权处理，从而得到FIR数字滤波器的单位抽样函数$h(n)$。在设计过程中，窗函数的类型和长度都直接影响逼近精度，$h(n)$也应满足线性相位约束条件。

以上是课本上对设计原理的描述，接下来用简单易懂的语言解释一下，在解释之前首先要回忆起：理想滤波器也就是在信号与系统中所提及的理想低通，理想高通，理想带通，理想带阻等。（下面开始解释）这些滤波器有一个共同特点，就是边沿特性极为理想，如一个理想窗函数其傅里叶反变换为$Sa$函数，在时域上是无限宽，为非因果系统，非因果系统有一个致命的弊端，那就是在物理上不可实现。而为了解决这一弊端所采用的方法就是加窗，这就需要引入接下来几种典型窗函数。

2 窗函数的主要指标和设计方法

典型的窗函数有：矩形窗，巴特利特窗，汉宁窗，汉明窗，布莱克曼窗，凯塞窗。

窗函数的主要指标有：
最大旁瓣峰值${\delta }_n\left(dB\right)$：窗函数幅频响应函数取对数后的值，单位为分贝。
主瓣宽度${\omega }_{main}$：指窗函数频谱的主瓣宽度。
过渡带宽$\Delta \omega$：指FIR滤波器的过渡带宽，即通带截止频率与阻带截止频率之差。
阻带最小衰减:${\delta }_{st}\left(dB\right)$:用该窗函数设计得到的FIR滤波器的阻带最小衰减。
在设计时的原则为：应使主瓣尽可能窄，以获得较陡的过渡带宽；最大旁瓣相对于主瓣应尽可能小，即能量尽可能集中在主瓣（阻带衰减尽可能大）。
事实上，以上两原则无法同时实现，在设计时常常取两要求的折衷。

3 汉明窗的特性和设计方法

汉明窗又称改进的升余弦窗，可使得旁瓣比升余弦窗（汉宁窗）更小，其时域定义式为：$$w(n)=\left[0.54-0.46\cos \left(\frac{2\pi n}{N-1}\right)\right]R_N(n)$$
傅里叶变换和对应窗谱分别为：
$$\begin{array}{rl}& W\left(e^{j\omega }\right)=\left\{0.54R_N(\omega )+0.23\left[R_N\left(\omega -\frac{2\pi }{N-1}\right)+R_N\left(\omega +\frac{2\pi }{N-1}\right)\right]\right\}{e}^{-j\frac{N-1}{2}\omega }\\ & =W(\omega )e^{-j\frac{N-1}{2}\omega }\\ & W(\omega )=0.54R_N(\omega )+0.23\left[R_N\left(\omega -\frac{2\pi }{N-1}\right)+R_N\left(\omega +\frac{2\pi }{N-1}\right)\right]\end{array}$$
结论：当长度相同时，三角窗，汉宁窗和汉明窗的主瓣宽度均为$\frac{8\pi }{N}$,且汉明窗的旁瓣最低

二、汉明窗设计滤波器实例

采用窗函数法设计FIR滤波器的步骤已于上文中提及，这里不做赘述，在根据设计要求选择最优窗函数时这里默认选择汉明窗。

1.低通滤波器matlab示例

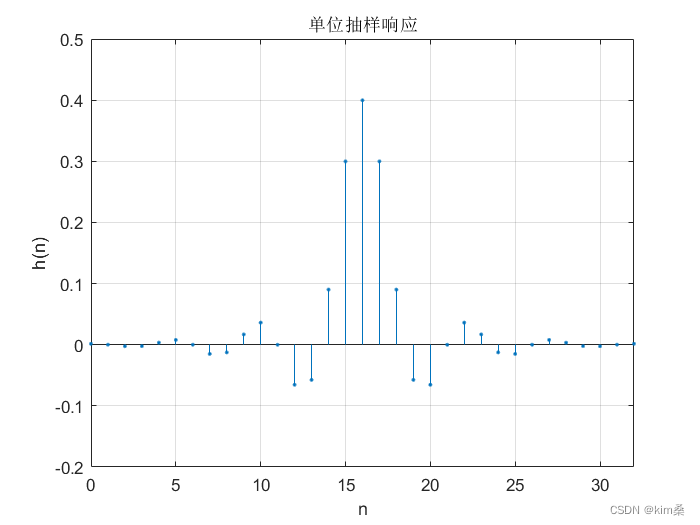
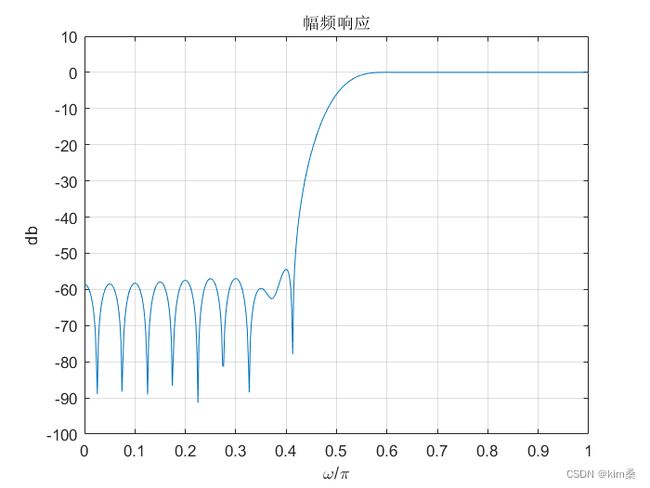
本例实现用汉明窗设计一个FIR低通滤波器，通带截止频率${\omega }_p$=0.3$\pi$，阻带截止频率为${\omega }_{st}=0.5\pi$。

 wp=0.3;
 ws=0.5；
 wc=(wp+ws)/2;
 delta_w=ws-wp;
 N=ceil(6.6/delta_w)；
 hn=fir1(N-1,wc,'low',hamming(N));
 omega=linspace(0,pi,512);
 mag=freqz(hn,1,omega);
 magdb=20*log10(abs(mag));
 stem([0:N-1],hn,'.');
 grid on;
 axis([0 N-1 -0.2 0.5]);
 xlabel('n');
 ylabel('h(n)');title('单位抽样响应');
  plot(omega/pi,magdb);
 grid on;
 axis([0 1 -100 10]);
 xlabel('\omega/\pi');
 ylabel('db');title('幅频响应');

在程序中需要注意的是Matlab所提供的库函数fir1，其应用格式为：

hn=fir1(N,wc,ftype,win)

其中N为滤波器的阶数（滤波器长度为N+1）,wc为6dB截止频率，ftype为滤波器类型，win为所用窗函数类型。ftype可选择低通（low），高通(high)，带通(bandpass)，带阻(stop)，若省略则默认为低通，当选择带通或带阻时wc=[wc1,wc2]，表示上/下截止频率，win表示窗的类型，若省略则默认为汉明窗。
fir1还可以设计成多通带滤波器格式如

h=fir1(N,wc,'DC-1')
或者
h=fir1(N,wc,'DC-0')

前者表示从通带开始，后者表示从阻带开始。

2.高通滤波器matlab示例

 wc=0.5;
 alpha=20;
 N=2*alpha+1;
 hn=fir1(N-1,wc,'high',hamming(N))
 omega=linspace(0,pi,512);
 mag=freqz(hn,1,omega);
 magdb=20*log10(abs(mag));
 stem([0:N-1],hn,'.');
 grid on;
 axis([0 N-1 -0.2 0.5]);
 xlabel('n');
 ylabel('h(n)');title('单位抽样响应');
  plot(omega/pi,magdb);
 grid on;
 axis([0 1 -100 10]);
 xlabel('\omega/\pi');
 ylabel('db');title('幅频响应');

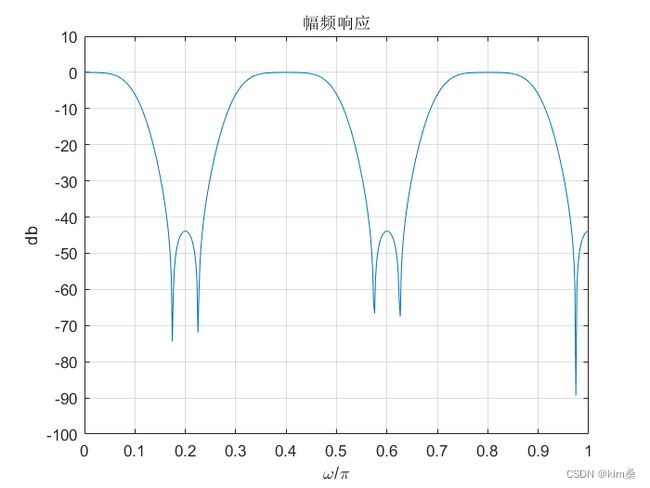
3.多通带滤波器matlab示例

 wc=[0.1 0.3 0.5 0.7 0.9];
 N=51;
 hn=fir1(N-1,wc,'DC-1',hamming(N));
 omega=linspace(0,pi,512);
 mag=freqz(hn,1,omega);
 magdb=20*log10(abs(mag));
 stem([0:N-1],hn,'.');
 grid on;
 axis([0 N-1 -0.2 0.5]);
 xlabel('n');
 ylabel('h(n)');title('单位抽样响应');
 plot(omega/pi,magdb);
 grid on;
 axis([0 1 -100 10]);
 xlabel('\omega/\pi');
 ylabel('db');title('幅频响应');