DFS入门题--迷宫问题--详细--用于自我记录

本题目来源取自网络。
题目补充：只能走上下左右四个方向，不能斜向走；
输入（行m，列n，行列的数字，起点坐标，终点坐标）
5 4
1 1 2 1
1 1 1 1
1 1 2 1
1 2 1 1
1 1 1 2
1 1 4 3
输出：7
DFS简述：
“不到南墙不回头”，从当前点往下搜索，如果满足条件，标记满足点为搜索过，则以满足条件的点为起点继续搜索，直到不满足条件，则一直回退到与满足条件的点的相邻的，且未被搜索过的点，继续重复上述操作。
当然这只是我个人理解，更多以及更好的DFS原理详解，参考百度。

回溯的个人基本理解：
在DFS结束后，如果还想再次使用路径上的点作为新的路径中的一个点，则在DFS结束后，要将标记的点取标，以便于新端点的搜索。
题目分析：
dfs的基本判断
判断终止与进行条件：

• 当前格子不是空地 || 当前格子越界 则返回return；
• 当前格子是终点，执行对应语句块，return;
• 当前格子是空地 && 当前格子没被访问过 执行语句块XXXXX

假设从起点（1,1）出发，对起点的相应的四个方向进行搜索，现在规定以右方向为初始搜索方向，顺时针搜索：右->下->左->上
开始搜索的计算机思路（大白话）：
从(1,1)向右搜索，(1,2)为空地，满足搜索的条件，步长+1，则标记该点走过，同时以（1,2）为起点继续搜索；
从(1,2)向右搜索，(1,3)为障碍物，步长+1，不满足搜索的条件，则执行第一个终止条件中的语句，接着return。此时return回去的语句是以（1,2）为起点的搜索情况，结束的是以向右搜索的情况。按照一开始设定的搜索思路，顺时针搜索，接下来是向下搜索。
从(1,2)向下搜索，(2,2)为空地且未被访问过，满足搜索的条件，步长+1，则标记该点走过，同时以（2,2）为起点继续搜索；
从(2,2)向右搜索，(2,3)为空地且未被访问过，满足搜索的条件，步长+1，则标记该点走过，同时以（2,3）为起点继续搜索；
从(2,3)向右搜索，(2,4)为空地且未被访问过，满足搜索的条件，步长+1，则标记该点走过，同时以（2,4）为起点继续搜索；
从(2,4)向右搜索，(2,5)超出范围了，不满足搜索的条件，return到（2,4）搜索情况。
接着从(2,4)向下搜索，(3,4)为空地且未被访问过，满足搜索的条件，步长+1，则标记该点走过，同时以（3,4）为起点继续搜索；
从（3,4）开始搜索，向右，不成立，跳出，向下，成立，则标记，同时步数加1。
接着从（3，5）开始搜索，顺时针搜索到了终点，标记，步长+1；
此刻结束了的步长为7.
以上是一条路径的搜索的全过程。
接下来是讲回溯的过程。
那么到达终点以后，此刻对应的点都被标记，为了便于理解，我画了简图。
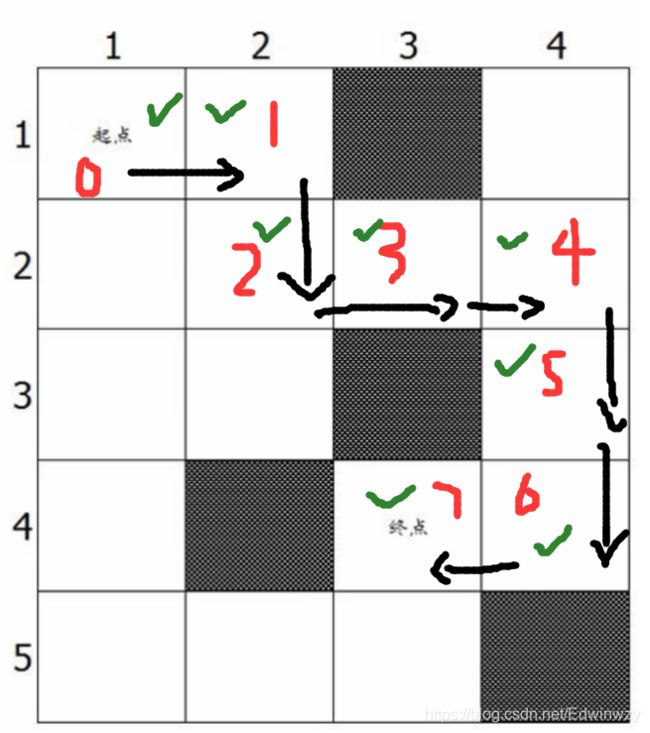绿色为标记，红色为步数，黑色为路径
那么接下来开始回溯：
从终点开始回溯，删除终点的标记点，返回到步长为6的点，继续以（4,4）为起点开始搜索，因为（4,4）到终点是向左搜索所以，按照顺时针的搜索方式，下一个点向上搜索，但是由于（3,4）已经标记过了，所以return。
这时候到了步长为5的点（3,4），因为（4,4）是（3,4）向下搜索的情况，返回后，继续顺时针搜索，则向右搜索，（3,3）是障碍物，所以return，接下来向上搜索，是
标记过的点，所以return到了（2,4）的搜索情况。
接下来依次这样执行直到（2,2）这个点搜索情况
下面是另外的路径情况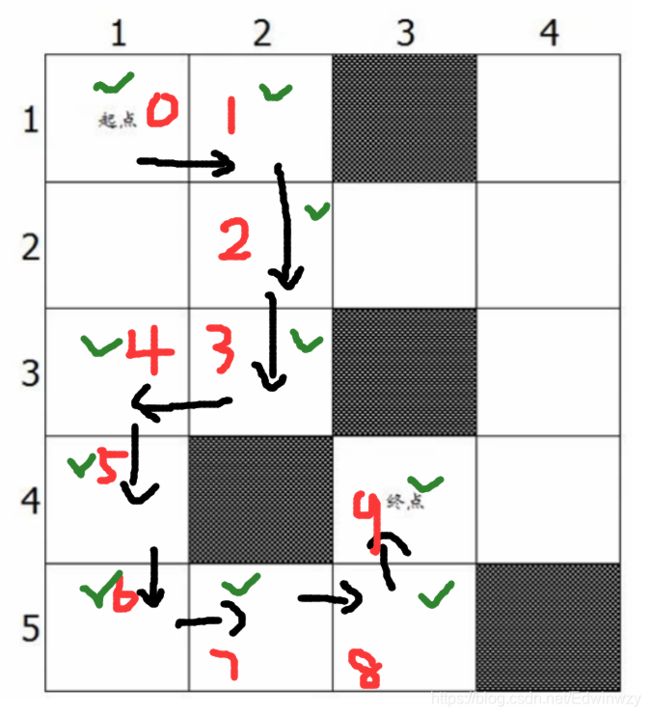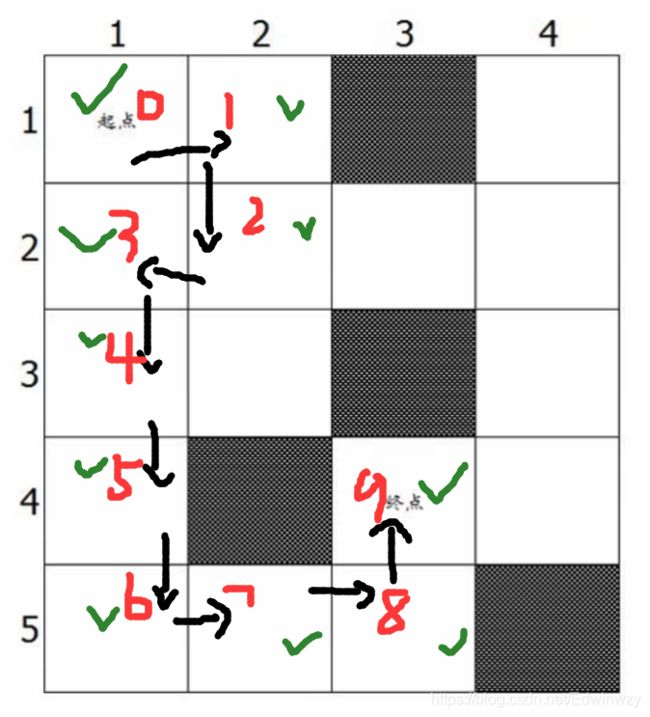其实到这里，题目已经差不多做完了。还需要对每条路径的长度进行比较，选出最短的进行输出，即为答案。
源代码如下：

#include
using namespace std;
int m,n,p,q,MIN=9999;//m为行，n为列，pq分别为终点xy坐标，MIN最短步数； 
int a[105][105]; //地图数组 
int visit[105][105];//访问数组，用来标记 
int dx[4]={0,1,0,-1};//对应的右下左上的x的位移 
int dy[4]={1,0,-1,0};//对应的右下左上的y的位移 
void dfs(int x,int y,int step)
{
	if (x<0||x>m||y<0||y>n||visit[x][y]==1)return ;//数组越界或者被标记了
	if(x==p && y==q)//如果是终点，判断当前路径的步数是否最小 
	{
		if(step<MIN)MIN=step;
		return ;
	}
	for(int i=0;i<4;i++)
	{
		int tx=x+dx[i];
		int ty=y+dy[i];
		if(a[tx][ty]==1&&visit[tx][ty]==0)
		{
			visit[tx][ty]=1;//标记当前搜索的点为已访问 
			dfs(tx,ty,++step);//以当前这个点为起点继续搜索 
			visit[tx][ty]=0;//搜索完以后，回溯，取消该点的访问。 
		}
	}
}
int main()
{
	int startx,starty;
	cin>>m>>n;
	for(int i=1;i<=m;i++)
	{
		for(int j=1;j<=n;j++)
		{
			cin>>a[i][j];
		}		
	}
	cin>>startx>>starty;//输入起点坐标 
	cin>>p>>q;//输入终点坐标 
	visit[startx][starty]=1;//起始位置标记走过 
	dfs(startx,starty,0);//从起点坐标开始搜索 
	cout<<MIN;
	return 0;
}

做了这题，是我的DFS真正的一次入门，写这篇博客，用来记录一下。如果对你们有帮助，欢迎一起学习。