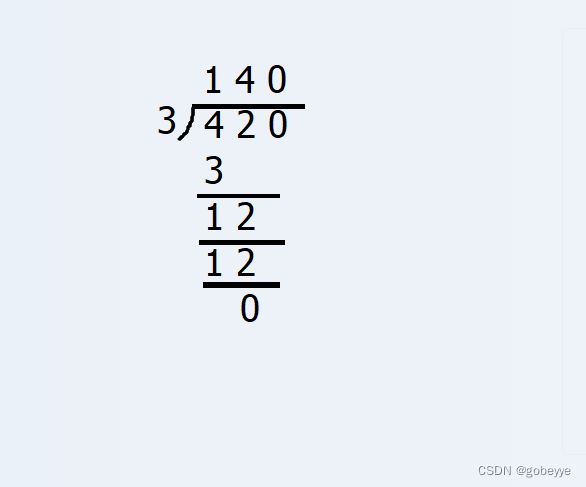算法之高精度模板（用函数实现c语言）有给出例题练手

前言：

在给出模板之前先简单介绍一下什么高精度（有了解的朋友此处可跳过）在c语言入门部分介绍了几种数据类型，并且每种数据类型容量是有限的，最大也就不过long long 那如果有的数连long long都存储不下该怎么办呢        我们可以用数组来模拟非常长的整数，用数组来完成四则运算。

介绍完概念后下面就给出高精度四则运算的模板，大家以后遇到类似的题可以直接用模板可以省去不少思考的时间，并且是用函数实现的可以多次调用，且主函数直接引用函数主函数看起来不会太乱，这也是我为什么要把模板写成函数。

下面的四个模板大体思路是

1.将字符串转成数字并反向存储。

2.进位

3.返回位数（我们用函数特有的）很方便的能加快程序的速度。

---

下面给出的例题均在洛谷（百度直接搜洛谷里面有个问题跳转） 里面能搜题号 （题号是p加数字）

加法：

解释写在代码里了，下面有些图片大家可以看看帮助理解。

#define  _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
int max(int x, int y)
{
	if (x >= y) return x;
	else return y;
}
int plas(char a[5005], char b[5005], int* su)
{
	int p1[5005] = { 0 };
	int p2[5005] = { 0 };
	int lena = strlen(a);//计算出a有几个数字
	int lenb = strlen(b);//计算出b有几个数字
	int i;
	int jw = 0;
	for (i = 0; i < lena; i++) p1[i] = a[lena - 1 - i] - '0';//将字符串转换成数字并反向存储
	for (i = 0; i < lenb; i++) p2[i] = b[lenb - 1 - i] - '0';
	int len = max(lena, lenb);//找出a和b的谁的数字多
	for (i = 0; i < len; i++)
	{
		su[i] = p1[i] + p2[i] + jw;//jw是用来进位
		jw = su[i] / 10;
		su[i] %= 10;
	}
	if (jw > 0)//特判当jw还有值（这个值是当前最高位的进位的数字）
	{
		su[len] = jw;
		len++;//用len来记入数子长度能省不少空间
	}
	return len;//这个函数返回两数相加的位数
}
int main()
{
	char a[5005];
	char b[5005];
	int sum[5005] = { 0 };//a+b的和
	scanf("%s", a);//输入数字a
	scanf("%s", b);//输入数字b
	int len = plas(a, b, sum);//plas函数就是高精度加法
	for (int i = len - 1; i >= 0; i--) printf("%d", sum[i]);//减去一位因为是从0开始的
	return 0;
}

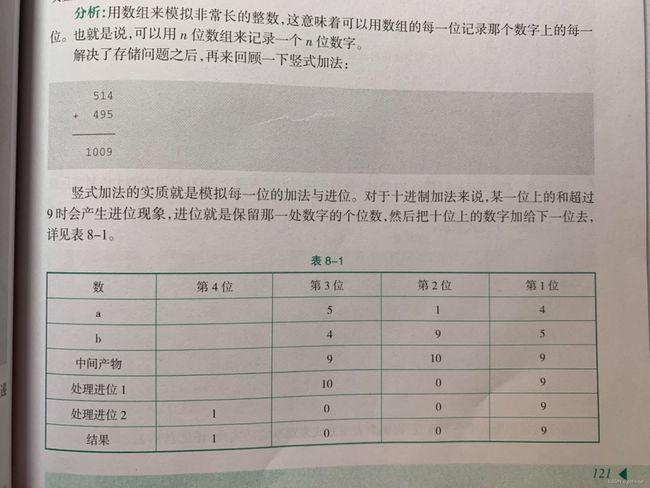
为什么要将数字逆向存储呢下面我给出一张图相信你就明白了

---

上面的图片重点看514和495的加法展示和下面的表8-1的进位说明，为什么不自己画图呢，因为我不会书上的图挺好的。

例题 洛谷 题号P1601 A+B Problem（高精）

写一遍会跟有感觉呢。

减法：

#define  _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
int pd = 0;//pd用来判断相减后是不是负数
int max(int x, int y)
{
	if (x >= y) return x;
	else return y;
}
int sub(char a[50000], char b[50000], int c[50000])
{
	int p1[50000] = { 0 };
	int p2[50000] = { 0 };
	int lena = strlen(a);
	int lenb = strlen(b);
	if (lenb > lena || (lenb == lena && strcmp(a, b) < 0))//是负数交换保证p1为大的数（方便运算）
	{
		pd = 1;
		char temp[50000];
		strcpy(temp, a);
		strcpy(a, b);
		strcpy(b, temp);
	}
	int i;
	int jw = 0;
	lena = strlen(a);
	lenb = strlen(b);
	for (i = 0; i < lena; i++) p1[i] = a[lena - 1 - i] - '0';
	for (i = 0; i < lenb; i++) p2[i] = b[lenb - 1 - i] - '0';
	int len = max(lena, lenb);
	for (i = 0; i < len; i++)
	{
		if (p2[i] > p1[i])//p1数不够去找高位借，保证不会出现负数
		{
			p1[i + 1] -= 1;
			p1[i] += 10;
		}
		c[i] = p1[i] - p2[i];
	}
	while (c[len] == 0 && len > 0) len--;//去零因为最高位可能变成0但是没有0454这样的数字故要把0去掉
	return len + 1;
}

int main()
{
	char a[50000];
	char b[50000];
	int  c[50000] = { 0 };
	scanf("%s", a);
	scanf("%s", b);
	int len = sub(a, b, c);
	if (pd == 1) printf("-");
	for (int i = len - 1; i >= 0; i--) printf("%d", c[i]);
	return 0;

}

---

和加法差不多多了一个特判输出符号的操作，加法是进位，减法是借位。

例题 洛谷 P2142 高精度减法

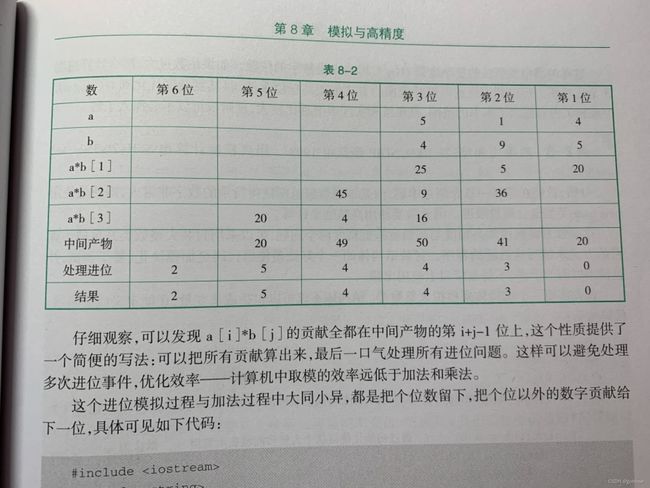
乘法：

#define  _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#include 
int ridess(char a[50000], char b[50000],char c[50000])
{
    int p1[50000] = { 0 }, p2[50000] = { 0 };
    int lena = strlen(a);
    int lenb = strlen(b);
    int i;
    int j;
    for (i = 0; i < lena; i++) p1[i] = a[lena - 1 - i] - '0';//翻转
    for (i = 0; i < lenb; i++) p2[i] = b[lenb - 1 - i] - '0';
    int jw = 0;
    int len = 0;
    for (i = 0; i < lena; i++)
    {
        for (j = 0; j < lenb; j++)
        {
            c[j + i] += p1[i] * p2[j] + jw;//jw用来进位
            jw = c[j + i] / 10;
            c[j + i] %= 10;
        }
        if (jw > 0)
        {
            c[i + j] = jw;//如果最后的值大于10那么还要在先更高位赋一位
            jw = 0;//最重要的一步卡了好久
        }
    }
    len = lena + lenb;
    while (c[len] == 0 && len > 0) len--;
    return len + 1;
}
int main()
{
    char a[50000], b[50000],c[50000];
    scanf("%s", a);
    scanf("%s", b);
    int len = ridess(a, b,c);
    int i;
    for (i = len - 1; i >= 0; i--) printf("%d", c[i]);
    return 0;
}

乘法过程如下图

---

例题 洛谷 P1303 A*B Problem

除法：

#define  _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#include 
int dic(char a[50005], long long b, long long c[50005])
{
	long long p[50005];
	int i;
	int lena = strlen(a);
	for (i = 0; i < lena; i++) p[i] = a[i] - '0';//除法和前面三个都不一样，不用倒叙存储和前面一样，大家可以在纸上谢谢除法的运算
	long long d = 0;
	for (i = 0; i < lena; i++)
	{
		c[i] = (d * 10 + p[i]) / b;//余数到下一位要乘10
		d = (d * 10 + p[i]) % b;//余数
	}
	int la = 0;
	while (c[la] == 0 && la < lena - 1)la++;//去掉前导0
	return la;
}
int main()
{
	char a[50005];
	long long b;
	long long c[50005];
	scanf("%s", a);
	scanf("%lld", &b);
	int f = dic(a, b, c);
	int i;
	int len = strlen(a);//为什么要小于len就行呢，大家可以自己试试，会发现去掉前导0，剩下的到len的数就是除数的位数后置0不能删去
	for (i = f; i < len; i++) printf("%lld", c[i]);
	return 0;
}

---

---

好好理解一下上面这张除法图结合一下我写在代码里的注释相信你就明白了。

例题 洛谷 P1480 A/BProblem

学习完上面的加减乘除后下面我给出一题大家可以自己去试试自己学习的答案在后面建议大家先自己完成在看答案，这样才会有收获。

练习 例题 P1009 [NOIP1998 普及组] 阶乘之和

题解如下：

#define  _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#include 
#include 
int ret[500005] = { 1 };
int sum[500005] = { 0 };
int i;
void cheng()
{
    int m;
    for (m = 0; m < 100; m++)
    {
        ret[m] *= i;
    }
    for (m = 0; m < 100; m++)
    {
        if (ret[m] > 9)
        {
            ret[m + 1] += ret[m] / 10;
            ret[m] %= 10;
        }
    }

}
void jia()
{
    int j;
    for (j = 0; j < 100; j++)
    {
        sum[j] += ret[j];
        if (sum[j] > 9)
        {
            sum[j + 1] += sum[j] / 10;
            sum[j] %= 10;
        }
    }
}
int main()
{
    int n;
    scanf("%d", &n);
    for (i = 1; i <= n; i++)
    {
        cheng();
        jia();

    }
    int k = 0;
    while (sum[k] != 0) k++;
    int j;
    for (j = 100; sum[j] == 0 && j > 0; j--);
    for (i = j; i >= 0; i--)
    {
        printf("%d", sum[i]);
    }
    return 0;
}

以上便是本蒟蒻的高精度模板，希望能帮到你，如果有dalao对我的代码有一些可以改进的地方欢迎指出。