RFLA: Gaussian Receptive Field based Label Assignment for Tiny Object Detection（ECCV2022）

hh
源代码

-

Abstract

微小目标的检测是阻碍目标检测技术发展的主要障碍之一。在微小目标检测任务中，一般目标检测器的性能有急剧下降的趋势。本文指出，对于微小目标，基于锚点的检测器中的盒先验和无锚检测器中的点先验都是次优的。我们的主要观察结果是，当前基于锚点或无锚点的标签分配范式将产生许多异常的微小的地面真值样本，导致检测器对微小物体的关注减少。为此，我们提出了一种基于高斯接受场的标签分配(RFLA)策略用于微小目标检测。具体来说，RFLA首先利用了特征接受野服从高斯分布的先验信息。然后，本文提出了一种新的感受野距离(RFD)来直接度量高斯感受野与地面真值之间的相似度，而不是使用IoU或中心采样策略来分配样本。考虑到基于IoU阈值和中心采样策略倾向于大对象，我们进一步设计了基于RFD的分层标签分配(HLA)模块，以实现对小目标的均衡学习。

在四个数据集上的大量实验证明了所提出方法的有效性。特别是，我们的方法在AI-TOD数据集上以4.0的AP点优于最先进的竞争对手

Introduction

微小物体的像素数量极其有限(AI-TOD中定义的小于16 × 16像素[49])，一直是计算机视觉界的一个难题。微小目标检测(Tiny Object Detection, TOD)是最具挑战性的任务之一，由于微小目标缺乏判别特征，一般的目标检测器通常无法在TOD任务上提供令人满意的结果[49,57]。考虑到微小物体的特殊性，提出了几种定制化的TOD基准(如AI-TOD[49]、TinyPerson[57]、AI-TOD-v2[51])，用于辅助驾驶、交通管理、海上救援等一系列下游任务。近年来，TOD逐渐成为一个独立于通用目标检测之外的热门但具有挑战性的方向[25,13]。

一般的对象检测器可以分为两类:基于锚点的和无锚点的。对于基于锚点的探测器，离散位置、尺度和纵横比的先验框是启发式预设的。然后，主要基于IoU构建标签分配策略(如Max IoU策略[39]、ATSS[58])，以寻找锚点与地面真值(gt)之间合适的匹配关系。无锚检测器将先验从方框变为点。通常将gt先验覆盖的点视为正样本(具有FCOS中的中心度[46])，从而节省了锚盒微调的工作量。

基于anchor的盒先验和无锚的点先验存在的问题

尽管上述两派在一般目标检测任务上表现出色，但它们在TOD任务上的表现通常会急剧下降[49,57]。在本文中，我们认为目前的先验盒和点及其相应的测量策略对于微小物体来说是次优的，这将进一步阻碍标签分配的过程。具体来说，我们以个体先验盒和点为实例，从分布的角度对其进行重新思考。

式中p(v|x,y)为先验信息的概率密度函数，(x,y)为图像上的位置，v为对应位置的权值，ε(·)为阶跃函数，当输入大于0时等于1，否则等于0。[(x1, y 1)，(x 2,y 2)]是先验信息区域，对于基于锚点的检测器，x 2−x 1 =宽度，y 2−y 1 =高度，而对于无锚点的检测器，x 2−x 1 = 1, y 2−y 1 = 1。

不同先验的原理图如图1第二行所示，现有先验信息及其对应的测量策略对于微小物体存在以下问题：

不同标签分配方案检测结果的比较。检测结果列在第一行。绿色、蓝色和红色方框表示真阳性(TP)、假阳性(FP)和假阴性(FN)预测。第二行是不同先验的原理图，其中绿色区域为gt，灰色、红色和黄色区域分别为盒、点和高斯先验。

首先，单个盒先验和点先验都有一个有限的先验域(其中p(v|x,y) > 0)，而现有的标签分配指标高度依赖于域的重叠。换句话说，当一个特定的gt与一个特定的先验没有重叠时，它们的位置关系不能通过IoU或中心来解决。对于微小物体，通常会出现gt盒与几乎所有锚盒没有重叠(即IoU = 0)或不包含锚点的情况[52]，导致微小物体缺乏阳性样本[52]。为此，通常采用启发式方法来保证微小物体的阳性样本[58,59]。然而，赋值者往往不能补偿基于零值IoU或中心的微小物体的阳性样本。因此，网络将减少对微小对象学习的关注。

其次，当前先验区域主要遵循均匀分布，对先验区域内的每个位置都平等对待(v =常数)。然而，先验信息基本上是用来辅助标签分配或特征点分配过程的[58]。在这个过程中，一个隐含的规则是为gt分配具有合适接受野的特征点[39,46]。如前人[29]的理论分析，将特征点的接受野重新映射到输入图像上时，有效的接受野实际上是高斯分布的。均匀分布的先验和高斯分布的接受野之间的差距将导致gt与分配给它的特征点的接受野之间的不匹配。

解决

为了解决上述问题，我们引入了一种新的基于高斯分布的先验，并构建了一个更有利于微小物体的基于高斯接受场的标签分配(RFLA)策略。具体来说，我们提出用一个新设计的感受野距离(RFD)来直接度量高斯感受野和gt区域之间的相似性。
利用高斯接受域作为先验信息可以很好地解决由框先验和点先验引起的问题。
一方面，高斯分布不是阶跃变化的。每个个体先验的域是整个图像，其中每个位置的权值从中心到外围逐渐衰减，其值大于0。因此，可以对整个图像上任意特征点与任意gt之间的位置关系进行建模，从而可以获得不同大小对象的平衡正样本。另一方面，高斯先验可以更好地拟合高斯有效感受野的性质，从而缓解感受野失配问题，特别是对于微小物体。

此外，由于IoU和RFD不在同一维度，直接将新度量应用于现有的基于阈值的标签分配结构是不合理的。在此基础上，我们进一步设计了一个分层标签分配器(HLA)，逐步减少了离群样本，并获得了对微小物体的充分训练。

Contributions

(1)实验表明，目前基于锚点和无锚点的检测器在微小目标标签分配中存在尺度-样本不平衡问题。
(2)为了解决上述问题，我们引入了一种简单而有效的基于可接受域的标签分配(RFLA)策略。RFLA很容易取代主流检测器中的标准盒和基于点的标签分配策略，提高了它们在TOD上的性能。
(3)在4个数据集上的大量实验验证了本文方法的性能优越性。引入的方法在具有挑战性的AI-TOD数据集上显著优于最先进的竞争对手，而在推理阶段没有额外的成本。

Related Work

Object Detection

主流的目标检测方法包括基于锚点的检测器和无锚点的检测器。经典的基于锚点的检测器包括Faster R-CNN[39]、Cascade R-CNN[4]、RetinaNet[24]、YOLO系列[37,38,3]等。人们普遍认为，基于锚点的范式的一个基本缺陷是它需要根据具体任务进行调整[46]。此外，基于IoU的标签分配策略[39]也引入了额外的超参数，对检测性能产生了重大影响。

无锚点检测器摆脱锚盒的约束，寻求直接从中心点预测目标，如FCOS[46]和FoveaBox[19]，或寻求从关键点预测目标，如CornerNet[20]、Grid R-CNN[28]和RepPoints[55]。最近发表的无锚点检测器主要遵循端到端范式，它们只是预设一组没有形状或位置先验信息的盒子，然后直接对最终预测进行推理，如DETR[5]、Deformable DETR[64]和Sparse R-CNN[44]。尽管端到端范式在通用对象检测任务上取得了成功，但它们在TOD任务上的性能需要进一步研究。

与基于盒和点先验的检测器不同，我们引入了另一种基于接受野的先验信息。结合高斯感受野及其自定义标签分配策略，可以显著缓解现有先验和测量方法对微小物体的不平衡问题。

Tiny Object Detection

现有的大多数微小目标检测方法大致可以分为以下四类:数据增强、多尺度学习、针对微小目标的定制训练策略和特征增强策略

Data augmentation（2023那篇综述里给了一堆方法）

一个简单而有效的方法是收集更多的微小对象数据。另一种方法是使用简单的数据增强，包括旋转、图像翻转和上采样。Krisantal等人[18]试图通过对包含微小物体的图像进行过采样并复制粘贴来提高TOD性能。

Multi-scale learning

多分辨率图像金字塔是多尺度学习的一种基本方法。为了降低计算成本，一些研究[27,23,61]提出构建特征级金字塔。此后，许多方法试图进一步改进FPN，如PANet[26]、BiFPN[45]、Recursive- FPN[35]等。此外，TridentNet[22]构建了具有不同接受野的多分支检测头来生成特定尺度的特征图。多尺度学习策略通常通过额外的计算来提高TOD性能.

Customized training strategy for tiny objects

目标检测器通常不能同时对微小目标和大型目标获得满意的性能。受此启发，SNIP[42]和SNIPER[43]被设计为在一定尺度范围内选择性地训练对象。此外，Kim等人[17]引入了尺度感知网络(SAN)，并将不同空间的特征映射到尺度不变的子空间上，使检测器对尺度变化具有更强的鲁棒性。

Feature enhancement strategy

一些研究提出用超解或GAN来增强小物体的特征表示。PGAN[21]首次尝试将GAN应用于小目标检测。此外，Bai等人[1]提出了一种MT-GAN，该gan训练图像级超分辨率模型来增强小RoI特征。提出了特征级超分辨率[32]来提高基于提议的检测器的小目标检测性能。此外，还有其他一些基于超解的方法，包括[8,2,36]。

大多数专用于TOD的方法都会带来额外的注释或计算成本。相比之下，我们提出的方法试图从标签分配的角度推进TOD，我们提出的策略在推理阶段不会带来任何额外的成本。

Label Assignment in Object Detection

正如ATSS[58]所揭示的，无锚点检测器和基于锚点检测器的本质区别在于定义训练样本的方式。正负(pos/ negative)训练样本的选择会显著影响检测器的性能。近年来，为了在通用目标检测任务中更好地分配标签，人们提出了许多工作。FreeAnchor[60]根据检测自定义的可能性决定正锚。PAA[16]提出使用GMM对锚点分布进行建模，并基于GMM的中心划分pos/neg样本。OTA[14]将标签分配过程建模为最优运输问题，寻求解决最优分配策略。ATSS[58]根据正负样本的统计特征自适应调整正负样本。AutoAssign[62]和IQDet[30]根据预测的借据和置信度重新加权和采样高质量区域。与上述一般目标检测策略不同，本文重点研究TOD的先验信息设计及其相应的标签分配策略。

Method

Receptive Field Modelling

主流目标检测器遵循的一个基本原则是分而治之，即在FPN的不同层上检测不同尺度的目标[7,23]。具体来说，基于锚点的检测器在FPN的不同层上平铺不同尺度的先验盒来辅助标签分配，从而在FPN的不同层上检测到不同尺度的物体。对于无锚探测器，他们将不同尺度范围内的物体(例如p3的[0,64])分组到不同的FPN级别进行检测。尽管标签分配策略各不相同，但基于锚点和无锚点的检测器的共同点是为不同尺度的对象分配适当的接受场的特征点[39,46]。因此，在不设计启发式锚盒预设或尺度分组的情况下，感受野可以直接作为标签分配的可靠先验。

本文提出直接测量有效感受野(ERF)与gt区域之间的匹配程度来进行标签分配，从而去除导致TOD恶化的盒子或点。前人的研究指出，ERF可以从理论上推导为高斯分布[29]。在这项工作中，我们遵循这一范式，并寻求将每个特征点的ERF建模为高斯分布，我们首先推导出标准卷积神经网络[15]上第n层的理论接受场(Theoretical Receptive Field, TRF)，公式为tr n:

tr n表示第n卷积层各点的TRF, k n和s n表示第n层卷积操作的核大小和步幅。

如[29]研究，ERF和TRF具有相同的中心点，但每个特征点的ERF只占整个TRF的一部分。因此，我们使用每个特征点(x n,y n)的位置作为标准二维高斯分布的平均向量。由于很难得到精确的ERF，我们用TRF半径的一半来近似ERF半径。对于标准的类平方卷积核，ern的平方作为二维高斯分布的协方差。综上所述，我们将ERF的范围建模为二维高斯分布Ne(µe，Σ e)

Receptive Field Distance

获得高斯ERF后，接下来的关键步骤是测量特征点的ERF与某个gt之间的匹配程度。如引言所述，变阶均匀分布不利于微小物体，还需要将gt建模为另一种分布。
观察到物体主体聚集在边界框的中心[50,48]，我们也将gt框(x g,y g,w g,h g)建模为标准的二维高斯分布N g(µg，Σ g)，其中每个标注框的中心点作为高斯均值向量，半边长平方作为协方差矩阵，即:
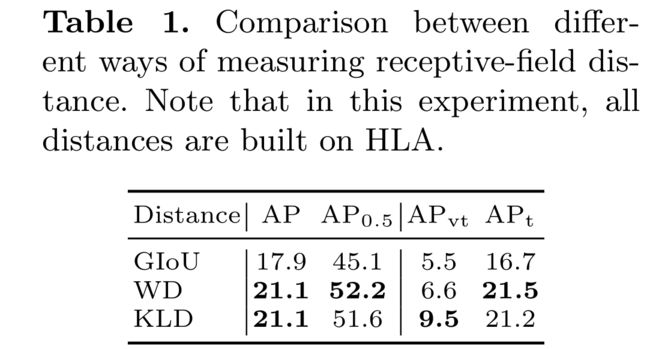
本文研究了三种典型的高斯分布之间的距离作为接收野距离候选者(RFDC)。这些距离测量包括Wasserstein距离[34,53]、K-L散度[11,54]和J-S散度[12]。高斯分布之间的J-S散度没有闭合解[12,31]，在逼近其解时会引入巨大的计算量，因此不使用J-S散度。在这里，我们将首先分析它们在任务中的封闭形式解决方案，然后讨论它们在TOD任务中的优缺点。
瓦瑟斯坦的距离：Wasserstein距离来自最优运输理论[34]。假设高斯ERF N e = N e(µe，Σ e)，高斯gt N g = N g(µg，Σ g)，则第2 Wasserstein距离可简化为式5[53]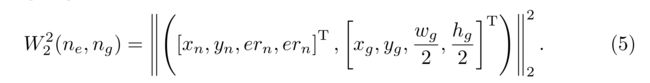
Wasserstein距离的主要优点是它可以测量两个不重叠的分布[34]。通常情况下，gt盒子与大多数先前的盒子和点没有重叠，分配者无法将这些候选的优先级排序到某个gt。因此，可以说Wasserstein距离的特性有利于TOD，它可以一致地反映所有特征点与某个gt盒的匹配程度，使得分配者可以根据合理的优先级对微小物体补偿更多的阳性样本。然而，Wasserstein距离不是尺度不变的，当数据集包含大规模方差的对象时，它可能是次优的[54]。

Kullback-Leibler divergence：Kullback-Leibler散度(KLD)是衡量一个概率分布与另一个概率分布差异程度的经典统计距离。两个高斯分布之间的KLD也有闭形式解，ERF n e与gt区域n g之间的KLD如下:
可以进一步简化为:

如文献[54]所示，KLD在两个二维高斯分布之间具有尺度不变性，而尺度不变性对于检测至关重要[56]。而KLD的主要缺点是，当两个分布的重叠可以忽略不计时，它不能一致地反映两个分布之间的距离。因此，本文选择ERF与gt之间的KLD作为另一个RFDC。

综上所述，我们研究了三种经典的概率分布测量方法，选择Wasserstein距离和KLD作为RFDC。然后，对RFDC进行非线性变换，得到归一化范围在(0,1)之间的RFD:

Hierarchical Label Assignment

一些基于锚点的检测器根据IoU设置阈值来确定pos/ neg样本[39,24,4]，而无锚点检测器主要通过点先验和gt区域之间的空间位置来划分pos/ neg样本。由于在基于阈值和基于gt区域的策略中，微小对象通常都不受欢迎，我们建议通过分数排序分层地为微小对象分配标签。为了保证任意特征点与任意gt之间的位置关系能够求解，在该RFD的基础上构建了HLA (Hierarchical Label Assignment)策略。在分配之前，根据上述方法计算特征点与gt之间的RFD评分矩阵。
在第一阶段，我们对每个特征点按一定的gt对其RFD评分进行排序。然后，对具有一定gt的RFD评分前k的特征点分配正标签。最后，我们得到分配结果r 1和已分配特征对应的掩码m，其中m为二值(0/1)。
在第二阶段，为了提高整体召回率和缓解异常值，我们通过乘以阶段因子β来轻微衰减有效半径er n，然后重复上述排序策略，并为每个gt补充一个阳性样本，得到分配结果r 2。我们根据以下规则得到最终赋值结果r:
对于已经分配了足够的样品的gt，采取mask操作m，以避免引入过多的低质量样品，并不是说被遮挡的样本将被分配到较小的gt。将RFD与HLA策略相结合，我们可以得到TOD的完整的基于感受野的标签分配(RFLA)策略。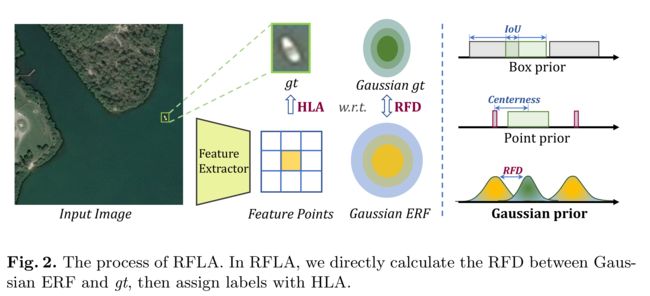

Application to Detectors

所提出的RFLA策略可以很容易地应用于基于锚点和无锚点的框架。在不失一般性的前提下，我们以经典的Faster R-CNN[39]和FCOS[46]为例。具体来说，对于Faster R-CNN, RFLA可以代替标准的锚点平铺和MaxIoU锚点分配过程。对于FCOS，由于小盒子只覆盖一个非常有限的区域，通常比大物体包含的特征点要少得多，因此我们消除了小盒子内限制特征点的约束。然后，很容易用RFLA代替基于点的分配来实现平衡学习。注意，为避免梯度爆炸，我们将中心度[46]损失修改为如下公式:

l∗，t∗，r∗，b∗是在FCOS中定义的回归目标，ε(·)是与式1相同的阶跃函数，c是为避免回归目标中心点在gt盒外时梯度消失问题而设为0.01的因子

Experiment

Dataset

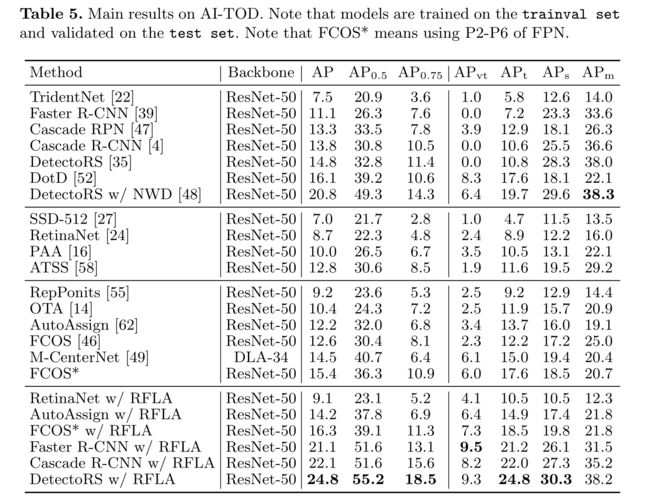
实验在四个数据集上进行。主要实验是在具有挑战性的AI-TOD[49]数据集上进行的，该数据集的平均绝对对象大小最小，为12.8像素，包含28,036张图像。此外，我们在TinyPerson[57]、VisDrone2019[10]和DOTA- v2.0[9]上测试了所提出的方法。请注意，所选数据集都包含大量的微小对象(小于16 × 16像素)。

Ablation Study

Effectiveness of different RFD

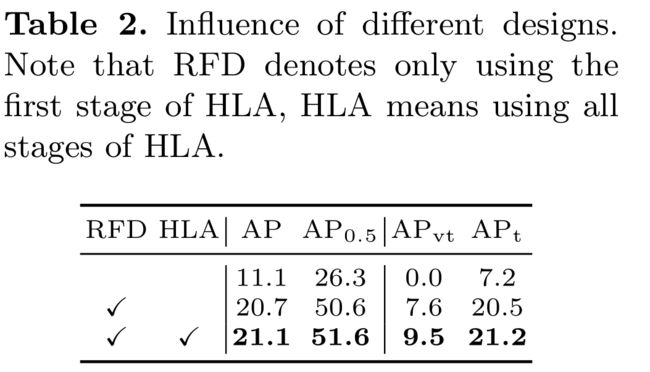
Effectiveness of individual component

RFD只表示使用第一阶段的HLA, HLA意味着使用所有阶段的HLA

Performance of different decay factor β

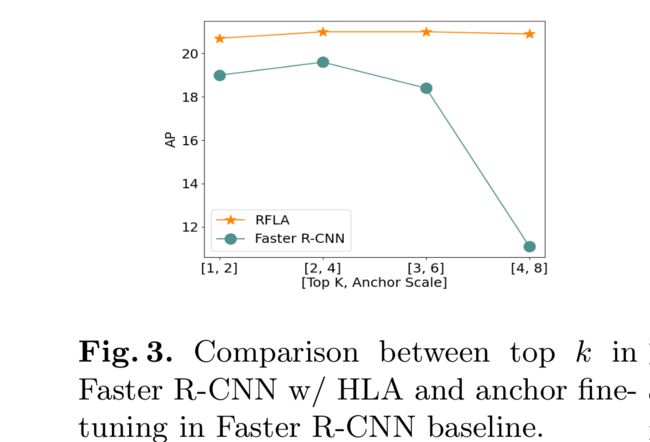
Performance of different k

Gaussian anchor and receptive anchor

Main result

Analysis

图4中的观测结果表明，现有检测器存在严重的尺度-样本不平衡问题。对于基于锚点的检测器，在小尺度和盒尺度之间的间隔对象成为异常值，无锚探测器在一定程度上缓解了这个问题。然而，微小物体仍然是异常值，因为微小物体覆盖的区域非常有限。gt内部的先验点的数量比大型对象的要少得多。尺度-样本不平衡问题会误导网络走向不平衡优化，即对离群样本的关注较少。相比之下，在不同尺度范围内分配给gt的阳性样本数量在RFLA上是高度一致的，实现了对微小物体的平衡优化。

Conclusion

在本文中，我们指出盒先验和点先验对TOD不适用，在分配标签时导致尺度-样本不平衡问题。为此，我们引入了一种新的高斯接收野先验。然后，我们进一步设计了一个新的感受野距离(RFD)来衡量ERF和gt之间的相似性，以克服IoU和中心采用策略对TOD的不足？。RFD与HLA策略协同工作，实现对微小对象的均衡学习。在4个数据集上的实验证明了该方法的优越性和鲁棒性。