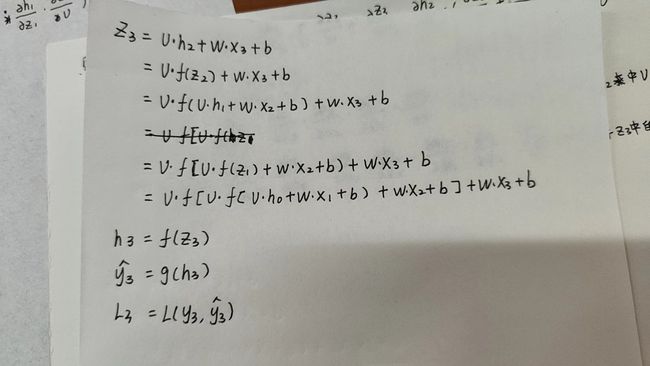【23-24 秋学期】NNDL 作业10 BPTT
习题6-1P 推导RNN反向传播算法BPTT.
已知,z1---f激活函数--h1,h1--g激活函数--
,y1是真实值。
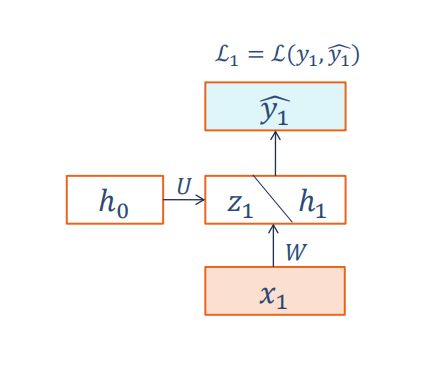
(1)T=1时【图截自老师ppt】:
由上图可知:
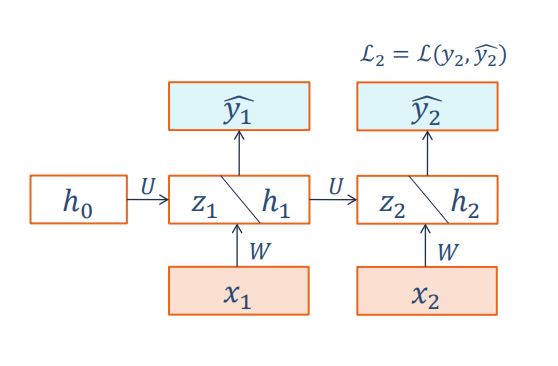
(2)T=2时:
可得:
(3)T=3时:
可得:
因为:
可知:
与老师的相符:
习题6-2 推导公式(6.40)和公式(6.41)中的梯度.
即推导以下公式:
(1)W:
(2)b:
习题6-3 当使用公式(6.50)作为循环神经网络的状态更新公式时, 分析其可能存在梯度爆炸的原因并给出解决方法.
(1)原因
然后我自己理解如下:
而这个误差项又等于:【手误:W>4是梯度爆炸,W<4时梯度消失】
(2)梯度爆炸的解决方法:
进一步的改进:
习题6-2P 设计简单RNN模型,分别用Numpy、Pytorch实现反向传播算子,并代入数值测试.
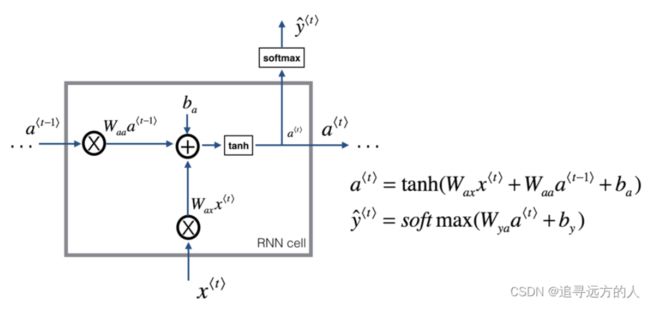
RNN单元如下:【图来自L5W1作业1 手把手实现循环神经网络-CSDN博客】
手写实现 RNN一个单元的前向计算和反向传播,得到:
import numpy as np
import torch.nn
# hidden---->output
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
# 前向传播
# xt:输入,a_pred:上一个隐藏层
def rnn_cell_forward(xt, a_prev, parameters):
# 参数是上图中的参数
Wax = parameters["Wax"] # 输入向量x的权重
Waa = parameters["Waa"] # 状态权重
Wya = parameters["Wya"] # 激活后得到at的权重
ba = parameters["ba"] #偏置
by = parameters["by"] #激活后得到at在进行计算的偏置
# 新的隐藏层【也就是延时器+输入层再激活】
a_next = np.tanh(np.dot(Wax, xt) + np.dot(Waa, a_prev) + ba)
#输出
yt_pred=softmax(np.dot(Wya,a_next)+by)
cache=(a_next,a_prev,xt,parameters)
return a_next,yt_pred,cache
#反向传播
def rnn_cell_backward(da_next,cache):
(a_next, a_prev, xt, parameters) = cache
#参数
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
#求激活函数tanh的导数
dtanh = (1 - a_next * a_next) * da_next
#求解x的导
dxt = np.dot(Wax.T, dtanh)
#求解输入权重的导
dWax = np.dot(dtanh, xt.T)
da_prev = np.dot(Waa.T, dtanh)
#状态权重导数
dWaa = np.dot(dtanh, a_prev.T)
#偏置
dba = np.sum(dtanh, keepdims=True, axis=-1)
gradients = {"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba}
return gradients
np.random.seed(1)
xt = np.random.randn(3, 10)
a_prev = np.random.randn(5, 10)
Wax = np.random.randn(5, 3)
Waa = np.random.randn(5, 5)
Wya = np.random.randn(2, 5)
ba = np.random.randn(5, 1)
by = np.random.randn(2, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
#先进行前向计算得到cache
a_next, yt, cache = rnn_cell_forward(xt, a_prev, parameters)
da_next = np.random.randn(5, 10)
#调用反向传播函数求解梯度
gradients = rnn_cell_backward(da_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)
手写实现RNN模型前向计算
#实现RNN模型的前向计算
def rnn_forward(x, a0, parameters):
caches = []
#n_x:inputs维度,m:样本数量,T_x:时间步长
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wya"].shape
#对隐向量初始化
a = np.zeros((n_a, m, T_x))
#输出初始化
y_pred = np.zeros((n_y, m, T_x))
a_next = a0
#循环调用rnn_cell_forward函数计算隐藏层和输出层
for t in range(T_x):
a_next, yt_pred, cache = rnn_cell_forward(x[:, :, t], a_next, parameters)
a[:, :, t] = a_next
y_pred[:, :, t] = yt_pred
caches.append(cache)
caches = (caches, x)
return a, y_pred, caches
#实例化
np.random.seed(1)
x = np.random.randn(3, 10, 4)
a0 = np.random.randn(5, 10)
Waa = np.random.randn(5, 5)
Wax = np.random.randn(5, 3)
Wya = np.random.randn(2, 5)
ba = np.random.randn(5, 1)
by = np.random.randn(2, 1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}
a, y_pred, caches = rnn_forward(x, a0, parameters)
print("a[4][1] = ", a[4][1])
print("a.shape = ", a.shape)
print("y_pred[1][3] =", y_pred[1][3])
print("y_pred.shape = ", y_pred.shape)
print("caches[1][1][3] =", caches[1][1][3])
print("len(caches) = ", len(caches))#反向计算
class RNNCell:
def __init__(self, weight_ih, weight_hh,
bias_ih, bias_hh):
#初始化
self.weight_ih = weight_ih#input-->hidden
self.weight_hh = weight_hh#hidden-->hidden
self.bias_ih = bias_ih#input-->hidden
self.bias_hh = bias_hh#hidden--->hidden
self.x_stack = []#保存每个时间的输入
self.dx_list = []#保存每个时间的输入梯度
# 保存每个事件的权重梯度
self.dw_ih_stack = []#input-->hidden
self.dw_hh_stack = []#hidden-->hidden
# 保存每个事件的偏置梯度
self.db_ih_stack = []
self.db_hh_stack = []
#hidden
self.prev_hidden_stack = []
#the next hidden
self.next_hidden_stack = []
self.prev_dh = None
#调用方法:根据x和上一个hidden得到next hidden
def __call__(self, x, prev_hidden):
self.x_stack.append(x)
next_h = np.tanh(
np.dot(x, self.weight_ih.T)
+ np.dot(prev_hidden, self.weight_hh.T)
+ self.bias_ih + self.bias_hh)
self.prev_hidden_stack.append(prev_hidden)
self.next_hidden_stack.append(next_h)
self.prev_dh = np.zeros(next_h.shape)
return next_h
#反向传播
def backward(self, dh):
x = self.x_stack.pop()
prev_hidden = self.prev_hidden_stack.pop()
next_hidden = self.next_hidden_stack.pop()
#计算梯度【类似前边写过的反向传播】
d_tanh = (dh + self.prev_dh) * (1 - next_hidden ** 2)
self.prev_dh = np.dot(d_tanh, self.weight_hh)
dx = np.dot(d_tanh, self.weight_ih)
self.dx_list.insert(0, dx)
dw_ih = np.dot(d_tanh.T, x)
self.dw_ih_stack.append(dw_ih)
dw_hh = np.dot(d_tanh.T, prev_hidden)
self.dw_hh_stack.append(dw_hh)
self.db_ih_stack.append(d_tanh)
self.db_hh_stack.append(d_tanh)
return self.dx_list
if __name__ == '__main__':
np.random.seed(123)
torch.random.manual_seed(123)
np.set_printoptions(precision=6, suppress=True)
rnn_PyTorch = torch.nn.RNN(4, 5).double()
rnn_numpy = RNNCell(rnn_PyTorch.all_weights[0][0].data.numpy(),
rnn_PyTorch.all_weights[0][1].data.numpy(),
rnn_PyTorch.all_weights[0][2].data.numpy(),
rnn_PyTorch.all_weights[0][3].data.numpy())
nums = 3
x3_numpy = np.random.random((nums, 3, 4))
x3_tensor = torch.tensor(x3_numpy, requires_grad=True)
h3_numpy = np.random.random((1, 3, 5))
h3_tensor = torch.tensor(h3_numpy, requires_grad=True)
dh_numpy = np.random.random((nums, 3, 5))
dh_tensor = torch.tensor(dh_numpy, requires_grad=True)
h3_tensor = rnn_PyTorch(x3_tensor, h3_tensor)
h_numpy_list = []
h_numpy = h3_numpy[0]
for i in range(nums):
h_numpy = rnn_numpy(x3_numpy[i], h_numpy)
h_numpy_list.append(h_numpy)
h3_tensor[0].backward(dh_tensor)
for i in reversed(range(nums)):
rnn_numpy.backward(dh_numpy[i])
#对比pytorch和numpy
print("numpy_hidden :\n", np.array(h_numpy_list))
print("tensor_hidden :\n", h3_tensor[0].data.numpy())
print("------")
print("dx_numpy :\n", np.array(rnn_numpy.dx_list))
print("dx_tensor :\n", x3_tensor.grad.data.numpy())
print("------")
print("dw_ih_numpy :\n",
np.sum(rnn_numpy.dw_ih_stack, axis=0))
print("dw_ih_tensor :\n",
rnn_PyTorch.all_weights[0][0].grad.data.numpy())
print("------")
print("dw_hh_numpy :\n",
np.sum(rnn_numpy.dw_hh_stack, axis=0))
print("dw_hh_tensor :\n",
rnn_PyTorch.all_weights[0][1].grad.data.numpy())
print("------")
print("db_ih_numpy :\n",
np.sum(rnn_numpy.db_ih_stack, axis=(0, 1)))
print("db_ih_tensor :\n",
rnn_PyTorch.all_weights[0][2].grad.data.numpy())
print("------")
print("db_hh_numpy :\n",
np.sum(rnn_numpy.db_hh_stack, axis=(0, 1)))
print("db_hh_tensor :\n",
rnn_PyTorch.all_weights[0][3].grad.data.numpy())得到输出为:
numpy_hidden :
[[[ 0.4686 -0.298203 0.741399 -0.446474 0.019391]
[ 0.365172 -0.361254 0.426838 -0.448951 0.331553]
[ 0.589187 -0.188248 0.684941 -0.45859 0.190099]]
[[ 0.146213 -0.306517 0.297109 0.370957 -0.040084]
[-0.009201 -0.365735 0.333659 0.486789 0.061897]
[ 0.030064 -0.282985 0.42643 0.025871 0.026388]]
[[ 0.225432 -0.015057 0.116555 0.080901 0.260097]
[ 0.368327 0.258664 0.357446 0.177961 0.55928 ]
[ 0.103317 -0.029123 0.182535 0.216085 0.264766]]]
tensor_hidden :
[[[ 0.4686 -0.298203 0.741399 -0.446474 0.019391]
[ 0.365172 -0.361254 0.426838 -0.448951 0.331553]
[ 0.589187 -0.188248 0.684941 -0.45859 0.190099]]
[[ 0.146213 -0.306517 0.297109 0.370957 -0.040084]
[-0.009201 -0.365735 0.333659 0.486789 0.061897]
[ 0.030064 -0.282985 0.42643 0.025871 0.026388]]
[[ 0.225432 -0.015057 0.116555 0.080901 0.260097]
[ 0.368327 0.258664 0.357446 0.177961 0.55928 ]
[ 0.103317 -0.029123 0.182535 0.216085 0.264766]]]
------
dx_numpy :
[[[-0.643965 0.215931 -0.476378 0.072387]
[-1.221727 0.221325 -0.757251 0.092991]
[-0.59872 -0.065826 -0.390795 0.037424]]
[[-0.537631 -0.303022 -0.364839 0.214627]
[-0.815198 0.392338 -0.564135 0.217464]
[-0.931365 -0.254144 -0.561227 0.164795]]
[[-1.055966 0.249554 -0.623127 0.009784]
[-0.45858 0.108994 -0.240168 0.117779]
[-0.957469 0.315386 -0.616814 0.205634]]]
dx_tensor :
[[[-0.643965 0.215931 -0.476378 0.072387]
[-1.221727 0.221325 -0.757251 0.092991]
[-0.59872 -0.065826 -0.390795 0.037424]]
[[-0.537631 -0.303022 -0.364839 0.214627]
[-0.815198 0.392338 -0.564135 0.217464]
[-0.931365 -0.254144 -0.561227 0.164795]]
[[-1.055966 0.249554 -0.623127 0.009784]
[-0.45858 0.108994 -0.240168 0.117779]
[-0.957469 0.315386 -0.616814 0.205634]]]
------
dw_ih_numpy :
[[3.918335 2.958509 3.725173 4.157478]
[1.261197 0.812825 1.10621 0.97753 ]
[2.216469 1.718251 2.366936 2.324907]
[3.85458 3.052212 3.643157 3.845696]
[1.806807 1.50062 1.615917 1.521762]]
dw_ih_tensor :
[[3.918335 2.958509 3.725173 4.157478]
[1.261197 0.812825 1.10621 0.97753 ]
[2.216469 1.718251 2.366936 2.324907]
[3.85458 3.052212 3.643157 3.845696]
[1.806807 1.50062 1.615917 1.521762]]
------
dw_hh_numpy :
[[ 2.450078 0.243735 4.269672 0.577224 1.46911 ]
[ 0.421015 0.372353 0.994656 0.962406 0.518992]
[ 1.079054 0.042843 2.12169 0.863083 0.757618]
[ 2.225794 0.188735 3.682347 0.934932 0.955984]
[ 0.660546 -0.321076 1.554888 0.833449 0.605201]]
dw_hh_tensor :
[[ 2.450078 0.243735 4.269672 0.577224 1.46911 ]
[ 0.421015 0.372353 0.994656 0.962406 0.518992]
[ 1.079054 0.042843 2.12169 0.863083 0.757618]
[ 2.225794 0.188735 3.682347 0.934932 0.955984]
[ 0.660546 -0.321076 1.554888 0.833449 0.605201]]
------
db_ih_numpy :
[7.568411 2.175445 4.335336 6.820628 3.51003 ]
db_ih_tensor :
[7.568411 2.175445 4.335336 6.820628 3.51003 ]
------
db_hh_numpy :
[7.568411 2.175445 4.335336 6.820628 3.51003 ]
db_hh_tensor :
[7.568411 2.175445 4.335336 6.820628 3.51003 ]总结:
及时复习很重要!在前边的公式推导以及第三问为什么会梯度爆炸,我发现我的脑子是空的,然后我个人强推哔哩哔哩上的一个课,时间不是很长,但是听了以后再加上我自己消化老师的ppt,就成功推导出来了,感觉推导困难的小伙伴可以去看!指路:循环神经网络讲解|随时间反向传播推导(BPTT)|RNN梯度爆炸和梯度消失的原因|LSTM及GRU(解决RNN中的梯度爆炸和梯度消失)-跟李沐老师动手学深度学习_哔哩哔哩_bilibili
这个博主讲的关于为什么会梯度爆炸、梯度消失我也觉得挺好的,然后我前边的思路是按照他讲的写的。
1.有关RNN反向传播算法
前馈神经网络反向推导:NNDL:作业四:分别使用numpy和pytorch实现FNN例题-CSDN博客 卷积神经网络反向推导:【23-24 秋学期】NNDL 作业8 卷积 导数 反向传播-CSDN博客
参考上边的反向推导,可以发现在推导过程中RNN与前边的前馈神经网络、卷积神经网络不同地方就是权重共享,多了的延迟器也类似前馈的偏置。损失函数是全过程的损失函数之和,然后关于损失对U\W\b的求导过程可以看本文的前边。
2.有关梯度爆炸
梯度爆炸可以从前边的推导中看到:是因为再计算误差项时如果隐藏层过多或者误差项过大就会导致最后会出现梯度爆炸情况,解决梯度爆炸就需要引入门控装置。
3.设计RNN模型
这一块我是参考的舍友【23-24 秋学期】NNDL 作业10 BPTT-CSDN博客
然后我个人的理解,第一部分的代码,就是照着图写了一遍前向传播反向传播的流程,是一个小的单元部分,第二部分的代码就是实现RNN这个大模型,可以加入时间步长;第三部分就是对RNN一个小单元分别使用手写numpy和pytorch比较反向传播得到的梯度值。
作业参考:
HBU_David_Database,DeepLearning,AI-CSDN博客