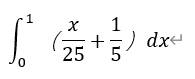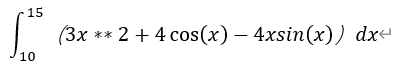Python-蒙特卡罗应用
第1关:蒙特卡洛方法求定积分一
任务描述
本关任务:用蒙特卡罗方法求函数f(x)=(x/25+1/5),在区间[a,b]中定积分。假设a=0,b=1,即求
要求将函数f(x)定义为匿名函数,求出的积分保留5位小数,a,b的值可以自定义。
import numpy as np
#将积分函数f定义成匿名函数
# # # # # # # # # # #begin # # # # # # # # # # # #
f = lambda x: x / 25 + 1 / 5
# # # # # # # # # # #end # # # # # # # # # # # # # #
#在一行输入积分区间【 a, b】 和实验点数n, 用空格分隔
# # # # # # # # # # # # # # # # # #begin # # # # # # # # # # # # # # #
m = input()
m = list(map(int, m.split()))
a = int(m[0])
b = int(m[1])
n = int(m[2])
# # # # # # # # # # # # # # # # # # #end # # # # # # # # # # # # # # # #
#矩形区域为:[a, b, fmin, fmax], 矩形面积 = (b - a) * (fmax - fim)
fmin = 0
fmax = f(b)
np.random.seed(0)
#利用均匀分布产生n个在【 a, b】 中的随机数x
#利用均匀分布产生n个在【 fmin, fmax】 中的随机数y
# # # # # # # # # # # # # # # # #begin # # # # # # # # # # # # # # # # # #
x = np.random.uniform(a, b, n)
y = np.random.uniform(fmin, fmax, n)
# # # # # # # # # # # # # # # # # #end # # # # # # # # # # # # # # # # # #
#统计落在y < f(x) 内的点数
p = y[(y > 0) & (y < f(x))].size
#积分面积为y < f(x) 内点数除以总实验点数再乘以矩形面积
# # # # # # # # # # # # # #begin # # # # # # # # # # # # # # # #
jf = p / n * (b - a) * (fmax - fmin)
# # # # # # # # # # # # # # # # #end # # # # # # # # # # # # # # #
print("%.5f" % jf)第2关:蒙特卡罗方法求定积分二
任务描述
本关任务:用蒙特卡罗方法求下面定积分。
要求将积分函数
定义成一个自定义函数,将第一关求积分也定义成一个自定义函数。求得的结果保留4位小数。
import numpy as np
#定义积分函数f(x)
##################begin####################
f = lambda x:3*x**2+4*np.cos(x)-4*x*np.sin(x)
##################end#######################
#定义求积分值的函数
def jifen(f, a, b, n, fmin,fmax):
#f表示积分函数
#a,b表示积分区间
#n表示总实验点数
#fmin,fmax矩形区域纵向最小和最大值
##################begin#################
x = np.random.uniform(a, b, n)
y = np.random.uniform(fmin, fmax, n)
cnt = y[ (y>0) & (y < f(x))].size #横轴上方部分
cnt-= y[ (y<0) & (y > f(x))].size #横轴下方积分为负数
area = cnt/n*(b-a)*(fmax-fmin)
return area
###################end###################
np.random.seed(17)
n=int(input())
fmin=0
fmax=f(15)
z=jifen(f, 10,15, n, fmin,fmax)
print("{0:.4f}".format(z))第3关:蒙特卡洛方法求圆周率
任务描述
本关任务:考虑一个圆的方程x2+y2=1,用蒙特卡洛方法求圆周率,得到的结果保留4位小数。
'''求x**2+y**2=1在【-1,1】中的积分
即求y=np.sqrt(1-x**2)在【-1,1】中积分
即求上半圆的面积,np.pi*1**2/2
利用该积分得到的面积可以求出圆周率'''
import numpy as np
#定义积分函数f(x)
#########begin###############
f = lambda x:np.sqrt(1-x**2)
###########end################
def jifen(f, a, b, n, fmin,fmax):
#f表示积分函数
#a,b表示积分区间,矩形区域横向值
#n表示总实验点数
#fmin,fmax矩形区域纵向最小和最大值
#利用均匀分布产生n个在【a,b】中的随机数x
#利用均匀分布产生n个在【fmin,fmax】中的随机数y
############begin#############
x = np.random.uniform(a, b, n)
y = np.random.uniform(fmin, fmax, n)
cnt = y[ (y>0) & (y < f(x))].size #横轴上方部分
cnt-= y[ (y<0) & (y > f(x))].size #横轴下方积分为负数
jf = cnt/n*(b-a)*(fmax-fmin)
###########end##################
return jf
np.random.seed(11)
n=int(input())
#调用自定函数求f(x)在【0,1】中积分
#############begin#############
z=jifen(f, 0, 1, n,0,1)
#############end###############
#调用自定函数求f(x)在【-1,0】中积分
z1=jifen(f, -1, 0, n, 0,1)
w=z+z1 #上半圆的面积,半径为1,即圆周率的一半
print("{0:.4f}".format(w*2))