第三十二周：文献阅读+RNN+SVM

目录

摘要

Abstract

文献阅读：深度学习递归神经网络预测水体浊度的鲁棒性研究

存在的问题

提出的方法

研究使用的方法

神经网络（NN）

递归神经网络（RNN1）

递归神经网络（RNN2）

 研究分析的步骤

研究实验

数据集

评估指标

实验目的

实验内容

实验结果

研究结论

SVM-解决线性不可分问题

思路一：引入松弛变量和惩罚因子

思路二：低维映射到高维

如何划分非线性数据

 核函数

---

摘要

本周阅读的文献是关于递归神经网络预测水体浊度的鲁棒性研究，该文献研究的重点是使用鲁棒深度学习模型来分析时间序列数据，以预测库区浊度的水质。本文的新颖之处在于使用了两个神经网络系统，一个人工神经网络系统用于常规无雨时间，RNN2系统用于子程序即当考虑下雨时间。利用光学波段构建回归函数监测水体浊度，然后利用递归神经网络(RNN2)模型对时间序列浊度数据进行分析。根据使用数据、预测水平和训练时间的准确性来比较所选模型的准确性。在上周学习了SVM解决线性可分问题，然而SVM也可以用来解决线性不可分问题，通过引入松弛变量和惩罚因子或者利用核函数将低维映射到高维两种思路，可以将线性不可分问题转化为线性可分问题，从而得出划分的超平面。

Abstract

The literature read this week is about the robustness research of recursive neural networks for predicting water turbidity. The focus of this literature research is to use robust deep learning models to analyze time series data to predict the water quality of reservoir turbidity. The novelty of this article lies in the use of two neural network systems, one artificial neural network system for conventional no rain time, and the RNN2 system for subroutines when considering rain time. Construct a regression function using optical bands to monitor water turbidity, and then use a recurrent neural network (RNN2) model to analyze time series turbidity data. Compare the accuracy of the selected model based on usage data, prediction level, and training time. Last week learned how to solve linearly separable problems using SVM. However, SVM can also use to solve linearly separable problems. By introducing relaxation variables and penalty factors, or using kernel functions to map low dimensions to high dimensions, we can transform linearly separable problems into linearly separable problems and obtain the hyperplane for partitioning.

文献阅读：深度学习递归神经网络预测水体浊度的鲁棒性研究

title：The Robust Study of Deep Learning Recursive Neural Network for Predicting of Turbidity of Water

Shiuan Wan1author：Shiuan Wan1; Mei-Ling Yeh2; Hong-Lin Ma3; Tein-Yin Chou4

time：2022

D O I：10.3390/w14050761

存在的问题

过去监测环境的研究可以根据所使用的两种系统进行划分：监测系统或决策支持系统。这些系统大多是在考虑水库周边水体和土地利用等因素的基础上建立的，而水质的变化是难以预测的，它也可能受到气候因子的影响，水的浑浊度是一个主要因素，在水系统的下游由水处理厂净化。而大多数浑浊问题是由暴雨后的滑坡或流域非法土地使用引起的，因此需要检测地理环境变化。如果有一个提供实时数据的成像系统能够传递信息来治理水质，将对了解水体现状有很大的帮助。此外，如果能够建立一个适当的预测水系统，将有助于更好地了解水的浊度特征。

提出的方法

1）构建一个基于预测的成像系统，该成像系统应包含两个主要功能：（1）传输图像数据以计算浊度的能力，（2）建立预测水系统以监测水库中的浊度的能力。

2）构建两个神经网络系统，一个人工神经网络系统(常规无雨时间)，其中RNN2系统用于子程序(考虑下雨时间)，以使用水传感器预测浊度值。由于下雨时间的发生，预测可能会有很大的误差，但我们的子程序可以调整结果的准确性。本研究提出了一种使用RNN2模型的深度学习方法，通过在正常时间运行主程序来预测时间序列数据。也就是说，当数据急剧增加时，子例程将自动运行。这项工作的主要目标是设计一个模型，该模型不仅可以预测下一步，还可以生成一系列预测，并利用多个驾驶时间序列以及一组静态(标量)特征作为其输入。

研究使用的方法

神经网络（NN）

神经网络是基于人类大脑的结构构建的，提供了一个简化的数学模型来解决各种非线性问题。以往的研究表明，人工神经网络模型的预测精度高于其他常规模型，如线性模型、非线性模型和模糊逻辑模型。传统的神经网络模型包括输入层、隐藏层和输出层，以及神经元、权值、偏置和激活函数等辅助成分。输入层可以接收来自信号或数据的输入值，隐层对输入值进行分析。输出层从隐藏层收集数据并决定输出。在学习过程中，神经网络修改其结构以获得与监督器相同的参考点或设定点。训练过程不断重复，直到神经网络输出和监督器之间的差异在一个可接受的范围内。

递归神经网络（RNN1）

RNN模型按元素处理序列数据，并保留一种状态来表示时间步长的信息。传统的神经网络假设输入向量的所有单元是独立的。因此，传统的神经网络对于序列数据的预测是无效的。RNN的架构包括三个主要组成部分(输入、隐藏神经元和激活函数)。之前的隐藏状态(ht)可以表示为

，其中为时刻的输入，为时刻的隐藏神经元，为隐藏层的权值，为隐藏层的过渡权值。当当前和以前的输入经过函数时，输入和以前的隐藏状态结合起来产生信息。然后，输出是新的隐藏状态，作为神经网络的记忆，因为它保存了来自前一个网络的信息。训练正则RNN会导致一系列梯度消失和爆炸问题。对于爆炸梯度，问题在反向传播后得到解决，反向传播在某一点上是封闭的。然而，结果可能不是最优的，因为所有的权重都没有更新。对于梯度消失的情况，可以通过初始化权值来调整，以减少梯度消失的可能性

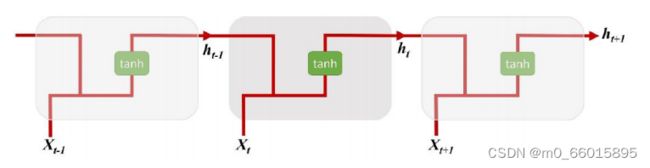
递归神经网络（RNN2）

递归神经网络是一种深度学习神经网络，它通常是通过递归地对输入的结构化数据应用相同的权重集来创建的，如下图所示。然后，它通过按拓扑顺序遍历给定的结构，在可变大小的输入结构上生成结构化预测，或者在其上生成标量预测。递归神经网络有时缩写为RNN2，已经成功地解决了学习序列数据中的预测问题，在学习自然语言处理中的序列和树结构方面已经取得了成功。RNN2最初被引入来学习结构的分布式表示，比如逻辑项。

尽管递归神经网络(RNN2)模型在系统鲁棒性和时间序列数据计算方面具有优势，但它们已被广泛应用于冗余数据优化。现有的RNN2模型存在局部最小值问题，且不具备规划完备性。因此，在时间序列数据采集中，需要采用多种技术来解决冗余数据。递归神经网络通常在任何层次结构上运行，将子表示转换为父表示。一般使用随机梯度下降(SGD)来训练这类网络，梯度是通过时间序列对变化数据进行反向传播来计算的。具体就是给定层中的每个节点通过定向(单向)连接连接到下一个连续层中的每个其他节点，每个节点(神经元)具有时变的实值激活，每个连接(突触)都有一个可以修改的实值权重，节点可以是输入节点(从外部网络接收数据)、输出节点(产生结果)或隐藏节点(在从输入到输出的过程中修改数据)。

 研究分析的步骤

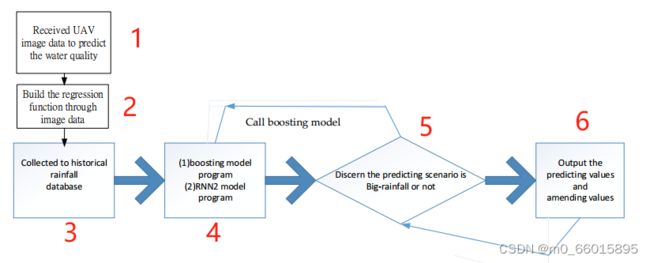
1. 无人机在传感器处拍摄图像获取水体的波段值，接收到的无人机图像数据预测水质；
2. 通过图像数据建立回归模型，然后根据从样本中获得的数据估计函数的参数。这样做的目的是将数据的图像波段呈现出来，形成水体浊度的相关性。
3. 收集到历史雨量数据库
4. 使用递归神经网络来分析时间序列浊度数据，本文的新颖之处在于我们使用了两个神经网络系统：

   (1)用于处理无雨时间的常规递归神经网络；(2)用于处理雨天的增量模型(RNN2)。

5. 判别预报情景是否为大暴雨，如果是大暴雨则使用RNN2模型。

6. 输出预测值和修正值

研究实验

数据集

本研究计划使用所选研究区域在无云天气的上午10点采集的图像数据作为标准图像格式，要求扫描高度高于地面15 m，视场40◦，以获得地面分辨率为0.4 m的图像。时间序列数据至少记录了72个时间间隔(位置参见图中的A、B、C点)，作为识别图像特征的元素，并在后续步骤中进行预测。

评估指标

1. 均方根误差(RMSE)：均方根误差是一种常用的测量方法，用于估计者预测的值与观察到的值之间的差异。
2. 平均绝对误差(MAE)：是用绝对值衡量成对观测值之间的误差。
3. R2：是一种统计度量，表示因变量的方差比例
4. 变异系数（CV）：是数据序列中数据点围绕平均值的相对离散度的统计度量。

实验目的

使用鲁棒深度学习模型来分析时间序列数据，使用输入数据、预测水平和训练时间，根据评价指标比较所选模型的精度，以预测库区浊度的水质。

实验内容

1）使用图像数据构建回归函数。

在第一阶段目标是监测水的浊度，本研究采用多元回归分析预测水质浊度值。B、G、R和IR是从图像数据中获取的四个变量，图像由无人机拍摄。从传感器b中提取浊度值，得到一系列回归函数。其中一个可表示为，其中T为浊度。部分回归误差绘制如下所示，其中y轴为浊度的真实值，x轴为回归预测值，平均误差约为0.07%。

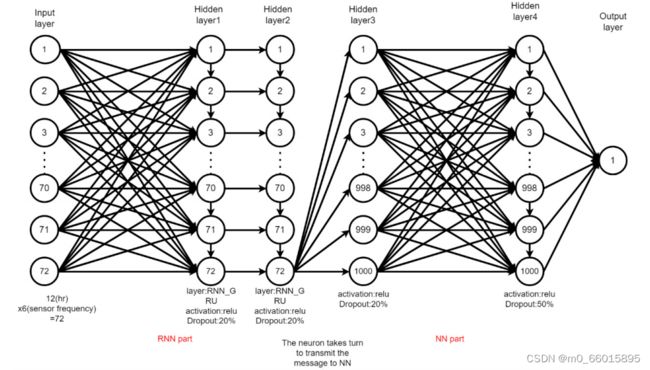
2）利用浊度时间序列数据建立RNN2模型

RNN2模型架如下所示构是基于神经网络框架构建的，有一个神经元输入层和一个神经元输出层。构造了四个隐藏层用于计算。两个部分构造为RNN2部分和NN部分。在考虑浑浊度的情况下，共设置了72个神经元输入来接收水质信号。第2层是隐藏层，该层接收到的神经元轮流将数据传输给神经网络。输入神经元72个，每小时采样6次。选择了四个隐藏层，前两个隐藏层位于RNN部分，后两个隐藏层连接到NN部分。为了加速和考虑网络的收敛速度，使用与输入层相同数量的神经元。采用整流线性单元(ReLu)作为激活函数，用于计算神经网络和RNN系统的核心。由于ReLu将所有负和零输入值转换为零，因此是合理的。drop - ratio为20%，设置在前三层。最后一个隐藏层设置为50%，以加速迭代的收敛。

实验结果

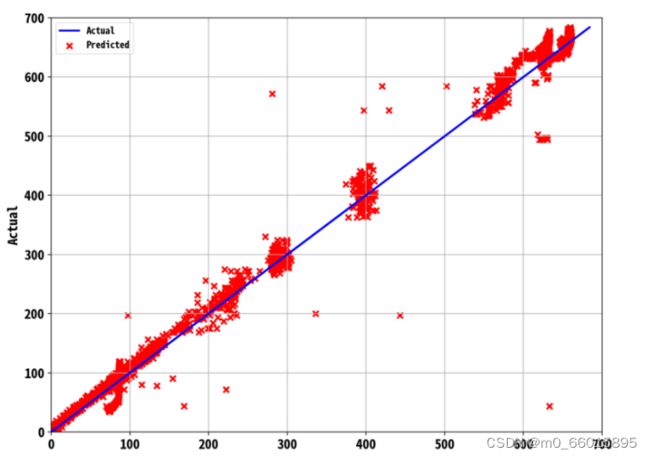
本研究收集了2019年10月的训练数据。针对累积雨量等于0和累积雨量大于0两种情况，建立了RNN2模型。训练数据集占整个数据集的0.7%，剩余部分作为测试数据集用于模型的自我测试。预测误差分布图如下所示。

模型性能

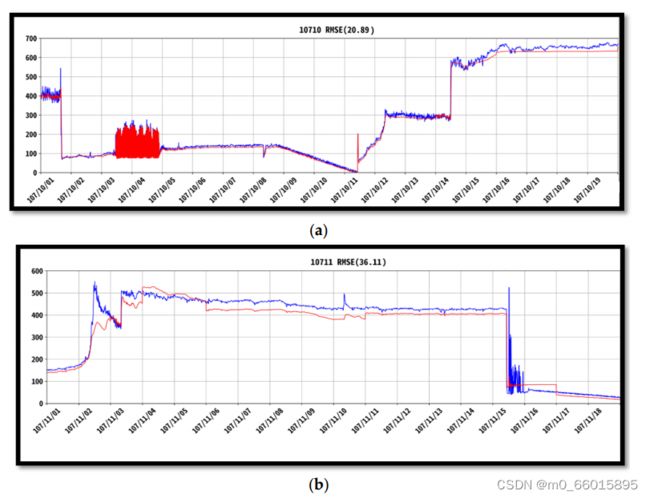
采用时程分析方法分析RNN2模型的性能，因此水的浊度可以应用RNN2对时间数据进行逐步分析。在我们的研究中，提取了一部分数据来显示分析的物理意义。x轴是时间和日期，y轴是浊度密度。使用2018年10月构建RNN2模型，图（a）图（b）分别显示了2018年10月和11月真实数据（蓝色）和预测（红色）的时程差异。10月均方根误差为20.89，小于11月(36.11)。这是因为预测结果更大，然而，10月和11月之间的差异足够小，不足以解释对结果的预测，这些预测被认为是相当理性的。

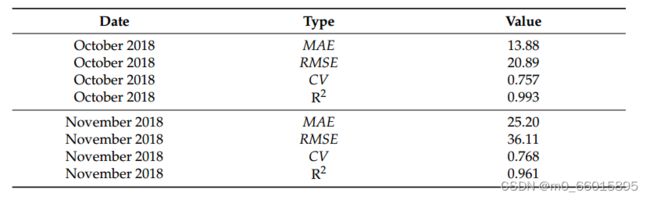
除了使用时程分析外，我们还使用了MAE、RMSE、CV和R2来观察模型的性能和准确性。十月表示用于生成RNN2模型的训练数据，十一月表示验证部分，使用测试数据检查如何显示实时值。均方根误差是用来比较抽样数据的准确性，在训练模型中，训练数据的RMSE为20.89，测试数据的RMSE为36.11。RNN2模型预测的r平方值分别为0.993(训练数据)和0.961(测试数据)。分析表明，在不同的分析条件下，这些模型各有优缺点。RNN2显示了关于均方根误差(RMSE)评估度量的性能，最重要的发现是RNN2模型适用于水质的准确预测。

研究结论

递归神经网络(RNN2)是一种利用时间序列数据对几个前向阶跃数据项进行预测的人工神经网络。这种深度学习算法通常是为时间问题设计的。此外，改进RNN利用训练数据来学习一个学习系统，这类似于它的“记忆”，它从之前的输入中获取信息来影响当前的输出。传统的深度神经网络假设输入和输出是相互独立的，而循环神经网络的输出依赖于序列中的先验元素。当未来事件有助于确定给定序列的输出时，单向递归神经网络无法在其预测中考虑这些事件。考虑到RNN2的这些特点，利用RNN2对水组分的小步时间序列数据进行解析可以成功应用。

SVM-解决线性不可分问题

在上周周报中学习了SVM用来解决二元线性分类问题，即对于线性可分的情况，通过SVM总能找到一个超平面严格地将数据分成两类，但是那么对于线性不可分（非线性）情况，不能严格地划分类别，将两类数据分开，因为总有一些数据分类是错误的，或者落在间隔内，这些数据点称为异常点。而训练SVM的最终目标就是训练出来一个线性分类器，不仅能处理线性可分的数据，而且还能解决线性不可分的数据。 解决线性不可分的情况有两种基本的思路：

思路一：引入松弛变量和惩罚因子

上图描述了两种情况：①错误分类（也称大离差）：黑点中出现了一个白点；②超平面间隔不是最优（小离差）：在最大间隔内部出现了一个异常点，这个点不知道属于哪类。对于这两种情况，勉强可认为数据在大体上还是线性可分的，因此我们只需要将约束条件放宽或者缩小最大间隔即可。

超平面公式求解

其中松弛变量代表对应的数据点运行偏离的几何间隔的量；

软误差：指所有数据元组的松弛变量的和；
惩罚因子是一个大于0的系数（一般记为C），它的加入法则是：软误差乘以该系数后，加入目标函数中，使之称为新的目标函数。是用于控制目标函数在 “寻找最大间隔的超平面” 和 “保证数据点偏差量最小” 两者中找到平衡的一个权重参数，是一个确定的常量。

这里对的求解，需要借助SMO算法，即序列最小化优化算法（Sequential Minimal Optimization，SMO）是专门用来求解多参数的对偶问题的，这是一种高效的解决方案，其核心思想是：每次只优化一个参数，其他参数先固定，只求当前这个参数的极值。下面一步步进入算法的思想。

思路二：低维映射到高维

如何划分非线性数据

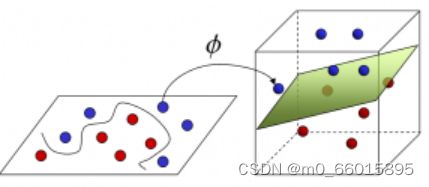
对于下图中左边的蓝色和红色的点，我们是没办法找到一条直线完全将两者分开的，但是我们可以找到一条曲线将他们分开，但如果将这个二维数据映射到三维空间中，我们是可以找到一个平面来分开它们的。因此将低维数据（线性不可分）映射到高维空间中，可以使得在高维空间中数据是线性可分的。

 核函数

一些线性不可分的问题可能是非线性可分，即特征空间存在超曲面（hypersurface）能将正类和负类分开。使用非线性函数可以将非线性可分问题从原始的特征空间映射至更高维的希尔伯特空间（Hilbert space） ，从而转化为线性可分问题。核函数是可以将原始输入空间映射到新的特征空间，从而使得原本线性不可分的样本可能在核空间可分。

直观理解核函数就是内积，是用来计算映射到高维空间之后的内积的一种简便方法，所以它能减少高维空间内积的计算量，这里有个很容易混淆的点，核函数并不是用来映射的，而是用来计算内积的。常见的核函数有：

名称	表达式
多项式核（polynomial kernel）
径向基函数核（RBF kernel）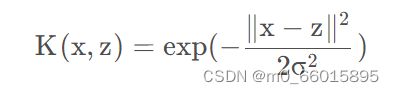
拉普拉斯核（Laplacian kernel）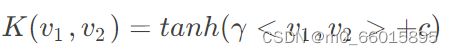
Sigmoid核（Sigmoid kernel）