c++利用哈夫曼编码实现文件的压缩加密和解压缩解密
- 需求分析
@1:编码实现哈夫曼树,然后根据数据建立哈夫曼树,然后显示所有的字符的哈夫曼编码
@2:实现哈夫曼编码和解码 并通过编码实现文本文件的压缩 通过解码实现压缩文件的解压缩
- 概要设计
@1:在二叉树的基础上实现哈夫曼树的数据结构
@2:读取文本文件-->对字符频度进行统计-->构建哈夫曼树-->进行哈夫曼编码-->通过哈夫曼编码将文本文件压缩输出到压缩文件中
- 详细设计
@1:哈夫曼树的实现以及哈夫曼编码:
哈夫曼树的是是实现思路:
给定一个字符集合,统计字符出现的频率,并按照频率从小到大排序。取出频率最小的两个字符,将它们作为叶子节点构建一棵二叉树(可以使用任意一种二叉树表示方式,比如孩子兄弟表示法)。以该二叉树为基础,再次取出频率最小的两个字符,将它们添加到这棵二叉树中(作为兄弟或者作为父节点的左右孩子),得到一棵较大的二叉树。重复上述步骤,直到所有字符都被添加到二叉树中。此时,生成的二叉树即为哈夫曼树。根据哈夫曼树的构建规则,左子树代表频率较小的字符,右子树代表频率较大的字符。对于每一个叶子节点,记录其路径所代表的二进制编码即为该字符的哈夫曼编码。
@2:哈夫曼编码器和解码器是实现文本文件的压缩和解压缩
编码器实现压缩文件:
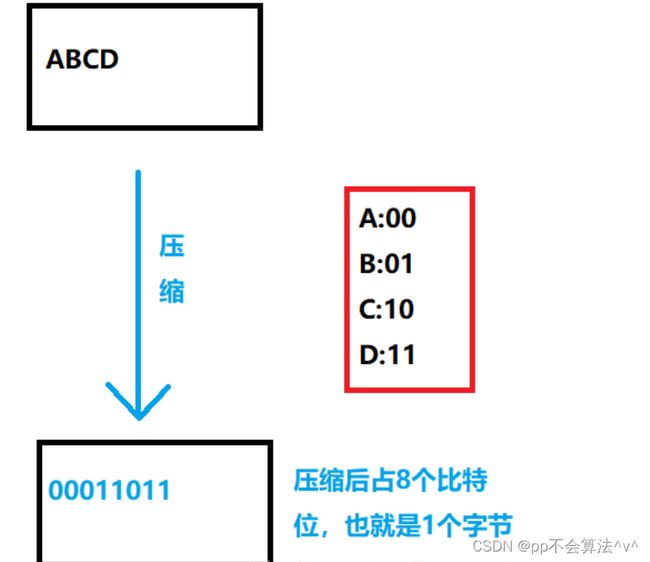
压缩原理:字符频度越大的字符的哈夫曼编码越短 那么就可以用哈夫曼编码来替换原字符的编码 从而实现解压缩,大致如下图:
压缩的流程:
首先一个字符一个字符的读取待压缩文件 统计字符的种数以及字符出现的频度
为了解压缩时重构哈夫曼树 所以此时要将字符的出现的字符种数,字符以及相应的频度写入待压缩文件 然后紧接着写入压缩文件的长度
然后根据字符以及字符频度创建哈夫曼树 进行哈夫曼编码
然后以二进制的方式一个一个字节地遍历待压缩文件 准备一个中间空字符tempchar和计数器num 匹配每个字节对应的哈夫曼编码
然后通过遍历哈弗编码进行位操作每遍历一位哈夫曼编码就将tempchar左移一位 num自增1 如果当前哈夫曼编码是1就将tempchar|1 ,当num=8的时候将tempchar写入压缩文件 ,然后将tempchar 和num复原继续遍历哈夫曼编码,直到遍历完待压缩文件,如果最后的哈夫曼编码不足8位那么就在后面补0 补齐8位
解压缩流程:
首先从压缩文件种读取字符以及字符频度重构哈弗曼树 然后读取文件长度并记录
然后一个字节一个字节地遍历压缩文件之后的字符 ,从根节点出发,并且对每个字节的每一位通过位运算遍历 如果是1 移动到有孩子 如果是0就移动到左孩子 只要判断移动到了叶子结点 就将叶子节点对应的字符写入到解压缩之后的文件中,
项目效果演示:
主界面:
功能1展示:
功能2展示:
功能3展示:
压缩加密后:
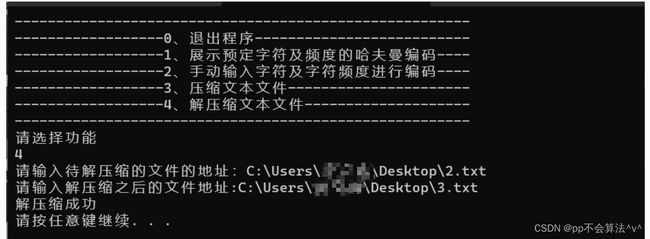
功能4展示:
将上面压缩加密后的文件2.txt解密解压缩:
项目结构展示:
好了现在直接上代码:
哈夫曼树.h:
#pragma once
#include
#include
using namespace std;
struct frequence{// 用来储存字符频度
unsigned char uchar; // 以8bits为单元的无符号字符(0~255)
unsigned long frequency; // 每类(以二进制编码区分)字符出现频度(频度可能较大 所以用char不够)
frequence(unsigned char x = 0, unsigned long y = 0) :uchar(x), frequency(y) {};
};
struct node {//哈夫曼树结点结构体
unsigned char uchar;//八位无符号字符
unsigned long weight;//权值(出现的频度)
char* hufcode;//哈夫曼编码
int Lchild;//左孩子
int Rchild;//右孩子
int parent;//双亲
node(int x = -1, int y = -1, int z = -1, int w = -1) :weight(x), Lchild(y), Rchild(z), parent(w) {};
};
void select(node* tree, int k, int& p1, int& p2) {
// 初始化指针
p1 = -1, p2 = -1;
// 在还parent=-1的结点中查找权值最小和次小的两个结点
for (int i = 0; i < k; ++i) {
if (tree[i].parent != -1) continue; // 非叶子结点跳过
if (p1 == -1 || tree[i].weight < tree[p1].weight && tree[i].weight>0) {
p2 = p1;
p1 = i;
}
else if (p2 == -1 || tree[i].weight < tree[p2].weight && tree[i].weight>0) {
p2 = i;
}
}
}
class HuffmanTree {
public:
HuffmanTree(int n, frequence* a);//构造函数构造哈夫曼树 n是叶子结点的个数 a是叶子结点权值的数组
~HuffmanTree();
void print();
void printHuffcode();
void huffcodeing();//哈夫曼编码
public:
int n;//叶子结点个数
int m;//结点总个数
node* tree;
node* root;
//char** Huffcode;
};
inline HuffmanTree::HuffmanTree(int n, frequence* a)
{
this->n = n;
this->m = 2 * n - 1;
tree = new node[m];
root = &tree[m - 1];
for (int i = 0; i < n; i++)
{
tree[i].weight = a[i].frequency;
tree[i].uchar = a[i].uchar;
}
for (int i = n; i < m; i++)//构造哈夫曼树
{
//首先选出parent=-1 的结点中权值最小的两个结点
int p = -1, q = -1;
select(tree, m, p, q);
tree[i] = node(tree[p].weight + tree[q].weight, p, q);
tree[p].parent = i;
tree[q].parent = i;
}
huffcodeing();
}
inline HuffmanTree::~HuffmanTree()
{
if (tree)
delete[]tree;
}
inline void HuffmanTree::print()
{
for (int i = 0; i < n; i++)
cout << "父节点:"<
#include//读写文件的头文件
#include"哈夫曼树.h"
#define _CRT_SECURE_NO_WARNINGS // 如果没有定义这句话会可能会有编译错误
//压缩文件
//压缩的思路
//1、首先一个一个字符读取要压缩的文件 统计字符的种数以及出现的频度
//2、用上面统计的数据构造哈夫曼树 进行哈夫曼编码
//3、然后再一个一个字符地遍历要压缩的文件找到哈夫曼树中对应的叶子结点的哈夫曼码 然后用一个中间空字符 然后通过位操作将哈夫曼码转为二进制数存入中间字符 如果满了八位就写入文件 没有就继续读取下一个字符
//4、由于哈夫曼中的编码是权值越大的哈夫曼码越短 所以就实现了数据的压缩
void compress(std::string inputFilename, std::string outputFilename)
{
int i, j;
unsigned int char_kind = 0;
//暂存8bits字符
unsigned char temporary_char;
unsigned long file_length = 0;//文件的总字符数
FILE* input_file, * output_file;
frequence temporary_node;
unsigned int number_node;
//待存编码缓冲区
char code_the_buffer[256] = "\0";
unsigned int bit_count = 0;//用于记录写入是不足八位 的哈夫曼码的长度
/*
** 动态分配256个结点,暂存字符频度,
** 统计并拷贝到树结点后立即释放
*/
frequence* temporary_char_frequency = (frequence*)malloc(256 * sizeof(frequence));//用于统计的中间静态数组
//初始化暂存结点
for (i = 0; i < 256; ++i)
{
temporary_char_frequency[i].frequency = 0;
//数组的256个下标与256种字符对应
temporary_char_frequency[i].uchar = (unsigned char)i;
}
//首先遍历待压缩文件 统计字符的种数和出现的频度
//以二进制只读的方式打开待压缩文件
fopen_s(&input_file,inputFilename.c_str(), "rb");
if (input_file == nullptr)
{
cout << "未找到待压缩文件" << endl;
return;//直接退出函数
}
//读入一个字符
fread((char*)&temporary_char, sizeof(unsigned char), 1, input_file);
while (!feof(input_file))
{
//统计下标对应字符的权重,利用数组的随机访问快速统计字符频度
++temporary_char_frequency[temporary_char].frequency;
++file_length;
//读入一个字符
fread((char*)&temporary_char, sizeof(unsigned char), 1, input_file);
}
std::fclose(input_file);
//对频度统计数组 temporary_char_frequency按照频度做降序排序
std::sort(temporary_char_frequency, temporary_char_frequency + 256, [&](frequence a, frequence b) {
return a.frequency > b.frequency;
});
// 统计实际的字符种类(出现次数不为0)
for (i = 0; i < 256; ++i)
{
if (temporary_char_frequency[i].frequency == 0)
{
break;
}
}
char_kind = i;
//如果只有一种字符那么就要特殊处理 因为不能进行哈夫曼编码 那么就只要写入字符的种数 这个字符 然后写入这个字符的个数就行了
if (char_kind == 1)
{
//打开压缩后将生成的文件
fopen_s(&output_file,outputFilename.c_str(), "wb");//以二进制只写的方式打开压缩文件
//写入字符种数(因为一种字符和多种字符的解码方式不同 所以要写入字符的种数 方边解码的时候选择解码的方式)
fwrite((char*)&char_kind, sizeof(unsigned int), 1, output_file);
//写入唯一的字符
fwrite((char*)&temporary_char_frequency[0].uchar, sizeof(unsigned char), 1, output_file);
//写入字符频度,也就是文件长度
fwrite((char*)&temporary_char_frequency[0].frequency, sizeof(unsigned long), 1, output_file);
free(temporary_char_frequency);
std::fclose(output_file);
}
else
{
HuffmanTree huffman_tree(char_kind, temporary_char_frequency);//构造哈夫曼树 进行哈夫曼编码(向左一步位0 有一步为1
//释放字符频度统计的暂存区
free(temporary_char_frequency);
//写入字符和相应权重,供解压时重建哈夫曼树
//打开压缩后将生成的文件
fopen_s(&output_file,outputFilename.c_str(), "wb");//以二进制只写的方式打开压缩文件
//写入字符种类
fwrite((char*)&char_kind, sizeof(unsigned int), 1, output_file);
for (i = 0; i < char_kind; ++i)
{
//写入字符(已排序,读出后顺序不变)
fwrite((char*)&huffman_tree.tree[i].uchar, sizeof(unsigned char), 1, output_file);
//写入字符对应权重
fwrite((char*)&huffman_tree.tree[i].weight, sizeof(unsigned long), 1, output_file);
}
//紧接着字符和权重信息后面写入文件长度和字符编码
//写入文件长度
fwrite((char*)&file_length, sizeof(unsigned long), 1, output_file);
//以二进制只读的方式打开待压缩文件 遍历每一个字节
fopen_s(&input_file,inputFilename.c_str(), "rb");
char _char = '\0';
while (fread(&temporary_char, sizeof(unsigned char), 1, input_file) == 1)
{
//匹配哈夫曼码
string code;
for (int o = 0; o < char_kind; o++)
{
if (huffman_tree.tree[o].uchar == temporary_char)
{
code = huffman_tree.tree[o].hufcode;
break;
}
}
//以八位(一个字节)为单位处理哈夫曼码
for (int p = 0; p < code.length(); p++)//当哈夫曼码大于8个字符的时候
{
_char <<= 1;//左移一位腾出一个bit
if (code[p] == '1')
_char |= 1;
bit_count++;
if (bit_count == 8)//满八位
{
fwrite((char*)&_char, sizeof(unsigned char), 1, output_file);//写入压缩文件
bit_count = 0;
_char = '\0';
}
}
}//读文件的循环
//最后如果还剩下一个哈夫曼码没有写入 那就补齐八位写入(将已经写进的哈夫曼码移到高位)
if (bit_count > 0 && bit_count < 8)
{
_char <<= (8 - bit_count);
fwrite((char*)&_char, sizeof(unsigned char), 1, output_file);//写入压缩文件
}
std::fclose(input_file);//关闭文件
std::fclose(output_file);
}
}
---------------------------------------------------------------------------------------
decompress.h:
#pragma once
#include"哈夫曼树.h"
#include
#include
//哈夫曼解码解压缩文件
void decompress(string inputFilename, string outputFilename)
{
unsigned int i;
unsigned long file_length;
//控制文件写入长度
unsigned long file_write_length = 0;
FILE* input_file, * output_file;
//存储字符种类
unsigned int char_kind;
unsigned int number_node;
//暂存8bits编码
unsigned char temporary_char;
//保存根节点索引,供匹配编码使用
unsigned int root;
//以二进制方式打开压缩文件
fopen_s(&input_file,inputFilename.c_str(), "rb");
if (input_file == NULL)
{
return;
}
//读取压缩文件前端的字符及对应编码,用于重建哈夫曼树
//读取字符种类数
fread((char*)&char_kind, sizeof(unsigned int), 1, input_file);
number_node = 2 * char_kind - 1;
if (char_kind == 1)
{
//读取唯一的字符
fread((char*)&temporary_char, sizeof(unsigned char), 1, input_file);
//读取文件长度
fread((char*)&file_length, sizeof(unsigned long), 1, input_file);
//打开压缩后将生成的文件
fopen_s(&output_file,outputFilename.c_str(), "wb");
while (file_length--)
{
fwrite((char*)&temporary_char, sizeof(unsigned char), 1, output_file);
}
std::fclose(input_file);
std::fclose(output_file);
}
else
{
frequence* frequencearry = new frequence[char_kind];
for (i = 0; i < char_kind; ++i)
{
//读入字符
fread((char*)&frequencearry[i].uchar, sizeof(unsigned char), 1, input_file);
//读入字符对应权重
fread((char*)&frequencearry[i].frequency, sizeof(unsigned long), 1, input_file);
}
//重构哈夫曼树
HuffmanTree huffman_tree(char_kind, frequencearry);
cout << "重建后的哈夫曼树:" << endl;
//huffman_tree.print();
//cout << "-----------------------------------------------------" << endl;
//读完字符和权重信息,紧接着读取文件长度和编码,进行解码
//读入文件长度
fread((char*)&file_length, sizeof(unsigned long), 1, input_file);
//打开压缩后将生成的文件
fopen_s(&output_file,outputFilename.c_str(), "wb");
root = number_node - 1;
while (1)
{
//读取一个字符长度的编码(8位)
fread((char*)&temporary_char, sizeof(unsigned char), 1, input_file);
//处理读取的一个字符长度的编码
for (i = 0; i < 8; ++i)
{
//由根向下直至叶节点正向匹配编码对应字符
if (temporary_char & 128)//0 向左走
{
root = huffman_tree.tree[root].Rchild;
}
else//1 向右走
{
root = huffman_tree.tree[root].Lchild;
}
if (root < char_kind)//走到了叶子结点
{
fwrite((char*)&huffman_tree.tree[root].uchar, sizeof(unsigned char), 1, output_file);
//cout << "写入的第" << file_write_length +1<< "个字符为:" << huffman_tree.tree[root].uchar << endl;
++file_write_length;
//控制文件长度,跳出内层循环
if (file_write_length == file_length)
{
break;
}
//复位为根索引,匹配下一个字符
root = number_node - 1;
}
//将编码缓存的下一位移到最高位,供匹配
temporary_char <<= 1;
}
//控制文件长度,跳出外层循环
if (file_write_length >=file_length)
{
break;
}
}
//关闭文件
std::fclose(input_file);
std::fclose(output_file);
}
}
---------------------------------------------------------------------------------------
main.cpp:
#include
#include
#include"哈夫曼树.h"
#include"compress.h"
#include"decompress.h"
#include
using namespace std;
void showMenu()
{
cout << "-------------------------------------------------------" << endl;
cout << "------------------0、退出程序--------------------------" << endl;
cout << "------------------1、展示预定字符及频度的哈夫曼编码----" << endl;
cout << "------------------2、手动输入字符及字符频度进行编码----" << endl;
cout << "------------------3、压缩文本文件----------------------" << endl;
cout << "------------------4、解压缩文本文件--------------------" << endl;
cout << "-------------------------------------------------------" << endl;
}
int main()
{
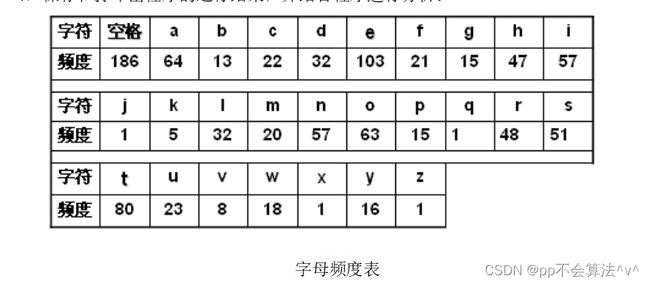
frequence fre[27]{ frequence(' ',186),frequence('a',64), frequence('b',13), frequence('c',22),
frequence('d',32), frequence('e',103), frequence('f',21), frequence('g',15), frequence('h',47),
frequence('i',57), frequence('j',1), frequence('k',5), frequence('l',32), frequence('m',20),
frequence('n',57), frequence('o',63), frequence('p',15), frequence('q',1), frequence('r',48),
frequence('s',51), frequence('t',80), frequence('u',23), frequence('v',8), frequence('w',18),
frequence('x',1), frequence('y',16), frequence('z',1) };
HuffmanTree huftree(27, fre);
int n = 0;
while (1)
{
showMenu();
cout << "请选择功能" << endl;
cin >> n;
switch (n)
{
case 0:
{
cout << "欢迎下次使用!!!" << endl;
return 0;
}
case 1:
{
cout << "对预定字符及频度进行哈夫曼编码之后结果为:" << endl;
cout << "---------------------------------------------------" << endl;
huftree.printHuffcode();
cout << "---------------------------------------------------" << endl;
system("pause");
break;
}
case 2:
{
int num = 0;
cout << "请输入字符种数" << endl;
cin >> num;
char uchar;
int frequ = 0;
frequence* freq = new frequence[num];
for (int i = 0; i < num; i++)
{
cout << "请输入字符和频度" << endl;
cin >> uchar >> frequ;
freq[i] = frequence(uchar, frequ);
}
HuffmanTree tr(num, freq);
cout << "编码结果为:" << endl; cout << "对预定字符及频度进行哈夫曼编码之后结果为:" << endl;
cout << "---------------------------------------------------" << endl;
tr.printHuffcode();
cout << "---------------------------------------------------" << endl;
system("pause");
break;
}
case 3:
{
string inputFileName, outputFileName;
cout << "请输入待压缩的文件的地址:";
cin >> inputFileName;
cout << "请输入压缩之后的文件地址:";
cin >> outputFileName;
compress(inputFileName, outputFileName);
cout << "压缩成功" << endl;
system("pause");
break;
}
case 4:
{
string inputFileName, outputFileName;
cout << "请输入待解压缩的文件的地址:";
cin >> inputFileName;
cout << "请输入解压缩之后的文件地址:";
cin >> outputFileName;
decompress(inputFileName, outputFileName);
cout << "解压缩成功" << endl;
system("pause");
break;
}
default:
{
cout << "您的输入有误!!!" << endl;
system("pause");
break;
}
}//switch
system("cls");
}//while
return 0;
}