基于Boosting的力扣题目建模分析

1 背景介绍

随着大数据、人工智能等技术的发展和数字化转型提速，“数字人才”需求旺盛。《产业数字人才研究与发展报告（2023）》显示，我国目前数字人才缺口达到2500万-3000万。力扣是一个代码在线评测平台，提供多种不同算法和数据结构的编程题目，帮助用户训练算法思维和编程能力，在求职者中备受欢迎。

为了解力扣题目难度与热度的影响因素、实现难度自动分级，本案例基于Boosting模型分析题目内容、公司标签、题目标签等特征与题目难度、题目提交量的关系。

2 数据说明

本案例从力扣题库中抓取除会员专享题目外所有题目信息共2635条，对于题目难度的分类问题，因变量为是否为简单题；对于题目提交量的回归分析，因变量为题目提交量。自变量共10个字段，可分为题目内容、题目标签和公司标签共三个类别。字段说明见表1：

表1 数据字段说明表

3 描述性分析

3.1 分类问题描述性分析

首先，我们对题目难度的分类问题进行描述性分析。

考虑因变量题目难度的分布情况，力扣的题目难度标签有EASY/MEDIUM/HARD三种。定义EASY变量，将难度标签中的MEDIUM和HARD分类合并置为0，EASY分类置为1，作为本案例的二分类标签。分别绘制柱形图如下，柱形图显示力扣题库中MEDIUM题型占比最高，共1349条；简单题占比为27.55%，表现出类别不平衡性。

图1 题目难度分布柱形图

接下来探索是否为简单题与自变量间的相关关系。对于题目内容特征，绘制是否为简单题下对数题目要求文本长度、对数提示信息文本长度分布箱线图。从分组箱线图中可以看出，非简单题的题目要求和提示文本长度明显高于简单题。示例能够帮助用户理解题目要求，是题目的重要组成部分，绘制示例个数的百分比堆积柱形图，题目大部分提供2到3个示例，而简单题中1个示例的占比更高。

图2 题目内容特征分布

绘制题目要求文本词云图。高频词主要涵盖数据结构和计算要求两方面，比如"数组"“字符串”“矩阵"和"查询”“顺序”"最小"等词组。

图3 题目要求文本词云图

接下来考虑题目标签和是否为简单题的相关关系，题目标签分为基本、算法、基础数据结构、高级数据结构、技巧、数学和其他共七种分类，每个大类中覆盖多个知识点。绘制分类标签总数量的直方图、分类标签总数量与是否为简单题的百分比堆积柱形图。可以看出，平均一个题目具有3个一级分类。随着分类标签增多，题目中简单题占比下降，难度伴随考察范围的扩大而升高。

图4 分类标签总数量分布

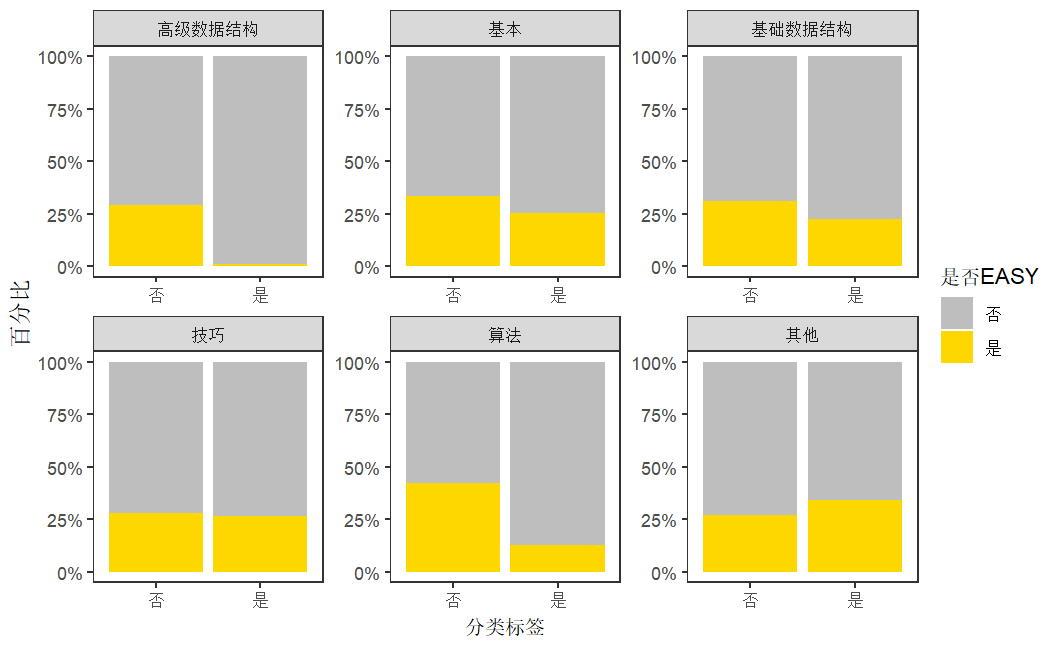
对于不同分类标签，分别绘制六种分类标签数量与是否为简单题的百分比堆积柱形图。柱形图显示，包含基本、算法、基础数据结构和高级数据结构标签的题目，与不含对应标签的题目相比简单题占比降低，特别是高级数据结构的题目中简单题比例低于5%，说明这一类型的题目具有高挑战性。而其他分类则简单题占比较高，可能是由于数据库、多线程和Shell等知识考察重视基础应用能力，对算法或数据结构等难度高的环节涉及较少。

图5 不同分类标签数量的百分比堆积柱形图

最后分析公司标签和是否为简单题的相关关系，公司标签柱形图显示，亚马逊、谷歌、字节跳动和微软的题目数量位于题目标签的前四名，占比远高于华为、腾讯等公司的题目。

图6 公司标签柱形图

绘制是否有公司标签与是否为简单题的百分比堆积柱形图，与没有公司标签的题目相比，包含公司标签的题目中简单题占比更低，公司面试题比普通练习题难度更高。对于不同公司标签，分别绘制谷歌、华为和腾讯三家公司分类标签与是否为简单题的百分比堆积柱形图。从堆积柱形图中可以看出，谷歌、华为公司的题目难度较高，而腾讯的题目难度则较低。

图7 公司标签百分比堆积柱形图

3.2 回归问题描述性分析

接下来，我们分析题目提交量的回归问题中所涉及变量的分布情况。

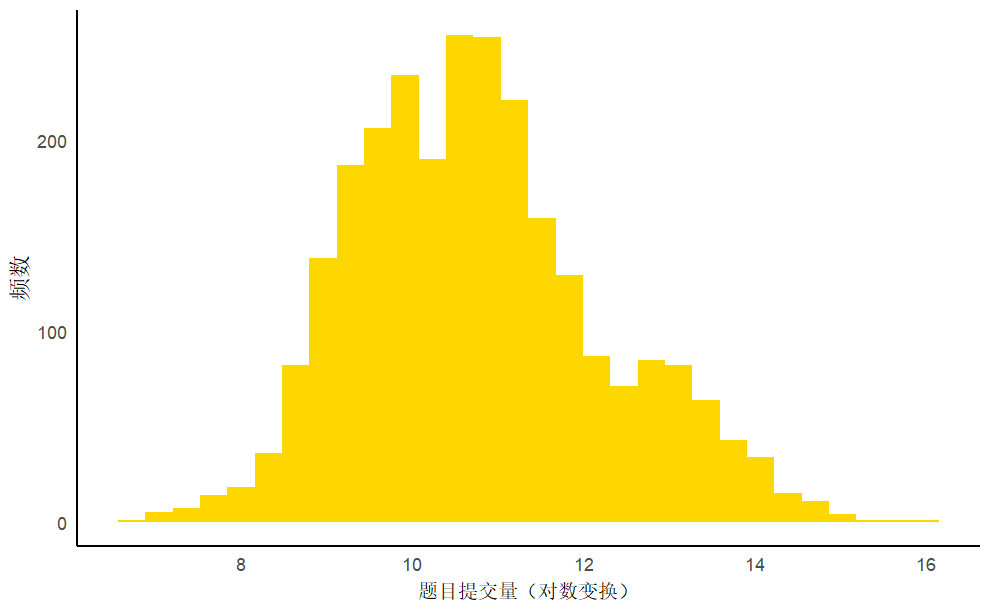
对于因变量题目提交量，直方图显示对数变换后的题目提交量符合正态分布，呈现一定程度的右偏分布，超过90%的样本处于7千到200万条提交量的区间中。

图8 题目提交量频数直方图

其次，探索题目提交量与自变量间的相关关系。对于题目难度，绘制不同难度下题目提交量分组箱线图。从分组箱线图中可以看出，题目提交量随着难度的上升而下降，三者中困难类型的题目平均提交量最低。

图9 不同难度题目提交量分组箱线图

绘制不同题目要求长度对应题目提交量分组箱线图。不同题目长度的平均提交量水平存在明显差别，题目要求长度集中于 50-200 个字符，整体上平均提交量随题目文本长度增加而下降。

图10 不同要求长度题目提交量分组箱线图

最后，对于公司标签，不同公司题目提交量分组箱线图显示，具有公司标签的题目提交量明显高于不具有公司标签的题目，其中特别是腾讯的题目提交量较高。

图11 不同公司题目提交量分组箱线图

4 建模分析

在本节中我们将介绍Boosting、AdaBoost以及提升树算法的基本原理、构建步骤以及R语言中对应的代码实现和结果解读。

4.1 Boosting概述

集成学习将多个弱分类器组合为强分类器，分为模型存在依赖关系的boosting和模型彼此独立的bagging两种类型。

Boosting可将弱学习器提升为强学习器，其工作机制为:

1. 从初始训练集训练出一个基学习器；

2. 根据基学习器的表现调整训练样本分布，使得先前基学习器做错的训练样本在后续受到更多关注；

3. 基于调整后的样本分布来训练下一个基学习器;

4. 重复上述步骤，直至基学习器数目达到事先指定的值，最终将这些基学习器进行加权结合。

4.2 AdaBoost算法

4.2.1 算法概述

AdaBoost算法是Boosting的一种代表算法，其基本思想是每一轮提高那些被前一轮弱分类器错误分类的样本的权值，降低被正确分类的样本的权值；最终通过加权多数表决的方法得到分类结果。接下来介绍构建AdaBoost的流程：

输入：训练数据集

输出：最终分类器

• 初始化权值分布

• 对

• 使用有权值分布的训练数据集学习，得到分类器(取值 {-1,1})

• 计算在训练数据集上的分类误差率：

• 计算的系数

• 更新训练数据集的权值分布，其中

• 令 ,最终得到分类器

4.2.2 算法实现

在R中可使用adabag包中的boosting()函数构建adaboost分类模型。可采用importance属性查看模型变量重要性，在力扣题目难度分类问题的AdaBoost模型中，分类标签中的要求文本长度和提示文本长度两项变量具有较高的相对重要性。

图12 AdaBoost分类模型变量重要性

4.3 提升树算法

4.3.1 算法概述

提升树算法是Boosting的另一种代表算法，它实际上是以决策树为基函数，采用加法模型与前向分步算法的集成算法。对于二分类问题，将AdaBoost的基本分类器设置为二类分类树；对于回归问题，采用平方损失函数，，即每一步优化拟合上一步残差。

然而，对于一般损失函数而言，每一步优化并不容易。Freidman提出了梯度提升算法，关键是利用损失函数的负梯度在当前模型的值：

，作为回归问题提升树算法中的残差近似值，拟合一个回归树。而采用决策树作为弱分类器的梯度提升算法被称为GBDT。

接下来，我们介绍构建GBDT的流程：

输入：训练数据集，损失函数

输出：最终回归树

• 初始化

• 对:

• 对，计算

• 对拟合回归树，得到第m棵树的叶节点区域；

• 对，计算；

• 更新

• 得到回归树：

此外，对于分类问题，GBDT的常用损失函数有两种：

• 采用指数损失函数，使GBDT算法退化为AdaBoost算法；

• 采用对数似然损失函数，即交叉熵，以类别的预测概率值和真实概率值的差拟合损失，，对应负梯度为

4.3.2 算法实现

在R中可使用gbm包中的gbm()函数构建GBDT模型，其中设置参数distribution，选择模型使用的分布函数，例如选择"gaussian"（平方误差）、“laplace”（绝对损失）、“bernoulli”（0-1结果的logistic回归）、“adaboost”（0-1结果的adaboost指数损失）等。在本案例中，对于力扣题目难度分类问题，以是否为“EASY”的二分类为因变量，选取分布函数为“bernoulli”；对于题目提交量回归问题，以题目提交量的对数为因变量，选取分布函数为“gaussian”。

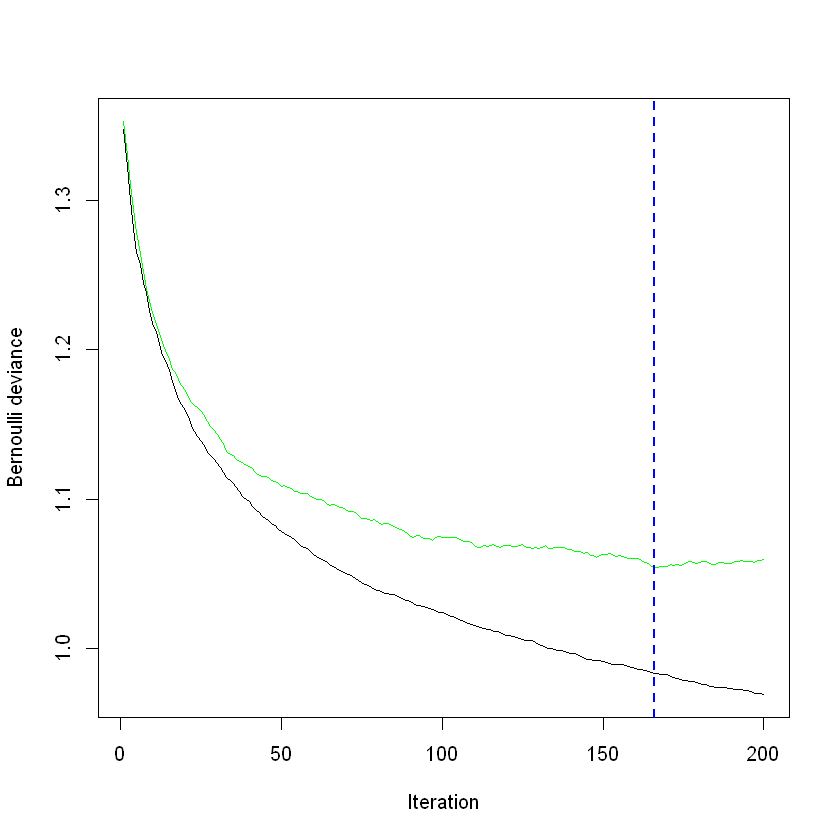
迭代次数是影响GBDT模型预测效果的重要参数，可使用gbm.perf()函数对迭代次数调参，其中参数"method"可从"OOB"（袋外估计）、“test”（测试集）或"cv"（交叉验证）中选择估计方法。随着迭代次数增加，力扣题目难度分类模型的Bernoulli Deviance下降情况如图13所示，其中黑线为训练集的损失，衡量模型在训练数据上的拟合程度；绿线为测试集的损失，衡量模型的泛化能力，蓝线则标注了最小的测试集损失对应的最优迭代次数。在分类模型中，选取“164”为最优的迭代次数。

图13 GBDT分类模型迭代次数调参

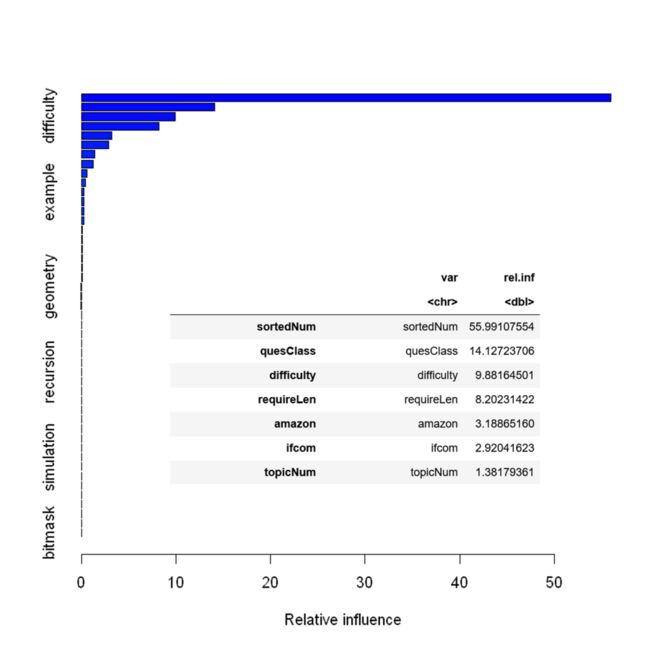
可使用summary.gbm()函数查看变量相对重要性。在力扣题目难度分类问题中，算法标签、分类标签总数量、要求文本和提示文本长度特征是重要变量；在力扣题目提交量的回归模型中，所属题库编号特征在回归模型中的变量重要性远高于其他特征。

图14 GBDT分类模型变量重要性

图15 GBDT回归模型变量重要性

5 总结

本案例介绍了Boosting的两种经典算法——AdaBoost算法和提升树算法的基本原理和构建流程，讲解了变量重要性等关键指标，并介绍了R语言中实现对应模型的方法。通过分组箱线图、堆积柱形图和词云图等分析题目内容、题目标签和公司标签等变量与题目难度、题目提交量的相关关系。以是否为简单题为因变量构建AdaBoost和GBDT分类模型、以题目提交量为因变量构建GBDT回归模型，探究力扣题目难度与热度的影响因素。

狗熊会特别感谢为本案例提供宝贵素材和为案例重新整理加工提供帮助的小伙伴：来自复旦大学的邵路婷。

本案例为狗熊会精品案例库收录。狗熊会精品案例库为狗熊会核心商业产品，目前收录了超过100个案例，包括探索性数据分析、回归分析、机器学习、文本分析、时间序列分析等模块，涉及电商、金融、餐饮等行业。狠戳阅读原文，查看狗熊会精品案例库。狗熊会精品案例库面向机构收费授权开放，有意洽谈者，请加熊二微信clubear2详细沟通。

点击此处“阅读全文”查看更多内容