LCT(link cut tree) 详细图解与应用

樱雪喵用时 3days 做了 ybtoj 的 3 道例题，真是太有效率了！！1

为了避免自己没学明白就瞎写东西误人子弟，这篇 Blog 拖到了现在。
图片基本沿用 OIwiki，原文跳步骤（主要是 access 部分）的就自己补画了一些。
不过反正也没啥人看？

前置知识

Splay

欢迎阅读 Splay 详细图解 & 轻量级代码实现。
其实 LCT 对 Splay 的要求主要体现在维护序列的能力上，如果平时更习惯用其它平衡树，单纯为了学 LCT 去学 Splay 的话，“应用”那一段都不用看，会 rotate & splay & reverse 以及维护一些简单的序列操作（区间加区间乘？）就足够了。
据说无旋 Treap 也能用来维护 LCT，但复杂度多一个 $\log$，不建议大家这么写。不过如果真的痛恨 Splay 也可以去学学：Link

下文 Splay（大写）表示树，splay（小写）表示操作。

树链剖分

没写过博客，但应该没人学 LCT 不会这个吧。

动态树

动态树，顾名思义就是维护一个森林，支持连边和删边操作，要求维护树上的一些特定信息。
LCT(link cut tree)，是一种解决动态树问题的数据结构。LCT 不叫动态树。

实链剖分

基于上文对动态树问题的概述，我们以 lg P3690 【模板】动态树（LCT） 为例看看 lct 具体用来干什么。

假设有这样的问题。

给一棵树，要求支持如下操作：

• 修改一个点的点权
• 查询路径 $x$ 到 $y$ 的点权异或和

不难想到，这个问题容易使用重链剖分在 $O(n\log n)$ 的时间复杂度内解决。

但如果这个森林是动态的，即改成支持如下操作：

• 修改一个点的点权
• 断开 $x$ 和 $y$ 之间的连边
• 在 $x$ 和 $y$ 之间连一条边，保证连边后还是一个森林
• 查询路径 $x$ 到 $y$ 的点权异或和

朴素的静态树链剖分难以维护这个问题，因为我们在改变树的结构时，树链剖分的形态也应随之改变。我们需要换一种方法来解决问题。

考虑重链剖分维护链上操作的本质，是给同一条链上的点赋上相邻的 $dfn$ 编号，并保证从叶子到根经过的链的条数为 $\log$ 级别，从而方便使用其他数据结构维护。
而在动态树中，问题的瓶颈变成了怎么让树链的划分状况随树的形态快速修改。考虑沿用重链剖分的思路，发现 $size$ 是难以维护的；那我们显然更希望每个点的轻重儿子是我们自己指定的，而不是遵守特定的规则，这样在改变树形态的时候可以更自由地维护树链的变化。

我们把这种“自己指定轻重儿子”的剖分方式成为实链剖分，同一条链里的点之间连的边叫做实边，不同链之间的边叫虚边。其中每个点用实边相连的儿子叫实儿子，其余的叫虚儿子。

虽然这样划分是很自由的，但要注意它和树剖的区别：

• 每个非叶子节点至多有一个实儿子，但也可以一个都没有；
• 由上条可知，一条实链不一定要一直延伸到叶子节点。

现在，这棵树被我们划分成了若干实链。考虑使用 Splay 来分别维护这些链。对于一个链上的整体操作，我们就通过对这棵 Splay 维护区间操作来实现。

辅助树

在学习 LCT 的操作之前，要先了解辅助树的定义及其结构。

辅助树，就是维护每个树链的 Splay 之间通过某种方式相连接形成的树形结构。可以认为，Splay 维护的是一条实链，辅助树维护的是一棵树；一些辅助树放在一起就形成了 LCT，LCT 维护的是整个森林。
它满足如下性质：

• 辅助树由多棵 Splay 构成，其中每棵 Splay 维护的是原树的一条实链，且这棵 Splay 的中序遍历一一对应实链从上到下的点；
• 原树的每个点和辅助树上的点一一对应；
• 辅助树上的 Splay 之间通过某种方式连接成树形结构。具体地，我们原来学习的 Splay 根节点为空，但辅助树上的 Splay 不同，维护每条实链的 Splay，它根节点的父亲指向 这条实链顶端的点的父亲。注意不是指向 Splay 根节点在原树上的父亲。同时，对于根节点的父亲，它的两个儿子均不指向该点，这表示这条边是虚边。也就是说，所有实边是双向连接的；而虚边认父不认子，只能从儿子找父亲，父亲找不到儿子。我们可以根据这点来判断哪些点是 Splay 的根节点。
• 根据以上性质，我们在原树上所要进行的操作都可以在辅助树上进行，故下文的操作若无特别说明，均基于辅助树。

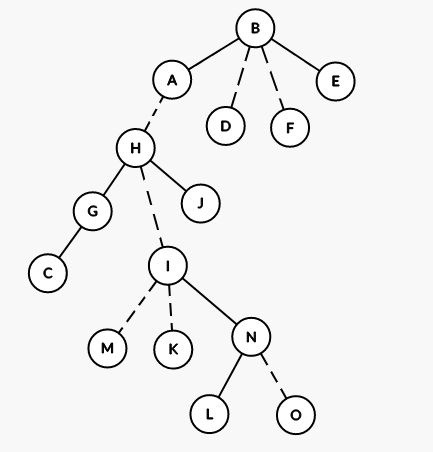
举个例子，一棵长成这样的树（实线为实边，虚线为虚边）：

它的一种辅助树就可以长成这样（不认为这张图很难理解，所以直接贺过来了）：

学习 Splay 时，我们记得同一个序列能构成的 Splay 有很多种不同形态，LCT 是同理的，对于相同的树形态和虚实边划分，由于 Splay 形态的不同，可以有很多种形态不同的辅助树。

那么我们得到了辅助树和原树之间的关系：

• 原树的实链都在辅助树的同一个 Splay 中；实边在 Splay 里中序遍历相邻，但不一定直接有边相连。
• 原树的虚边，由儿子所在 Splay 的根节点指向该点，但该点不指向虚儿子。
• Splay 上虽然至多只有两个实儿子，但剩下多出来的都是虚边，虚边可以有很多条。
• 原树的根不等于辅助树的根，辅助树在不破坏 Splay 性质的情况下可以随意换根。
• 原树的 father 指向和辅助树不同，注意区分。
• 在辅助树上，更易于进行虚实链之间的变换，这一点会在后文进行讲解。

常用函数的实现 - Splay 原有函数

知道了实链剖分和辅助树的概念，就可以开始实现 LCT 的一些常用函数了 qwq。
LCT 里使用的 Splay，由于根节点父亲不为空的定义与普通 Splay 不同，在写法上也需要做出一些改动。

我们先从简单的开始：

get

判断 $x$ 是它父亲的哪个儿子。在 Splay 里面学习过了，不用改动。

il bool get(int x) {return rs(fa(x))==x;}

isroot

LCT 独有的函数，判断 $x$ 是否为这棵 Splay 的根。
根据虚边认父不认子的性质，如果 $x$ 父亲的两个儿子都找不到它，这条连边就是虚边，即 $x$ 是 Splay 的根。

il bool isroot(int x) {return ls(fa(x))!=x&&rs(fa(x))!=x;}

pushup

在儿子节点改变时上传信息。以上文所述的题意为例，我们需要在 pushup 中更新这棵 Splay 的异或和。

il void pushup(int x) 
{
    // pushup other things here
    tr[x].sum=tr[x].key^tr[ls(x)].sum^tr[rs(x)].sum;
}

pushdown

下传标记。
LCT 绝大部分时候都要在 Splay 上维护区间翻转标记，原因后文会讲。同时，根据题里的要求打的其他标记（这道题没有）也要一起下传。
这里和文艺平衡树一样，翻转标记有两种不同含义的写法：

• 一种是打标记的时候，这个点左右儿子已经换过了，标记表示它的两个儿子要换左右儿子；
• 另外一种是打标记表示这个点要换左右儿子，但现在还没换。

两种写法没有什么本质区别，但在后面一些地方 pushdown 的顺序写起来不一样。后文遇到有区别的地方会提到。
另外有些题，点 $x$ 维护的信息与左右儿子的顺序有关。这个时候第二种就是错的，只能用第一种写法。 后文有相关例题。
这里为了代码简单，写的是第二种。

il void pushdown(int x)
{
    // pushdown other tags here
    if(!tr[x].lz) return;
    swap(ls(x),rs(x)),tr[ls(x)].lz^=1,tr[rs(x)].lz^=1;
    tr[x].lz=0;
}

update

update(x) 表示从 $x$ 所在 Splay 的根开始，沿从根到 $x$ 的链一路下放标记。
用于在 Splay(x) 前，保证 $x$ 旋转时一路要经过的点的左右儿子都是正确的。
递归下放即可。

（upd: 文艺平衡树不需要这种东西是因为用来找对应排名节点的 $\text{find}$ 操作把标记都下放了，但是 lct 不关心排名没有这个函数。）

il void update(int x)
{
    if(!isroot(x)) update(fa(x));
    pushdown(x);
}

rotate

与原义相同，把 $x$ 向上旋转一层。
写法上和在 Splay 中学习的略有区别，因为我们要判断 $y$ 是否是根，不能再简单地根据 $z$ 的值是否为 $0$ 来判断。
而把 $y$ 和父亲的连边断开再判断会造成 isroot(y) 失效，所以我们把这句话提到前面：

il void rotate(int x)
{
    int y=fa(x),z=fa(y),c=get(x);
    if(!isroot(y)) tr[z].s[get(y)]=x; // here
    fa(tr[x].s[c^1])=y,tr[y].s[c]=tr[x].s[c^1],tr[x].s[c^1]=y;
    fa(y)=x,fa(x)=z; pushup(y),pushup(x);
}

Splay

把判断是否为根的语句换成 isroot 即可。注意 Splay 之前要先 update 这条路径，防止出现左右儿子顺序不对/未下传的标记跑到别的节点上的情况。
LCT 不需要形如把 $x$ 转到某个点儿子的 Splay 函数，因为区间操作都是对整棵树操作。

il void splay(int x)
{
    update(x);
    for(int f=fa(x);f=fa(x),!isroot(x);rotate(x))
        if(!isroot(f)) rotate(get(f)==get(x)?f:x);
}

常用函数的实现 - LCT 的新函数

Splay 中出现过的基本函数到这里就讲完了，已经承包了 LCT 的绝大部分码量！
下文将对 LCT 特有的函数逐一讲解，或许不再像上文那么容易理解，但代码都非常简短（确信。

access

access(x) 的作用是把 $x$ 到原树的根这条路径上的边都变成实链，同时其他原来与这条路径相连的实边都变成虚边。
换句话讲，把 $x$ 到根的路径放到同一棵 Splay 里，而且这棵 Splay 里没有这条路径以外的点。
这是 lct 最基本的函数，写任何 lct 都必须要实现 access 操作。

注意要时刻分清楚原树的根和辅助树的根。
后面读到哪里发现读不懂就往上翻翻加粗的字，看看是不是什么地方混淆了概念 >_<（樱雪喵学的时候一直反反复复把概念搞混，所以看了一天才看懂（哭）

下面图比较多，为了避免来回翻页的痛苦把图缩小了（但貌似还是要来回翻页）。看不清可以单击放大，不过应该不至于（
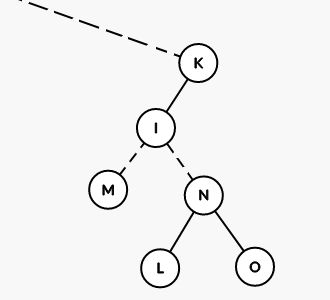
还是以一开始举例子那张图为例，原树长这样：

辅助树长这样：

现在执行 access(N)，我们希望它的原树变成这样：

当然辅助树会变成什么样我们还想象不出来，不过不急。

一步一步来。
我们要 access(N)，那先把辅助树上的 $N$ Splay 到根吧：

然后发现，要的是从 $N$ 到原树的根的这条链，但是我们不想要 $N$ 在原树上的儿子。原来的虚儿子当然不用管；只要把原来 $N$ 的实儿子变成虚儿子就好了。

考虑原来 $N$ 的实儿子在什么地方。根据 Splay 的性质，它的中序遍历是这个实链从上到下的点的顺序。那 $N$ 在原树上的实儿子就是在现在的 Splay 上根节点的后继。
当然不用麻烦地去找后继在哪里，因为凡是 $N$ 下面的链上的我们都不要。那直接把 $N$ 的右儿子和 $N$ 断开，改成虚边就可以了。
根据虚边认父不认子的性质，我们单方面地把 rs(N) 置为 $0$。

现在这条边变成了虚边：

接下来，我们已经根据 $N$ 在辅助树上的的父亲，知道了链头在原树上的父亲是 $I$。也就是说我们想把 $L\to N$ 这条链 接在 $I$ 下面。
同样把 $I$ splay 到根。这里 splay 的时候不会改变虚儿子指向 $I$ 的虚边，一定要理解哪些边会跟着点的旋转跑，哪些不会（比如根的父亲这条边）。

现在我们希望 $N$ 这棵树接在 $I$ 下面，即 $I$ 在 Splay 上的右儿子；但是 $I$ 在 Splay 上已经有右儿子了，这意味着现在的 $I$ 有实儿子。那么我们要把这个点 $K$ 变成虚儿子，然后把 $N$ 所在的这条链变成实儿子。
同样地，单方面令 rs(I)=N 即可。

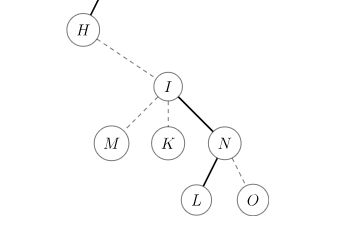
现在 $I\to L\to N$ 在一个实链里了。同理，我们按照上面的步骤继续。
因为 $I$ 的父亲是 $H$，代表这条实链顶端的父亲是 $H$。所以我们把 $H$ Splay 到根：

然后把 $H$ 的右儿子换成 $I$：

继续 Splay(A) 并令 rs(A)=H，相信大家能画明白怎么转，这里不分步了。

发现现在原树上 $A\to C\to G\to H\to I\to L\to N$ 这条链正好在一棵 Splay 里了。
我们再回顾一下刚刚是怎么转的：

• 把当前节点 splay 到根；
• 令它的右儿子等于上次旋转的节点，并 pushup；
• 跳到当前点的父亲，重复以上步骤。

说了这么多，代码就一行，$p$ 表示上次转的点。

il void access(int x) {for(int p=0;x;p=x,x=fa(x)) splay(x),rs(x)=p,pushup(x);}

makeroot

另一个重要的 lct 函数，写绝大部分题时都需要实现。不过确实有例外，比如 lg P4332 [SHOI2014] 三叉神经树 这种保证深度递增的题就不用写。
在维护一个路径信息时，往往不能保证路径深度递增，很多时候路径是先向上再向下的。根据辅助树的性质，这样的路径无法出现在同一棵 Splay 里。
但是我们还想维护它的信息，怎么办呢。
可以把原树的根换掉啊。makeroot(x) 的作用就是把 $x$ 换成原树的根。
但是 Splay 里的点是按中序遍历从上到下存的，设原来的原树根是 $rt$，考虑换成 $x$ 会对哪些点的上下顺序产生影响：
只有 $x$ 到 $rt$ 这条路径上的点上下顺序反过来了，剩下的都没变。上下顺序反过来，貌似就是把这一段的 Splay 区间翻转？
那我们先 access(x)，把 $x$ 到 $rt$ 弄到一棵 Splay 上。但你发现你不知道 access 完 Splay 的根是啥。所以 splay(x) 让 $x$ 变成根你就知道了。最后在这个点上打 lazytag。

这就是为什么在 pushdown 里说 lct 的 splay 一般都要维护区间翻转标记。

il void makeroot(int x) {access(x),splay(x),tr[x].lz^=1;}

find

find(x) 的作用是查找 $x$ 所在原树的根。
我们知道，access(x) 也是把 $x$ 到原树的根这一段变成实链。那么先 access(x)，再 splay(x)，以 $x$ 为根的这个 Splay 就表示从原树的根到 $x$ 的实链。
根据 Splay 的性质，原树的根是这条链从上到下第一个点，也就是这棵 Splay 中序遍历里的第一个点。
Splay 中序遍历里的第一个点，不难发现就是 $x$ 一直往左儿子走，直到没有左儿子，这个点就是原树的根。

注意我们打的 lazytag 表示还没有交换这个点的两个儿子，所以对每个点要先 pushdown 再判断有没有左儿子。
同理，如果你采用了 lazytag 的另一种定义，就把这个 pushdown 放到后面，因为这个点本身已经换过了。

找到根后要 splay(x) 来保证复杂度。（hack 形如 Splay 那篇文章的 rank 部分，一直查同一个很深的点）

il int find(int x)
{
    access(x),splay(x);
    while(pushdown(x),ls(x)) x=ls(x);
    return splay(x),x;
}

split

split(x,y) 的作用是把 $x$ 到 $y$ 的路径拿出来变成一棵 Splay。
我们需要保证这条路径深度递增，所以先令 $x$ 成为原树的根：makeroot(x);
接下来执行 access(y)，就找到了这条路径。还有个问题是这样不知道 Splay 的根，所以后面一般会再做一步 splay(y)。

il void split(int x,int y) {makeroot(x),access(y),splay(y);}

link

link(x,y) 表示在森林里给 $x$ 和 $y$ 之间连一条边。
那么我们先 makeroot(x)，让 $x$ 成为自己这棵树的根（原树、辅助树都是），然后判断它们两个是否已经连通。
如果不连通，直接把点 $x$ 作为虚儿子单向指向 $y$ 即可。

il void link(int x,int y) {makeroot(x);if(find(y)!=x) fa(x)=y;}

cut

cut(x,y) 表示删除森林中 $x$ 到 $y$ 的边。
我们同样先 makeroot(x)。
这里要判断操作是否合法，当然可以用 map 一类的东西记录，但也可以从 Splay 结构的角度考虑。$x$ 到 $y$ 有边，当且仅当：

• $x$ 和 $y$ 连通；
• $x$ 到 $y$ 的路径之间没有其他点；

前者可以用 find(y)==x 判断。对于后者，$y$ 和 $x$ 直接相连，当且仅当 $y$ 是 $x$ 的右儿子，并且 $y$ 没有左儿子。
你可能会奇怪，既然反正也要判后面这一半，前面还判 find(y)==x 干什么？
这里的 find(y) 里面同时隐含了 access(y) 和 splay(x) 的操作，是为了保证这两个点之间是实边、$x$ 是 Splay 的根的。
当然你手动拆出来写这两句话也行！

确定了 $x$ 和 $y$ 确实有边之后，我们令 fa(y)=rs(x)=0，将它们双向断开。

il void cut(int x,int y)
{
    makeroot(x);
    if(find(y)==x&&fa(y)==x&&!ls(y)) fa(y)=rs(x)=0;
}

注意到这里的 pushup(x) 可以不写。看起来似乎不太符合常理，但仔细思考一下发现是对的：
考虑不 pushup 会对什么地方造成影响。因为 $x$ 一定是 Splay 的根节点，所以它不 pushup 只会造成它自己的值不对。我们考虑接下来的操作。

• 如果是查询（split），那会对根节点进行 access 操作，access 里面有 pushup；
• 如果是修改树的形态，$x$ 被 rotate 下去的时候也会被 pushup。

那么我们成功证明了这么做的正确性。

时间复杂度证明

记住是 $O(n\log n)$ 就行，如果想研究怎么证明的话可以看 Link。

完整代码 & 一些建议

所有 LCT 的基本操作到这里就讲完了。这里给出一个 lg P3690 【模板】动态树（LCT） 的代码。
可以看出来比 Splay 板子短好多。

点击查看代码

#include
#define il inline
using namespace std;
il int read()
{
    int xr=0,F=1; char cr;
    while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
    while(cr>='0'&&cr<='9') 
        xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
    return xr*F;
}
const int N=3e5+5;
struct node
{
    int key,sum,fa,lz;
    int s[2];
    node() {key=sum=fa=lz=s[0]=s[1]=0;}
}tr[N];
#define ls(x) tr[(x)].s[0]
#define rs(x) tr[(x)].s[1]
#define fa(x) tr[(x)].fa
il bool get(int x) {return rs(fa(x))==x;}
il bool isroot(int x) {return ls(fa(x))!=x&&rs(fa(x))!=x;}
il void pushup(int x) {tr[x].sum=tr[ls(x)].sum^tr[rs(x)].sum^tr[x].key;}
il void pushdown(int x)
{
    if(!tr[x].lz) return;
    swap(ls(x),rs(x)),tr[ls(x)].lz^=1,tr[rs(x)].lz^=1;
    tr[x].lz=0;
}
il void update(int x)
{
    if(!isroot(x)) update(fa(x));
    pushdown(x);
}
il void rotate(int x)
{
    int y=fa(x),z=fa(y),c=get(x);
    if(!isroot(y)) tr[z].s[get(y)]=x;
    fa(tr[x].s[c^1])=y,tr[y].s[c]=tr[x].s[c^1],tr[x].s[c^1]=y;
    fa(y)=x,fa(x)=z; pushup(y),pushup(x);
}
il void splay(int x)
{
    update(x);
    for(int f=fa(x);f=fa(x),!isroot(x);rotate(x))
        if(!isroot(f)) rotate(get(f)==get(x)?f:x);
}
il void access(int x) {for(int p=0;x;p=x,x=fa(x)) splay(x),rs(x)=p,pushup(x);}
il void makeroot(int x) {access(x),splay(x),tr[x].lz^=1;}
il int find(int x)
{
    access(x),splay(x);
    while(pushdown(x),ls(x)) x=ls(x);
    return splay(x),x;
}
il void link(int x,int y) {makeroot(x);if(find(y)!=x) fa(x)=y;}
il void split(int x,int y) {makeroot(x),access(y),splay(y);}
il void cut(int x,int y)
{
    makeroot(x);
    if(find(y)==x&&fa(y)==x&&!ls(y)) fa(y)=rs(x)=0;
}
int main()
{
    int n=read(),m=read();
    for(int i=1;i<=n;i++) tr[i].key=read();
    while(m--)
    {
        int op=read(),x=read(),y=read();
        if(op==0) split(x,y),printf("%d\n",tr[y].sum);
        if(op==1) link(x,y);
        if(op==2) cut(x,y);
        if(op==3) makeroot(x),splay(x),tr[x].key=y;
    }
    return 0;
}

说一点本喵调了几天 LCT 获得的经验。
基本的板子一定要记熟。就算一开始记不住可以对着原来的看，但打个几遍总该差不多背下来。
理解原理然后不特地去背，自己就能写出来当然是很神仙的；但是写挂了调起来确实麻烦（某天手画了一整张纸的 splay 试图找哪里有锅，最后是 rotate 写错了）。

或许这个笨办法只适用于没有脑子的樱雪喵？

LCT 的各种应用

维护树链信息

比较板的应用。一般来说就是在动态树上维护某些树链之间的信息，比如区间和之类的东西。
LCT 的写法在下面三个例题里都是完全一致的，区别只有 pushup pushdown 以及 Splay 维护的东西不同。

P3690 【模板】动态树（LCT）

题意：动态树，支持加边删边，单点修改，查询路径上的点权异或和。

上文说过的板子题，代码见上文。

P1501 [国家集训队] Tree II

题意：支持加边删边，对一条路径区间加 / 区间乘，查询路径点权和。

对一条路径进行区间加 / 区间乘，可以仿照 【模板】线段树 2 的方法，给 Splay 的节点分别打加法和乘法标记。
但是 Splay 和线段树不一样的地方在于子树 $size$ 不固定，所以也要单独维护；且 Splay 的区间是 左子树+自己+右子树，线段树少自己这一项，在 pushup 的时候要根据这点适当改动。
坑点是模数看起来很小，但平方会爆 int。

点击查看代码

#include
#define il inline
using namespace std;
il int read()
{
    int xr=0,F=1; char cr;
    while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
    while(cr>='0'&&cr<='9') 
        xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
    return xr*F;
}
#define int long long
const int N=1e5+5,mod=51061;
struct node
{
    int siz,lz,sum,key,addtag,multag;
    int s[2],fa;
    node() {siz=lz=sum=key=addtag=s[0]=s[1]=fa=0;multag=1;}
}tr[N];
#define ls(x) tr[(x)].s[0]
#define rs(x) tr[(x)].s[1]
#define fa(x) tr[(x)].fa
il bool get(int x) {return x==rs(fa(x));}
il bool isroot(int x) {return ls(fa(x))!=x&&rs(fa(x))!=x;}
il void pushup(int x)
{
    tr[x].siz=tr[ls(x)].siz+tr[rs(x)].siz+1;
    tr[x].sum=(tr[ls(x)].sum+tr[rs(x)].sum+tr[x].key)%mod;
}
il void pushdown(int x)
{
    if(tr[x].lz)
    {
        swap(ls(ls(x)),rs(ls(x))),swap(ls(rs(x)),rs(rs(x)));
        tr[ls(x)].lz^=1,tr[rs(x)].lz^=1;
        tr[x].lz=0;
    }
    int mult=tr[x].multag,addt=tr[x].addtag;
    (tr[ls(x)].sum*=mult)%=mod,(tr[ls(x)].key*=mult)%=mod;
    (tr[rs(x)].sum*=mult)%=mod,(tr[rs(x)].key*=mult)%=mod;
    (tr[ls(x)].addtag*=mult)%=mod,(tr[ls(x)].multag*=mult)%=mod;
    (tr[rs(x)].addtag*=mult)%=mod,(tr[rs(x)].multag*=mult)%=mod;
    tr[x].multag=1;
    (tr[ls(x)].sum+=addt*tr[ls(x)].siz)%=mod,(tr[ls(x)].key+=addt)%=mod;
    (tr[rs(x)].sum+=addt*tr[rs(x)].siz)%=mod,(tr[rs(x)].key+=addt)%=mod;
    (tr[ls(x)].addtag+=addt)%=mod,(tr[rs(x)].addtag+=addt)%=mod;
    tr[x].addtag=0;
}
il void update(int x)
{
    if(!isroot(x)) update(fa(x));
    pushdown(x);
}
il void rotate(int x)
{
    int y=fa(x),z=fa(y),c=get(x);
    if(!isroot(y)) tr[z].s[get(y)]=x;
    fa(tr[x].s[c^1])=y,tr[y].s[c]=tr[x].s[c^1],fa(y)=x,tr[x].s[c^1]=y;
    fa(x)=z; pushup(y),pushup(x);
}
il void splay(int x)
{
    update(x);
    for(int f=fa(x);f=fa(x),!isroot(x);rotate(x))
        if(!isroot(f)) rotate(get(f)==get(x)?f:x);
}
il void access(int x) {for(int p=0;x;p=x,x=fa(x)) splay(x),rs(x)=p,pushup(x);}
il void makeroot(int x) {access(x),splay(x);swap(ls(x),rs(x)),tr[x].lz^=1;}
il void split(int x,int y) {makeroot(x),access(y),splay(y);}
il int find(int x)
{
    access(x),splay(x);
    while(ls(x)) x=ls(x),pushdown(x);
    return splay(x),x;
}
il void link(int x,int y) {makeroot(x);if(find(y)!=x) fa(x)=y,pushup(y);}
il void cut(int x,int y)
{
    makeroot(x);
    if(find(y)==x&&fa(y)==x&&!ls(y)) rs(x)=fa(y)=0,pushup(x);
}
signed main()
{
    int n=read(),q=read();
    for(int i=1;i<=n;i++) tr[i].key=1;
    for(int i=1;i>c;
        if(c=='+')
        {
            int x=read(),y=read(),c=read();
            split(x,y),(tr[y].key+=c)%=mod,(tr[y].sum+=c*tr[y].siz)%=mod;
            (tr[y].addtag+=c)%=mod;
        }
        if(c=='-')
        {
            int u=read(),v=read(),x=read(),y=read();
            cut(u,v),link(x,y);
        }
        if(c=='*')
        {
            int x=read(),y=read(),c=read();
            split(x,y);
            (tr[y].key*=c)%=mod,(tr[y].sum*=c)%=mod;
            (tr[y].multag*=c)%=mod,(tr[y].addtag*=c)%=mod;
        }
        if(c=='/')
        {
            int x=read(),y=read();
            split(x,y);
            printf("%lld\n",tr[y].sum);
        }
    }
    return 0;
}

P4842 城市旅行

题意：动态树，支持对一条路径区间加，求在一条给定路径上随机选两个点，这两个点之间路径点权和的期望。

如果你觉得上一道题 Splay 打标记打得不够过瘾，可以写写这个题。
期望是个幌子，实际就是让你维护这条路径的每条子路径的点权和的和。考虑路径上第 $x$ 个点的贡献，设路径长度为 $n$，那么它的贡献是 $a_x\times (x)(n-x+1)$。
然后用 Splay 维护这个东西。具体柿子不推了，可以去看题解。
总之最后要维护 $siz,rev,addtag,key,res,sum,suml,sumr$。祝你能调出来（。

Warning. 这个题就属于之前说的“维护的信息与左右儿子的顺序有关”的一类，翻转标记只能用第一种写法。下放翻转标记的时候别忘了把 $suml$ 和 $sumr$ 也一起颠倒过来。

点击查看代码 ``` 不知道触发了什么神秘特性，这段代码一粘进去博客就崩。 只能放提交记录了。 https://www.luogu.com.cn/record/124594260 ```

P4332 [SHOI2014] 三叉神经树

题意：给一棵树，每个点有三个儿子。除叶子节点的黑白已给定外，每个点的颜色是儿子中较多的那一种颜色。修改叶子节点，问根节点颜色。

和上面三个题不太一样，这道题里的 Splay 维护的是最深的恰有 1/2 个儿子为黑色的节点编号。
是比较罕见的不用写 makeroot 和 reverse 的 lct。

点击查看代码

#include
#define il inline
using namespace std;
il int read()
{
    int xr=0,F=1; char cr;
    while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
    while(cr>='0'&&cr<='9') 
        xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
    return xr*F;
}
const int N=1.5e6+5;
struct node
{
    int sum,lz,res1,res2;
    int s[2],fa;
    node() {sum=fa=lz=res1=res2=s[0]=s[1]=0;}
}tr[N];
#define ls(x) tr[(x)].s[0]
#define rs(x) tr[(x)].s[1]
#define fa(x) tr[(x)].fa
il bool get(int x) {return x==rs(fa(x));}
il bool isroot(int x) {return x!=ls(fa(x))&&x!=rs(fa(x));}
il void pushup(int x)
{
    tr[x].res1=tr[rs(x)].res1,tr[x].res2=tr[rs(x)].res2;
    if(!tr[x].res1)
    {
        if(tr[x].sum!=1) tr[x].res1=x;
        else tr[x].res1=tr[ls(x)].res1;
    }
    if(!tr[x].res2)
    {
        if(tr[x].sum!=2) tr[x].res2=x;
        else tr[x].res2=tr[ls(x)].res2;
    }
}
il void pushdown(int x)
{
    if(!tr[x].lz) return;
    tr[ls(x)].sum+=tr[x].lz,tr[rs(x)].sum+=tr[x].lz;
    swap(tr[ls(x)].res1,tr[ls(x)].res2);
    swap(tr[rs(x)].res1,tr[rs(x)].res2);
    tr[ls(x)].lz+=tr[x].lz,tr[rs(x)].lz+=tr[x].lz;
    tr[x].lz=0;
}
il void update(int x)
{
    if(!isroot(x)) update(fa(x));
    pushdown(x);
}
il void rotate(int x)
{
    int y=fa(x),z=fa(y),c=get(x);
    if(!isroot(y)) tr[z].s[get(y)]=x;
    fa(tr[x].s[c^1])=y,tr[y].s[c]=tr[x].s[c^1],fa(y)=x,tr[x].s[c^1]=y;
    fa(x)=z; pushup(y),pushup(x);
}
il void splay(int x)
{
    update(x);
    for(int f=fa(x);f=fa(x),!isroot(x);rotate(x))
        if(!isroot(f)) rotate(get(f)==get(x)?f:x);
}
il void access(int x) {for(int p=0;x;p=x,x=fa(x)) splay(x),rs(x)=p,pushup(x);}

int n;
vector E[N];
void dfs(int u)
{
    for(auto v:E[u]) dfs(v),tr[u].sum+=(tr[v].sum>1);
}
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=3;j++)
        {
            int x=read();
            E[i].push_back(x),tr[x].fa=i;
        }
    }
    for(int i=n+1;i<=3*n+1;i++) tr[i].sum=read()+1;
    dfs(1);
    // cout<1
        {
            access(f),splay(f);
            if(tr[f].res1)
            {
                int now=tr[f].res1;
                splay(now);
                tr[now].sum++,tr[rs(now)].sum++,tr[rs(now)].lz++;
                swap(tr[rs(now)].res1,tr[rs(now)].res2),pushup(now);
            }
            else tr[f].sum++,tr[f].lz++,swap(tr[f].res1,tr[f].res2);
        }
        else
        {
            access(f),splay(f);
            if(tr[f].res2)
            {
                int now=tr[f].res2;
                splay(now);
                tr[now].sum--,tr[rs(now)].sum--,tr[rs(now)].lz--;
                swap(tr[rs(now)].res1,tr[rs(now)].res2),pushup(now);
            }
            else tr[f].sum--,tr[f].lz--,swap(tr[f].res1,tr[f].res2);
        }
        tr[x].sum=(tr[x].sum==1)?2:1,splay(1);
        printf("%d\n",tr[1].sum>1?1:0);
    }
    return 0;
}

维护连通性

lg P2147 [SDOI2008] 洞穴勘测

给一堆点，支持加边删边，保证始终是森林，询问两点是否连通。

之前写 link 的时候就用到过判断连通，先 makeroot 再 find 就可以了。
这里应当有一些别的题，但是先摆。

点击查看代码

#include
#define il inline 
using namespace std;
il int read()
{
	int xr=0,F=1; char cr=getchar();
	while(cr<'0'||cr>'9') {if(cr=='-') F=-1;cr=getchar();}
	while(cr>='0'&&cr<='9') 
		xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
	return xr*F;
}
const int N=2e5+5;
#define ls(x) tr[(x)].s[0]
#define rs(x) tr[(x)].s[1] 
struct tree{
	int fa,lz,s[2];
}tr[N];
int n,m;
void push_down(int x)
{
	if(!tr[x].lz) return;
	swap(ls(ls(x)),rs(ls(x))),swap(ls(rs(x)),rs(rs(x)));
	tr[ls(x)].lz^=1,tr[rs(x)].lz^=1;
	tr[x].lz=0;
}
bool get(int x) {return x==tr[tr[x].fa].s[1];}
bool isroot(int x) {return ls(tr[x].fa)!=x&&rs(tr[x].fa)!=x;}
void rotate(int x)
{
	int y=tr[x].fa,z=tr[y].fa,chk=get(x);
	if(!isroot(y)) tr[z].s[get(y)]=x;
	if(tr[x].s[chk^1]) tr[tr[x].s[chk^1]].fa=y;
	tr[y].s[chk]=tr[x].s[chk^1];tr[x].s[chk^1]=y,tr[y].fa=x;
	tr[x].fa=z;
}
void update(int x)
{
	if(!isroot(x)) update(tr[x].fa);
	push_down(x);
}
void splay(int x)
{
	update(x);
	for(int f=tr[x].fa;f=tr[x].fa,!isroot(x);rotate(x)) 
		if(!isroot(f)) rotate(get(f)==get(x)?f:x);
}
void access(int x) {for(int p=0;x;p=x,x=tr[x].fa) splay(x),rs(x)=p;}
void make_root(int x) {access(x),splay(x);swap(ls(x),rs(x)),tr[x].lz^=1;}
int find(int x)
{
	access(x),splay(x);
	while(ls(x)) push_down(x),x=ls(x);
	splay(x);return x;
}
void link(int x,int y) {make_root(x);if(find(y)!=x) tr[x].fa=y;}
void cut(int x,int y)
{
	make_root(x);
	if(find(y)==x&&tr[y].fa==x&&(!ls(y))) tr[y].fa=rs(x)=0;
}
int main()
{
	n=read(),m=read();
	while(m--)
	{
		string s;cin>>s;
		int x=read(),y=read();
		if(s=="Query")
		{
			if(find(x)==find(y)) printf("Yes\n");
			else printf("No\n");
		}
		else if(s=="Connect") link(x,y);
		else cut(x,y);
	}
	return 0;
}

维护生成树

对于维护边权相关的问题，我们发现由于 LCT 的灵活性很高，同时辅助树上的边也与原树的边不相同，因此无法简单地通过点权来定位一条边的边权。
解决方法是，我们新建一些点，令每个点代表一条边，边权记在对应点的点权上。那么每次连边删边时，我们分别 link 和 cut 两次，把边的两个端点和代表边权的点分别连接 / 断开。

P4234 最小差值生成树

题意：给 $n$ 个点 $m$ 条边的图，求最大最小边权之差最小的生成树。

考虑从小到大加入边，并维护当前情况下最小边权的最大值。

• 如果当前 $u,v$ 已经连通，那么在 $u,v$ 的路径上找到边权最小的边，并把它删掉，改为加入当前的新边；
• 如果当前 $u,v$ 不连通，直接加入这条边。

对于一条路径上边权最小的边，转为点权后就是一棵 Splay 里点权最小的点。所以只需在 Splay 里维护点权最小的编号。

点击查看代码

#include
#define il inline
using namespace std;
il int read()
{
    int xr=0,F=1; char cr;
    while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
    while(cr>='0'&&cr<='9') 
        xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
    return xr*F;
}
const int N=3e5+5,inf=1e9;
struct node
{
    int key,id,lz;
    int s[2],fa;
}tr[N];
#define ls(x) tr[(x)].s[0]
#define rs(x) tr[(x)].s[1]
#define fa(x) tr[(x)].fa
il bool get(int x) {return x==rs(fa(x));}
il bool isroot(int x) {return x!=ls(fa(x))&&x!=rs(fa(x));}
il void pushup(int x)
{
    tr[x].id=x,tr[0].id=0,tr[0].key=inf;
    if(tr[tr[ls(x)].id].key

P2387 [NOI2014] 魔法森林

和上一题本质相同，但是这里可能会出现路径上已有的最大边比当前边小的情况，注意判断。
很不理解为什么 ybtoj 要把这玩意放在板子后面的第一道例题，我第一次对着 ybtoj 学 lct 就是被这东西劝退的 >_<

点击查看代码

#include
#define il inline
using namespace std;
il int read()
{
    int xr=0,F=1; char cr;
    while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
    while(cr>='0'&&cr<='9') 
        xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
    return xr*F;
}
const int N=1.5e5+5,inf=1e9;
struct node
{
    int id,key,lz;
    int s[2],fa;
}tr[N];
#define ls(x) tr[(x)].s[0]
#define rs(x) tr[(x)].s[1]
#define fa(x) tr[(x)].fa
il bool get(int x) {return x==rs(fa(x));}
il bool isroot(int x) {return x!=ls(fa(x))&&x!=rs(fa(x));}
il void pushup(int x)
{
    tr[x].id=x;
    if(tr[tr[ls(x)].id].key>tr[tr[x].id].key) tr[x].id=tr[ls(x)].id;
    if(tr[tr[rs(x)].id].key>tr[tr[x].id].key) tr[x].id=tr[rs(x)].id;
}
il void pushdown(int x)
{
    if(!tr[x].lz) return;
    swap(ls(x),rs(x)),tr[ls(x)].lz^=1,tr[rs(x)].lz^=1;
    tr[x].lz=0;
}
il void update(int x)
{
    if(!isroot(x)) update(fa(x));
    pushdown(x);
}
il void rotate(int x)
{
    int y=fa(x),z=fa(y),c=get(x);
    if(!isroot(y)) tr[z].s[get(y)]=x;
    fa(tr[x].s[c^1])=y,tr[y].s[c]=tr[x].s[c^1],tr[x].s[c^1]=y;
    fa(y)=x,fa(x)=z; pushup(y),pushup(x);
}
il void splay(int x)
{
    update(x);
    for(int f=fa(x);f=fa(x),!isroot(x);rotate(x))
        if(!isroot(f)) rotate(get(f)==get(x)?f:x);
}
il void access(int x) {for(int p=0;x;p=x,x=fa(x)) splay(x),rs(x)=p,pushup(x);}
il void makeroot(int x) {access(x),splay(x);tr[x].lz^=1;}
il void split(int x,int y) {makeroot(x),access(y),splay(y);}
il int find(int x)
{
    access(x),splay(x);
    while(pushdown(x),ls(x)) x=ls(x);
    return splay(x),x;
}
il void link(int x,int y) {makeroot(x);if(find(y)!=x) fa(x)=y;}
il void cut(int x,int y)
{
    makeroot(x);
    if(find(y)==x&&fa(y)==x&&!ls(y)) rs(x)=fa(y)=0,pushup(x);
}

bool flag[N];
int n,m,ans=inf;
struct edge{int u,v,a,b;}e[N];
bool cmp(edge x,edge y)
{
    if(x.a==y.a) return x.b<y.b;
    else return x.a<y.a;
}
int main()
{
    n=read(),m=read();
    for(int i=1;i<=m;i++) e[i]={read(),read(),read(),read()};
    sort(e+1,e+m+1,cmp);
    for(int i=1;i<=m;i++) tr[i+n].key=e[i].b;
    for(int i=1;i<=m;i++)
    {
        int u=e[i].u,v=e[i].v;
        if(u==v) continue;
        if(find(u)!=find(v))
        {
            link(u,i+n),link(v,i+n);
        }
        else
        {
            split(u,v);
            int id=tr[v].id;
            if(e[id-n].b>=e[i].b)
            {
                cut(e[id-n].u,id),cut(e[id-n].v,id);
                link(e[i].u,i+n),link(e[i].v,i+n);
            }
        }
        if(find(1)==find(n)) 
        {
            split(1,n);
            int mx=e[tr[n].id-n].b;
            ans=min(ans,e[i].a+mx);
        }
    }
    if(ans==inf) printf("-1\n");
    else printf("%d\n",ans);
    return 0;
}

---

看起来耗时一天终于写完了，寒假只会贺题解的东西一年后才补，我好菜啊。
有问题就评论区指出吧（
完结撒花 >w<