数据结构之平衡二叉树

一、定义

平衡二叉树也叫自平衡二叉搜索树（Self-Balancing Binary Search Tree），所以其本质也是一颗二叉搜索树，不过为了限制左右子树的高度差，避免出现倾斜树等偏向于线性结构演化的情况，所以对二叉搜索树中每个节点的左右子树作了限制，左右子树的高度差称之为平衡因子，树中每个节点的平衡因子绝对值不大于 1，此时二叉搜索树称之为平衡二叉树。

自平衡是指，在对平衡二叉树执行插入或删除节点操作后，可能会导致树中某个节点的平衡因子绝对值超过 ，即平衡二叉树变得“不平衡”，为了恢复该节点左右子树的平衡，此时需要对节点执行旋转操作。

二、平衡二叉树不平衡的情形

把需要重新平衡的结点叫做α，由于任意两个结点最多只有两个儿子，因此高度不平衡时，α结点的两颗子树的高度相差2.容易看出，这种不平衡可能出现在下面4中情况中：

（1）对α的左儿子的左子树进行一次插入
（2）对α的左儿子的右子树进行一次插入
（3）对α的右儿子的左子树进行一次插入
（4）对α的右儿子的右子树进行一次插入

情形1和情形4是关于α的镜像对称，二情形2和情形3也是关于α的镜像对称，因此理论上看只有两种情况，但编程的角度看还是四种情形。

第一种情况是插入发生在“外边”的情形（左左或右右），该情况可以通过一次单旋转完成调整；第二种情况是插入发生在“内部”的情形（左右或右左），这种情况比较复杂，需要通过双旋转来调整。

三、AVL树插入时的失衡与调整

AVL树的四种插入节点方式：

假设一颗 AVL 树的某个节点为 A，有四种操作会使 A 的左右子树高度差大于 1，从而破坏了原有 AVL 树的平衡性。平衡二叉树插入节点的情况分为以下四种：

（1）左旋（RR）

所谓LL（左旋）就是向左旋转一次，下图所示为最简洁的左旋（插入3导致值为1的节点不平衡）：

然而更多时候根节点并不是只有一个子树，下图为复杂的LL（左旋，插入13导致值为4的节点不平衡）：

红色节点为插入后不平衡的节点，黄色部分为需要改变父节点的分支，左旋后，原红色节点的右孩子节点变成了根节点，红色节点变成了它的左孩子，而它原本的左孩子（黄色部分）不能丢，而此时红色节点的右孩子是空的，于是就把黄色部分放到了红色节点的右孩子的位置上。调整后该二叉树还是一棵二叉排序（搜索）树，因为黄色部分的值大于原来的根节点的值，而小于后来的根节点的值，调整后，黄色部分还是位于原来的根节点（红色节点）和后来的根节点之间。

LL（左旋）代码如下：

node *LeftRotate(node *root) {
	//左旋 
	node *temp=root->right; 
	root->right=temp->left;
	temp->left=root;
	return temp;
}

代码解析：返回的是左旋后的根节点，左旋后的根节点是原来根节点的右孩子，左旋后的根节点的左孩子需要嫁接到原来根节点的右孩子上，原来的根节点嫁接到左旋后根节点的左孩子上。temp对应上图中值为8的节点，root对应上图中值为4的节点。

（2）右旋（LL）

所谓RR（右旋）就是向右旋转一次，下图所示为最简洁的右旋（插入1导致值为3的节点不平衡）：

然而更多时候根节点并不是只有一个子树，下图为复杂的RR（右旋，插入1导致值为9的节点不平衡）：

红色节点为插入后不平衡的节点，黄色部分为需要改变父节点的分支，右旋后，原红色节点的左孩子节点变成了根节点，红色节点变成了它的右孩子，而它原本的右孩子（黄色部分）不能丢，而此时红色节点的左孩子是空的，于是就把黄色部分放到了红色节点的左孩子的位置上。调整后该二叉树还是一棵二叉排序（搜索）树，因为黄色部分的值小于原来的根节点的值，而大于后来的根节点的值，调整后，黄色部分还是位于后来的根节点和原来的根节点（红色节点）之间。

RR（右旋）代码如下：

node *RightRotate(node *root) {
	//右旋 
	node *temp=root->left; 
	root->left=temp->right;
	temp->right=root;
	return temp;
}

代码解析：返回的是右旋后的根节点，右旋后的根节点是原来根节点的左孩子，右旋后的根节点的右孩子需要嫁接到原来根节点的左孩子上，原来的根节点嫁接到右旋后根节点的右孩子上。temp对应上图中值为5的节点，root对应上图中值为9的节点。

（3）先左旋再右旋（LR）

所谓LR（先左旋再右旋）就是先将左子树左旋，再整体右旋，下图为最简洁的LR旋转（插入2导致值为3的节点不平衡）：

然而更多时候根节点并不是只有一个子树，下图为复杂的LR旋转（插入8导致值为9的节点不平衡）：

先将红色节点的左子树左旋，红色节点的左子树的根原本是值为4的节点，左旋后变为值为6的节点，原来的根节点变成了左旋后根节点的左孩子，左旋后根节点原本的左孩子（蓝色节点）变成了原来的根节点的右孩子；再整体右旋，原来的根节点（红色节点）变成了右旋后的根节点的右孩子，右旋后的根节点原本的右孩子（黄色节点）变成了原来的根节点（红色节点）的左孩子。旋转完成后，仍然是一棵二叉排序（搜索）树。

LR旋转代码如下：

node *LeftRightRotate(node *root) {
	//先对root的左子树左旋再对root右旋 
	root->left=LeftRotate(root->left);
	return RightRotate(root);
}

代码解析：返回的是LR旋转后的根节点，先对根节点的左子树左旋，再整体右旋。root对应上图中值为9的节点。

（4）先右旋再左旋（RL）

所谓RL（先右旋再左旋）就是先将右子树右旋，再整体左旋，下图为最简洁的RL旋转（插入2导致值为1的节点不平衡）：

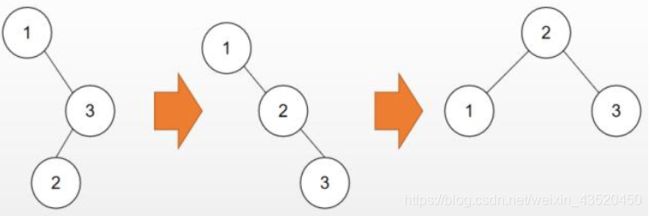
然而更多时候根节点并不是只有一个子树，下图为复杂的RL旋转（插入8导致值为4的节点不平衡）：

先将红色节点的右子树右旋，红色节点的右子树的根原本是值为9的节点，右旋后变为值为6的节点，原来的根节点变成了右旋后根节点的右孩子，右旋后根节点原本的右孩子（蓝色节点）变成了原来的根节点的左孩子；再整体左旋，原来的根节点（红色节点）变成了左旋后的根节点的左孩子，左旋后的根节点原本的左孩子（黄色节点）变成了原来的根节点（红色节点）的右孩子。旋转完成后，仍然是一棵二叉排序（搜索）树。

RL旋转代码如下：

node *RightLeftRotate(node *root) {
	//先对root的右子树右旋再对root左旋 
	root->right=RightRotate(root->right);
	return LeftRotate(root);
}

代码解析：返回的是RL旋转后的根节点，先对根节点的右子树右旋，再整体左旋。root对应上图中值为4的节点。

构造平衡二叉树是一个边插入边调整的过程，插入一个看看是否造成了不平衡，造成了不平衡就立即调整。
代码如下：

node *Insert(node *root,int v) {
	if(root==NULL) { 
	  root=new node; 
	  root->val=v; 
	  root->left=NULL; 
	  root->right=NULL; 
	}else {
	  if(v<root->val) {
	  	//插到左子树上 
	  	root->left=Insert(root->left,v);
	  	if(depth(root->left)-depth(root->right)>=2) {
	  	//左边高右边低
	  		if(v<root->left->val) {
	  		//右旋 root=RightRotate(root); 
	  	     }else {
	  	     //先对其左子树左旋再右旋root=LeftRightRotate(root); 
	  	     } 
	      } 
	  }else {
	  //插到右子树上 
	  root->right=Insert(root->right,v);
	  if(depth(root->right)-depth(root->left)>=2) {
	  	if(v>root->right->val) {
	  	//左旋root=LeftRotate(root); 
	  	}else {
	  	//先对其右子树右旋再左旋 root=RightLeftRotate(root); 
	  	   }
	       } 
	    } 
	}
     return root;
}

代码解析：出现不平衡时到底是执行LL、RR、LR、RL中的哪一种旋转，取决于插入的位置。可以根据值的大小关系来判断插入的位置。插入到不平衡节点的右子树的右子树上，自然是要执行LL旋转；插入到不平衡节点的左子树的左子树上，自然是要执行RR旋转；插入到不平衡节点的左子树的右子树上，自然是要执行LR旋转；插入到不平衡节点的右子树的左子树上，自然是要执行RL旋转。

四、AVL树的四种删除节点方式

AVL 树和二叉查找树的删除操作情况一致，都分为四种情况：

（1）删除叶子节点
（2）删除的节点只有左子树
（3）删除的节点只有右子树
（4）删除的节点既有左子树又有右子树

只不过 AVL 树在删除节点后需要重新检查平衡性并修正，同时，删除操作与插入操作后的平衡修正区别在于，插入操作后只需要对插入栈中的弹出的第一个非平衡节点进行修正，而删除操作需要修正栈中的所有非平衡节点。

删除操作的大致步骤如下：

（1）以前三种情况为基础尝试删除节点，并将访问节点入栈。
（2）如果尝试删除成功，则依次检查栈顶节点的平衡状态，遇到非平衡节点，即进行旋转平衡，直到栈空。
（3）如果尝试删除失败，证明是第四种情况。这时先找到被删除节点的右子树最小节点并删除它，将访问节点继续入栈。
（4）再依次检查栈顶节点的平衡状态和修正直到栈空。

对于删除操作造成的非平衡状态的修正，可以这样理解：对左或者右子树的删除操作相当于对右或者左子树的插入操作，然后再对应上插入的四种情况选择相应的旋转就好了。

五、平衡二叉树的性能分析

因为平衡二叉树也是二叉搜索树，回顾二叉搜索树中的操作复杂度，查询、插入和删除复杂度均为Log2N~N。平衡二叉树中查询复杂度影响因素自然为树的高度；插入节点操作可以拆分为两个步骤：查询节点位置，插入节点后平衡操作；删除节点操作同理可以拆分为两个步骤：查询节点位置，删除节点后平衡操作。

平衡调节过程中可能存在旋转操作，递归执行的次数则依赖于树的高度（可以优化为当前节点平衡因子不发生变化，则取消向上递归）。所以平衡二叉树中查询、插入和删除节点操作的复杂度依赖于树高。

平衡二叉树因为左右子树的平衡因子限制，所以不可能存在类似于斜树的情况，因为任一节点的左右子树高度差最大为一，且二叉树具有对称性，所以不妨设每个子树的左子树高度大于右子树高度。