《Progressive Learning of Category-Consistent Multi-Granularity Features for FGVC》阅读笔记

论文标题

《Progressive Learning of Category-Consistent Multi-Granularity Features for Fine-Grained Visual Classification》

细粒度视觉分类中类别一致多粒度特征的渐进学习

作者

Ruoyi Du , Jiyang Xie 北邮的大佬们

初读

摘要

• 现状：

  细粒度视觉分类（FGVC）类内对象的变化非常微妙。最近的研究主要是由部件驱动的（显式或隐式），其假设是细粒度信息自然存在于部件中。

• 本文：

  在本文中，我们采取了不同的立场，并表明严格意义上的部件操作并非必要–关键在于鼓励网络以不同粒度进行学习，并逐步将多粒度特征融合在一起。我们特别提出了：

  1. 有效融合不同粒度特征的渐进式训练策略；
  2. 鼓励网络以特定粒度学习类别一致特征的一致块卷积。

  我们在几个标准的 FGVC 基准数据集上进行了评估，结果表明所提出的方法始终优于现有的替代方法，或提供了具有竞争力的结果。

结论

• 本文从一个非常规的角度切入细粒度视觉分类问题–没有明确或隐含地挖掘对象的部分；
• 通过跨粒度学习和有效融合多粒度特征可以提取细粒度特征。
• 除类别标签外，我们的方法无需额外的手动注释即可进行训练，并且在测试过程中只需要一个具有前馈传递的网络。
• 我们在三个广泛使用的细粒度数据集上进行了实验，在其中两个数据集上取得了最先进的性能，而在另一个数据集上则具有竞争力。

再读

Section 1 INTRODUCTION

• 第一段：细粒度视觉分类现状

  • 细粒度视觉分类（FGVC）旨在识别给定对象类别的子类别。
  • 传统的分类任务通常只需整体特征即可，而细粒度类别之间的微妙差异则要求采用新颖的设计来克服类内差异。
  • 迄今为止，大多数有效的解决方案都依赖于在局部鉴别区域提取细粒度特征表征，具体做法是显式检测语义部分或隐式通过显著性定位。因此，这些具有局部区分度的特征将被集体融合，以执行最终分类。

• 第二段：从人工标注到弱监督

  • 早期的工作大多是在人工标注的帮助下找到鉴别区域。然而，人工标注很难获得，而且往往容易出错，导致性能下降。
  • 因此，研究重点转向在仅给出类别标签的情况下以弱监督方式训练模型。这些模型的成功在很大程度上归功于能够为下游分类找到更具区分性的局部区域。
  • 然而，人们很少或根本没有努力去确定：
    1. 这些局部区域在哪个粒度上最具鉴别力，例如，鸟类较细的喙或较粗的头部；
    2. 不同粒度的互补信息是否可用于更好的细粒度特征学习，例如，协同喙和头部特征是否有任何好处。

• 第三段：从简单放大到融合不同粒度特征

  • 不同粒度的信息在辨别细粒度类别时往往同时起作用。也就是说，识别独立的辨别部分往往是不够的，还需要识别这些部分是如何以互补的方式相互作用的。
  • 最近的研究侧重于 "放大 "因素，即不仅要识别各部分，还要识别每个部分中真正具有区分性的区域（例如，喙比头更有区分性）。
    • 然而，这些方法大多只关注少数几个预定义的部分，而在放大时忽略了其他部分。
    • 更重要的是，它们没有考虑如何以协同的方式将不同放大部分的特征融合在一起。
  • 与这些方法不同的是，我们进一步认为，我们不仅需要识别部件及其最具辨别力的粒度，还需要解决如何有效合并不同粒度的部件的问题。

• 第四段：本文思想

  

  • 图片注解：

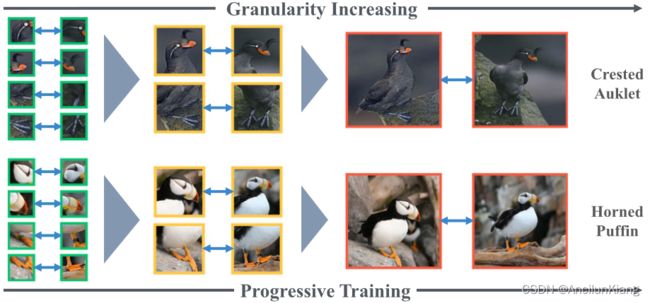
    以 CUB-200-2011 数据集为例说明 FGVC 中的多粒度信息。对于属于某一物种的鸟类（右图），可以观察到很大的类内差异（例如不同的姿态、背景和拍摄角度）。随着语义部分的粒度从右向左减小，其结构模式变得更加稳定，模式的类内变化也显著减小。

  • 如图 1 所示，我们有两个独特的关键见解：

    • 在较低的粒度水平上，辨别模式通常表现出较小的视觉差异，例如，鸟喙比鸟头表现出较小的类内差异；
    • 较粗粒度的特征可以通过学习较细粒度的特征逐步加强，例如，了解鸟喙有助于区分鸟头（即 "放大-缩小 "而不是 “放大-缩小”）。

  • 基于这些见解，本文不会明确或隐含地试图从部件（或其放大版本）中挖掘精细特征表征。相反，本文假设细粒度的判别信息自然存在于不同的视觉粒度中–这就是鼓励网络以不同的粒度进行学习，并同时协同多粒度特征。

• 第五段：综合框架概述

  本文提出了一个可同时容纳部分粒度学习和跨粒度特征融合的综合框架，通过两个相互协同工作的组成部分来实现的：

  • 有效融合不同粒度特征的渐进式训练策略；
  • 鼓励网络在特定粒度上学习类别一致特征的类别一致块卷积 (CCBC)。请注意，我们没有使用 "比例 "一词，因为我们并没有在图像斑块上应用高斯模糊滤波器，而是将特征图平均划分为不同的粒度级别。

• 第六段：多粒度渐进式训练框架

  • 目的：

    作为第一个贡献，我们提出了一个多粒度渐进式训练框架，以学习不同粒度的互补信息。

  • 训练过程：

    • 我们的渐进式框架在训练过程中分步进行，每一步的训练都侧重于培养特定粒度的信息。
    • 我们从更稳定的细粒度开始，然后逐渐过渡到更粗的粒度。这类似于 "放大 "操作，即网络可以先聚焦于一个小区域，然后放大到这个局部区域周围的更大片段，最后再放大到整个图像。
    • 更具体地说，在每个训练阶段结束时，当前阶段学习到的参数将作为参数初始化传递给下一个训练阶段。这种传递操作本质上是让网络在学习更粗粒度的特征时利用更细粒度的特征。最后，所有阶段的预测结果都会合并在一起，以进一步确保互补信息得到充分利用。

• 第七段：类别一致块卷积提出的动因

  • 天真地应用渐进式训练并不能保证多粒度特征学习。这是因为通过渐进式训练学习到的细粒度信息往往会集中在相似的区域。
  • 在我们早期的研究中，我们通过引入拼图生成器来解决这个问题，在每个训练步骤中形成不同的粒度级别。从本质上讲，它迫使网络的每个阶段都关注局部斑块，而不是整个图像的整体，从而学习特定粒度级别的特定信息。
  • 虽然这种方法在鼓励模型关注细粒度的视觉细节方面很有效，但进一步的研究表明，拼图策略也会引入与自然图像统计不一致的人为边界，否则对特征学习会适得其反–模型需要同时关注此类 "信息丰富 "的边界区域（见第 4.5.4 节）。

• 第八段：类别一致块卷积 (CCBC)

  

  • 图片注解：

    拟议的类别一致块卷积（CCBC）操作。这里，我们以将一个特征图分割成 $4\times 4$ 个块为例。对于建议的分块卷积，首先要将特征图分割成大小相同的块。我们只在每个区块内进行卷积处理，这意味着输出的所有元素只能接收来自所属区块的信息。然后，给定一对属于同一类别的图像，我们从它们的每个通道中选择最突出的块，并相应地限制它们保持一致，从而鼓励网络关注与类别相关的区域。请注意，整个过程发生在每个通道上，我们仅以两个通道为例进行简要说明。

  • 本文扩展了之前的方法，采用一种新颖的类别一致块卷积（CCBC）模块来解决这些问题，该模块由块卷积操作和类别一致约束组成。

  • 就块卷积模块而言，特征图在训练阶段被发送到每个卷积层之前，会被分割成若干块。每个块都不能通过卷积操作获取相邻块的信息。这种操作既能保持拼图训练的优势，又不会引入人为的边界。

  • 在特征块内进行卷积时，为了进一步捕捉每个粒度上有意义的区域，我们在块卷积操作的同时应用了类别一致性约束。具体来说，我们对每个类别的图像进行成对采样，然后在块卷积过程中对其突出块进行类别一致性约束，从而有效地鼓励网络关注类别内共享的共同区域（即前景）。

  • 需要注意的是，虽然通过成对约束来减少类内差异似乎是一种直观而通用的解决方案，但由于存在人为边界（见第 4.4.2 节），它无法独立地与我们之前的框架配合使用。

• 总结 本文贡献有三个方面：

  • 我们介绍了一种渐进式训练策略，它以 "放大 "的方式处理细粒度视觉分类任务。它通过不同的训练步骤来促进特征学习过程，最终培养出不同粒度的固有互补特性。
  • 我们提出了一种类别一致的分块卷积（CCBC），它将分块卷积操作与特征类别一致性约束相结合。一方面，通过控制特征粒度，分块卷积保证了每一步都能学习到更精细的特征。另一方面，类别一致性约束可以防止过拟合问题，并确保捕捉到的多粒度区域是有意义和与类别相关的。
  • 我们在四个广泛使用的 FGVC 数据集上进行了实验：CUB-200-2011、NA-Birds、Stanford Cars 和 FGVC-Aircraft。所提出的方法在所有这些数据集上都达到了最先进（SOTA）或具有竞争力的性能。广泛的烧蚀研究和可视化效果证明了我们设计的有效性。

Section 2 RELATED WORK

2.1 Fine-Grained Visual Classification

细粒度视觉分类

• 由于 FGVC 与传统的粗粒度分类任务之间存在巨大差距，CNN 在细粒度分析方面的优势仍然有限。
• 为了寻找精细表征，之前的许多方法都侧重于更好、更有效地定位具有区分性的物体部分。
  • Zhang 等人采用了物体检测（即 R-CNN）来定位局部区域，以便提取特征。
  • Krause 等人指出了部分注释的局限性，并采用协同分割方法，以弱监督的方式裁剪物体部分。
  • Zheng 等人进一步指出，检测和细粒度特征学习可以相互促进。有几种方法并不是简单地定位具有区分度的部分，而是试图从多粒度的部分中挖掘互补信息。除了对定位部分进行裁剪外，
  • Zheng 等人还利用基于注意力的非均匀采样器来突出感兴趣的部分。
  • Ding 等人也指出了忽略周围环境的局限性，并对选定的信息区域采用了非均质变换。
  • Wang 等人精心设计了一组滤波器，作为隐含捕捉判别模式的部分检测器。
  • 除了独立利用区域特征外，Wang 等人还将具有辨别力的区域聚合成组，并进一步从区域相关性中挖掘辨别潜力。最近，来自其他模态的知识也被考虑在内。
  • Song 等人不仅分阶段捕捉了多个判别部分，还利用文本描述中的知识进行了交互式配准。
• 本文工作的早期和初步版本出现在文献中，该文献鼓励模型在渐进式训练计划中从多粒度拼图中挖掘多粒度信息。然而，天真地使用拼图斑块进行训练会导致一些局限性：
  • 拼图斑块会在训练过程中引入人为边界，
  • 拼图斑块会使特征学习复杂化，模型可能无法捕捉到有意义的区域。
• 与早期工作相比，本研究的不同之处在于：
  • 我们提出了一种名为 "类别一致的块卷积（CCBC）"的替代解决方案，用于在不引入人为边界的情况下控制特征粒度。同时，在类别一致的约束下，可以防止无意义的区域被聚焦。
  • 增加了大量的实验和分析，以更好地证明所提方法的有效性和泛化能力。

2.2 Progressive Training Scheme

渐进式训练策略

• 渐进式训练首次出现在图像生成任务中。它的灵感来源于以前的具有多个生成器或判别器的生成对抗网络（GAN）。它试图从低分辨率图像开始，然后通过向网络添加新层来逐步提高图像分辨率，从而降低生成式对抗网络的训练难度。它使网络不再学习生成整个图像，而是首先学习全局结构，然后再提供那些困难的更精细的细节。
  • Shaham 等人提出了一种无条件的单幅图像 GAN 方案，该方案从单幅图像的多尺度分布中学习。最近，Wang 等人在超分辨率重建任务中采用了渐进式思想，该模型在结构和训练方案上都是渐进式的，可以在大的上采样因子下很好地工作。
  • Ahn 等人在中也引入了渐进式训练方案，用于在超分辨率重建任务中逐步添加级联残差块，以生成分辨率更高的图像。
• 上述所有作品都只关注图像生成任务。在本文中，我们利用渐进式训练的一般概念来解决 FGVC 问题。最显著的不同之处在于：
  • 我们不使用低分辨率和高分辨率，而是在不同粒度的斑块之间进行渐进训练；
  • 我们从更精细的细节（较小的斑块）开始，逐步过渡到更全面的细节（较大的斑块），而不是从粗到细。

Section 3 METHODOLOGY

3.1 Overview of The Proposed Method

拟议方法概述

• 对于 FGVC 任务而言，直接关注图像的全局结构会引入因类内变化大而导致的不稳定性，从而增加训练难度。

• 人们普遍认为，解决 FGVC 任务问题的关键在于从局部区域挖掘辨别信息。在这项工作中，我们不再以 “放大”（zooming-in）的方式识别物体（例如，先定位辨别部分，然后从中提取局部特征），而是根据两种见解提出了一种新颖的 "缩小 "框架：

  • 当判别模式的粒度降低时，判别模式往往更加稳定；
  • 小粒度模式的学习可以促进大粒度模式的学习。

• 具体来说，我们的方法可大致分为两部分。

  • 首先，我们通过渐进式训练程序来学习细粒度信息。
    • 一般来说，CNN 的较浅阶段代表局部细节，而较深阶段则主要表示颗粒度更大的抽象语义。
    • 因此，作为一种直观的选择，我们首先让网络在较浅的阶段挖掘更精细的分辨特征，然后根据预先学习到的知识（在较浅阶段获得的知识），逐步将注意力转移到粒度更大的模式上。
    • 在这种情况下，可以有效避免直接学习整个对象时由于类内差异造成的弊端。
  • 其次，为了促进渐进式训练过程中的多粒度学习，我们提出了一个类别一致的块卷积（CCBC）模块，
    • 该模块由两个高度耦合的部分组成：块卷积操作和类别一致约束。
    • 在每个训练步骤中，特征图在空间上被分割成多个区块，卷积层只在每个特征区块内运行。这样，通过将卷积层的感受野限制在小于其理论大小的范围内，可促使网络专注于特定的粒度。
    • 然后，在每个通道中选择响应最高的区块，并将其聚合起来形成一个鉴别特征嵌入，它代表了在特定粒度上挖掘的鉴别信息。属于同一类别的特征嵌入对的距离会强制变小，以确保它们与类别相关。

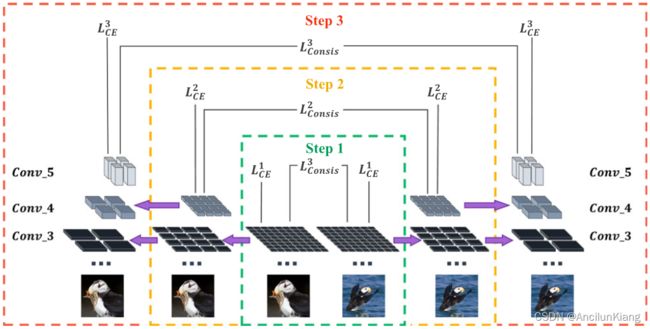
• 总之，渐进式训练策略实现了从局部到全局的学习过程，而 CCBC 则保证了在每个训练步骤中都能学习到类别一致的多粒度特征。整个框架如图 3 所示，各部分的设计细节将在第 3.2 和 3.3.1 节中详细阐述。

  

• 图片注解：

  随着训练过程的不断深入，训练阶段会越来越深，不同阶段的特征块尺寸也会越来越大。这里，我们以最后三个阶段为例，采用渐进式训练策略，即训练步数为 $P=3$。每一步的超参数 $n$ 分别设置为 $8$、$4$ 或 $2$。相同颜色的特征图表示各阶段共享相应卷积核的权重，紫色箭头表示两步之间从较小粒度级别到较大粒度级别的知识转移。图中省略了额外的卷积层和包括分类器在内的全连接层。

3.2 Progressive Training

渐进式训练

3.2.1 Network Architecture

网络结构

我们用于渐进训练的网络设计是通用的，可以在任何 CNN 架构之上实现。一个 CNN 的结构可分为几个阶段，每个阶段由一组级联卷积层组成（例如，ResNet 可分为五个阶段：从 $Conv(1)$ 到 $Conv(5)$）。对于包含 $S$ 个阶段的特征提取器，$X^{Conv(s)}\in R^{T\times W\times H\times C}$，$s=1,\dots ,S$（$T$、$W$、$H$ 和 $C$ 分别为特征图的批量大小、宽度、高度和通道数）表示第 $s$ 阶段输出的特征图。在这里，我们的目标是对不同中间阶段提取的特征图施加分类损失。因此，我们加入了额外的卷积块 $H_{conv}^{Conv(s)}$ 和全连接层 $H_{fc}^{Conv(s)}$ 来处理从每个阶段提取的特征，使其作为分类器一起工作。

具体来说，分类器由两个卷积层和两个采用 BatchNorm 的全连接层组成。$Conv(s)$ 的 $M$ 级最终输出 $V^{Conv(s)}\in R^{T\times M}$ 可以表示为：
$$V^{Conv(s)}=H_{fc}^{Conv(s)}\left(H_{conv}^{Conv(s)}\left(X^{Conv(s)}\right)\right)$$

3.2.2 Training Procedure

训练程序

在训练阶段，一次迭代包含几个步骤，依次优化每个阶段的输出。由于低级阶段的感受野和表征能力有限，网络将被迫首先利用局部细节（即物体纹理）中的判别信息。这样，阶梯式增量训练自然就能让模型从局部细节开始挖掘辨别信息，当特征逐渐被传送到更高级的阶段时，就会逐渐形成更全面的结构。

需要注意的是，根据第 4.4 节的实验结果，与其利用所有 $S$ 个阶段进行渐进式训练，还不如利用最后 $P$ 个阶段来得更好。这是因为低级阶段主要代表与类无关的模式，这些模式会受到上述 FGVC 监督的损害。与参与渐进式训练的阶段数相等，一次迭代有 $P$ 个步骤，对应 $P$ 个输出，即 $\left[V^{Conv(S-P+1)},\dots ,V^{Conv(s)},\dots ,V^{Conv(s)}\right]$ 每个输出都通过交叉熵（CE）损失进行优化，即
$$\begin{array}{rl}{\mathcal{L}}_{CE}^p& ={\mathcal{L}}_{CE}\left(V^{Conv(S-P+p)},Y\right)\\ & =-\frac{1}{T}\sum _{t=1}^T\sum _{m=1}^M{Y}_{t,m}\log \left(V_{t,m}^{Conv(S-P+p)}\right)\end{array}$$
其中，$Y$（$T\times M$ 维）的每一行都是这批输入中相应样本的单次标签。

3.3 Consistent Block Convolution

一致的块卷积

3.3.1 Block Convolution

分块卷积

通过渐进式训练策略，我们希望网络能够根据网络感受野的变化，从更细到更粗的层次挖掘多粒度信息。然而，由于高级深度卷积神经网络的感受野较宽，因此效果有限（例如，对于 ResNet50，当输入图像大小设置为 $448\times 448$ 时，理论感受野为 $291\times 291$ 和 $483\times 483$ 的 $Conv(4)$ 和 $Conv(5)$ 均能覆盖目标对象的主要部分）。为了解决 FGVC 的这一缺点，我们提出了一种块卷积操作，鼓励网络关注局部特征，同时保持深度架构的强大表示能力。分块卷积操作可以在任何广泛使用的骨干网络上实现，无需改变网络架构或引入额外参数。

设 $X^l\in {\mathbb{R}}^{T\times W\times H\times C},l\in [1,L]$ 为第 $l$ 个卷积层的输出，其中 $L$ 为卷积层的总数。那么一般的卷积操作（带填充）可以表示为：
$$X^{l+1}=\mathcal{F}(X^l,{\mathcal{W}}^{l+1})$$
其中，$X^{l+1}$ 是输出特征图，${\mathcal{W}}^{l+1}$ 是卷积层 $l+1^{st}$ 的权重。

对于提议的块卷积，输入特征图首先被分割成 $n\times n$ 个大小相等的块数组，如下所示：
$$\begin{array}{rl}\mathcal{B}(X^l)& =[X_{1,1}^l,\dots ,X_{i,j}^l,\dots ,X_{n,n}^l],\\ X_{i,j}^l& \in R^{T\times \frac{W}{n}\times \frac{H}{n}\times C}\end{array}$$
其中，$i,j\in \{1,\dots ,n\}$ 是特征块 $X_{i,j}^l$ 的纵向和横向索引，超参数 $n$ 定义了每个维度的特征块数量，反过来又控制了当前步骤可学习模式的粒度。我们在每个特征块内使用共享参数 ${\mathcal{W}}^{l+1}$ 进行卷积，然后将其还原为 $X^{l+1}\in R^{T\times W\times H\times C}$，即
$$\begin{array}{rl}{X}_{i,j}^{l+1}& =\mathcal{F}(X_{i,j}^l,{\mathcal{W}}^{l+1})\\ X^{l+1}& =\mathcal{R}(X_{1,1}^{l+1},\dots ,X_{i,j}^{l+1},\dots ,X_{n,n}^{l+1})\end{array}$$
这里的 $\mathcal{R}(\cdot )$ 是还原操作。这样，我们就限制了网络所能捕捉到的信息区域的大小，使其不大于 $\frac{W}{n}\times \frac{H}{n}$，并迫使网络从局部区域挖掘辨别模式。

需要注意的是，虽然块卷积可以保证所有保留模式的粒度都小于块的大小，但并不是所有符合条件的模式都能被保留下来，因为它们可能会被块边界分割开来。当块边界总是构造在相同位置时，这种现象会对模型训练造成损害，因为它会导致一些模式永远学不到。因此，我们需要在每次迭代中在不同位置分割特征图。幸运的是，一种名为 "随机裁剪 "的常规数据增强过程可以通过对输入图像进行随机移动来实现这一功能。

将 $T\times W\times H\times C$ 维特征图分割成块，并将其连接成大小为 $(n^{2}T)\times \frac{W}{n}\times \frac{H}{n}\times C$ 的特征图，就可以很容易地实现所提出的分块卷积。此外，与其在每个卷积层之前、每个阶段重复拆分特征图，我们可以在开始时拆分特征图，并在所有卷积操作完成后恢复特征图。如果没有其他需要全局信息的附加组件（如非本地网络），可以采用这种实现方式，以提高效率。

3.3.2 Category-Consistency Constraint

类别一致性约束

块卷积通过突出每个样本中的稳定特征来削弱类内差异的影响。在这里，我们进一步应用了成对类别一致性约束，以减少同一类别样本之间的差异。具体来说，我们修改了数据加载策略，在训练过程中以成对的方式批量加载图像，即 $Y_{2i-1}=Y_{2i},i\in [1,\frac{T}{2}]$。然后，我们最小化成对图像中特征嵌入之间的欧几里得距离。

成对类别一致性约束可以与我们提出的框架很好地配合。在第 $p$ 步，给定特征图 $F^{Conv(S-P+p)}\in R^{(n_p{)}^2\times \frac{W}{n_p}\times \frac{H}{n_p}\times C}$ 从 $Conv(S-P+p)$ 的最后一个块卷积层中提取，$n^p$ 是第 $p$ 步设置的超参数 $n$。我们首先应用分块平均池化层 $AvgPool(\cdot )$ 来聚合每个分块的特征，然后选择每个通道的最大响应值（$Max(\cdot )$）作为特征嵌入 $E^{Conv(S-P+p)}$ 如下：
$$E^{Conv(S-P+p)}=Max(AvgPool(X^{Conv(S-P+p)}))\in R^C$$
然后，我们将上述属于同一类别的一对嵌入之间的欧氏距离作为类别一致性约束的损失函数：
L C o n s i s p = ∑ i = 1 T 2 ∣ E 2 i − 1 C o n v ( S − P + p ) − E 2 i C o n v ( S − P + p ) ∣ 2 \mathcal{L}^p_{Consis}=\sum^{\frac{T}{2}}_{i=1}\left|E^{Conv(S-P+p)}_{2i-1}-E^{Conv(S-P+p)}_{2i}\right|^2 LConsisp​=i=1∑2T​​ ​E2i−1Conv(S−P+p)​−E2iConv(S−P+p)​ ​2
第 $p$ 级的总损耗可表示为：
$${\mathcal{L}}_{Total}^p={\mathcal{L}}_{CE}^p+{\lambda }_p{\mathcal{L}}_{Consis}^p$$
其中 ${\lambda }_p$ 是一个超参数，用于平衡两种损失的权重。

3.4 Inference

推论

**在推理阶段，可以移除上述所有组件。块卷积运算可以简单地替换为一般卷积运算，因为模型已经学会了识别局部模式，没有必要对特征图保留任何约束。**在这种情况下，虽然我们的框架延长了训练时间，但推理效率不会受到影响。为了利用各个阶段互补的多粒度知识，我们将所有输出的平均值合并在一起，得到最终结果 $V$，即：
$$V=\frac{1}{P}\sum _{p=1}^P{V}^{Conv(S-P+p)}$$
第 4.4 节分析了每种输出及其不同组合的性能，并展示了利用多粒度信息的互补性所获得的性能。

Section 4 EXPERIMENTAL RESULTS AND DISCUSSIONS

实验结果与讨论

在本节中，我们在第 4.1 节讨论的四个广泛使用的 FGVC 数据集上进行了实验；表 1 列出了这些数据集的详细统计数据。第 4.2 节提供了所提方法的实现细节。随后，第 4.3 节展示了模型与其他最先进方法的性能比较。为了说明我们方法中不同组件和设计选择的有效性，第 4.4 节提供了全面的消融研究和讨论。此外，第 4.5 节还展示了不同设置下模型的可视化效果，以便更好地理解我们的模型是如何工作的。

4.1 Datasets

数据集

我们在 CUB-200-2011、NA-Birds、Stanford Dogs、Stanford Cars 和 FGVC-Aircraft 数据集上对所提出的方法进行了评估，简要介绍如下：

• CUB-200-2011 (CUB)是最具挑战性和最受欢迎的 FGVC 数据集之一。鸟类姿态（如飞鸟、游鸟和站在树枝上的鸟）、生长阶段（如雏鸟和成鸟）和背景环境（如森林、海洋和天空）的多样性导致鸟类全局结构的类内差异很大。此外，对于同属一个家族的鸟类（如不同种类的麻雀或海鸥），即使是许多专家也无法在视觉上将它们区分开来，这就使得在现有先进技术的基础上进一步提高识别率变得十分困难。
• NA-Birds（NAB）是最近提出的一个具有高质量注释和大规模图像的 FGVC 数据集。与 CUB-200-2011 数据集相比，它包含的带有类别标签和边界框注释的图像数量是后者的三倍。他们还提供了一个以 AlexNet 作为特征提取器并利用所有注释的基线，其准确率达到了 75:0%。在此，我们也在 NA-Birds 上对我们的方法进行了评估，在训练和测试阶段只使用了类别标签。
• 斯坦福狗（Stanford Dogs，DOG）是一个大规模数据集，由 120 种狗组成。与其他 FGVC 数据集类似，该数据集也存在较小的类间差异和相对较大的类内差异。例如，这些图像可能包含不同年龄、姿势和颜色的狗。此外，作为人类的友好伙伴，这些图像主要来自日常生活照片，这为我们评估我们的方法提供了一个互补的场景。
• 斯坦福汽车（Stanford Cars，CAR）是一个由 196 类汽车组成的数据集，这些汽车在品牌、型号和年份上通常各不相同。数据收集自自然图像和渲染图像，这导致了背景的多样性和主要对象的不同比例。虽然汽车的形状和结构比鸟类更为严谨，但由于外观（如颜色）造成的类内差异较大，因此该数据集仍然具有挑战性，同时也代表了一种互补的情况。
• FGVC-Aircraft (AIR) 是一个旨在区分不同型号飞机的数据集。与对鸟类等动物进行分类不同，对具有刚性结构的飞机进行分类面临着由于其他原因（如不同航空公司的飞机涂装不同）造成的类内差异。因此，许多研究人员广泛使用这种方法来展示他们的方法在处理任何类型的 FGVC 任务时的泛化能力。

4.2 Implementation Details

实施细节

• 我们在 GTX2080Ti GPU 集群上使用版本高于 1.4 的 PyTorch 进行了所有实验。
• 这些网络的阶段总数为五个。为了获得最佳性能，我们让最后三个阶段进行渐进式训练，即训练步骤数 $P=3$。
• 对于这三个训练步骤，我们分别设置 $n=8$、$4$ 或 $2$，${\lambda }_p=0.01$、$0.05$ 或 $0.1$。
• 在训练阶段，只引入类别标签。输入图像被调整为固定大小，然后随机裁剪为 $448\times 448$。
• 在训练网络时，我们会随机应用水平翻转来增加数据。在推理阶段，输入图像被调整大小，然后居中裁剪为 $448\times 448$。
• 上述所有设置都是文献中的标准设置。
• 我们使用随机梯度下降法（SGD）的动量优化器和批量归一化作为正则化器。
• 同时，与文献类似，我们为每个数据集设置了最佳学习率。新添加的卷积层和 FC 层的学习率初始化为 $0.005$，预训练骨干层的学习率保持为新添加层的 $1/10$。
• 对于上述所有模型，我们最多训练了 200 个 epoch，批量大小为 $32$，权重衰减为 $0.0005$，动量为 $0.9$。对于上述所有模型，在第 100 次和第 150 次 epochs 时，学习率乘以 $0.1$。

4.3 Comparisons With State-of-the-Art Methods

与 SOTA 方法的比较

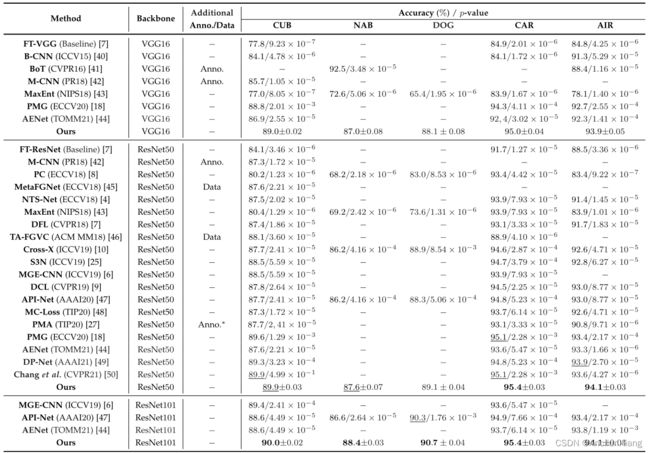
我们在上述数据集上使用三种流行的骨干架构对所提出的方法进行了评估： VGG16、ResNet50 和 ResNet101 。比较结果如表 2 所示。根据骨干网络的不同，该表分为三组。除了 top-1 准确率外，我们还列出了我们的方法与最先进方法之间的单样本学生 t 检验的 p 值，假设是在相同骨干网络下两个种群的均值相等。由于所有相应的 p 值均小于 0.05，因此从统计学角度看，所提出的方法比上述技术有显著的性能提升。详细分析如下。

图片注解：

• 在 CUB-200-2011 (CUB)、NA-Birds (NAB)、Stanford Dogs (DOG)、Stanford Cars (CAR) 和 FGVC-Aircraft (AIR) 数据集上与其他最新方法的比较。
• 最佳结果用粗体标出，次佳结果用下划线标出。在两个群体均值相等的零假设下，列出了我们的方法与其他最先进方法的准确度之间的单样本学生 t 检验的 p 值。显著性水平设定为 0.05。额外注释/数据： 额外注释/数据。仅在 CUB 数据集上使用了附加数据（文本描述）。

4.3.1 Performance on CUB-200-2011

比较结果见表 2。根据所使用的骨干网络，该表分为三组。我们的方法在不同骨干网络下的表现优于所有先进方法，这表明了它的优越性和鲁棒性。特别是，与流行的基于部件的方法相比，所提出的方法在没有显式或隐式定位辨别部件的情况下，平均提高了 $2.2\%$。即使与利用部件注释的 M-CNN 和引入文本描述的 PMA 相比，我们的方法在仅使用类别标签进行训练时仍然超过了它们。MetaFGNet 指出了细粒度数据的局限性，并提出了一种基于元学习的方法，以获得特定细粒度任务的最佳网络参数。然而，在以 ResNet50 为基础模型的情况下，我们的方法以 $2.3\%$ 的优势超过了它，这表明我们的方法在有限的训练数据下具有很强的泛化能力。

4.3.2 Performance on NA-Birds

作为一个大规模数据集，NA-Birds 的类别数量是 CUB-200-2011 的两倍多，这使其更具挑战性。不过，如表 2 所示，我们的方法仍能在该数据集上获得最先进的结果，这表明我们的模型在不同数据集规模和类别数量下都具有鲁棒性。虽然 Cross-X 也利用了多阶段特征来利用它们之间的关系，但我们仍然以 $1.4\%$ 的优势超过了它，这表明了以渐进方式学习多粒度特征的优越性。此外，当我们用 ResNet50 代替 VGG16 作为基础模型时，所提方法的性能提高了 $0.6\%$，而当配备 ResNet101 时，性能进一步提高了 $0.8\%$。这表明，当数据集的规模很大时，所提出的方法可以从更深的 CNN 架构中获益更多。

4.3.3 Performance on Stanford Dogs

斯坦福狗作为一个已存在十多年的数据集，作为 FGVC 的常用基准，在很大程度上被忽视了，只有极少数论文报告了相关结果。由于缺乏前人的努力，我们在所有三个骨干网络上都获得了最先进的性能，这并不令人惊讶。此外，与在 NABirds 上取得的结果类似，与其他三个常用数据集相比，当采用更深的 CNN 架构时，所提出的方法能带来更大的性能提升。我们将此归因于更大规模的数据集决定了网络具有更好的表征学习能力。这可能表明，在 FGVC 文献中，像 NA-Birds 和 Stanford Dogs 这样的大规模数据集不应被忽视，因为它们提供了解决问题的不同视角。

4.3.4 Performance on Stanford Cars

当以 VGG16 作为骨干网络时，由于渐进式训练策略使梯度更容易传播到浅层，并起到了跳过连接的作用，因此所提出的方法出人意料地超过了 FT-VGG（即基线模型）$10.1\%$。与效果良好的微调 ResNet50 相比，它还提高了 $3.4\%$。我们利用所有这些骨干网络（VGG16、ResNet50 和 ResNet101）获得了最先进的性能，这进一步表明我们的渐进式多粒度训练策略可用于任何先进的网络架构，以提高性能。虽然 BoT 利用了物体边界框注释，但在骨干网络相同的情况下，我们的方法仍比它高出 $2.5\%$。需要注意的是，与我们之前的版本相比，新提出的方法平均提高了 $0.5\%$，这说明了去除人为边界和引入类别一致性约束所带来的好处。

4.3.5 Performance on FGVC-Aircraft

即使与其他最先进的方法（这些方法利用了额外的文本描述或方框注释）相比，所提出的方法也获得了更好的性能，至少有 $0.7\%$ 的余量。与斯坦福汽车数据集上的结果类似，新提出的方法也明显优于我们之前的版本，VGG16 和 ResNet50 分别提高了 $1.2\%$ 和 $0.7\%$。这是因为这些刚性物体（如汽车和飞机）更容易受到同样具有刚性形状的人工边界的影响。

4.4 Ablation Studies and Discussions

消融研究与讨论

在本节中，我们首先对所有五个数据集进行消融研究，以验证每个关键组件的贡献（第 4.4.1 节），并证明其优于我们之前的工作（第 4.4.2 节）。然后，我们进行了一系列详细实验，试图阐明我们的设计选择背后的原因（请参阅第 4.4.4、4.4.5、4.4.6 和 4.4.7 节）。

4.4.1 Effectiveness of Each Component

各组成部分的效果

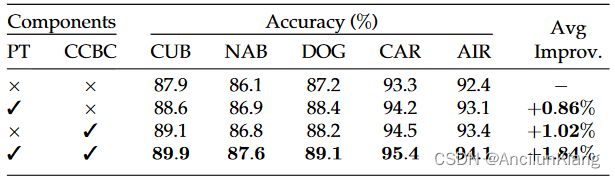
图片注解：消融研究。列出并讨论了渐进式训练（PT）策略和类别一致块卷积（CCBC）的有效性。最佳结果以粗体标出。

如表 3 所示，我们以 ResNet50 为骨干网络在五个数据集上进行了实验，以验证每个组件的有效性。如果去掉渐进式训练策略和类别一致的块卷积，则只需训练具有多级输出的模型，并在推理时将其预测结果合并即可得到结果。虽然简单地组合多级输出就能获得良好的性能，但渐进式训练策略提高了模型的准确性，平均幅度为 $0.86\%$，这表明简单的局部到全局学习过程可以促进细粒度特征学习。此外，即使只采用渐进式训练策略的模型准确率（如在 CUB-200-2011 数据集上为 $88.6\%$）已经超过了大多数流行方法，CCBC 还能进一步提高模型性能，在所有五个数据集上平均提高 $0.98\%$。这种进一步提高表明了仅以渐进方式进行训练的局限性，同时也表明了突出多粒度和类别相关特征的有效性。

4.4.2 Jigsaw Patches versus Category-Consistent Block Convolution

拼图补丁与类别一致的块卷积

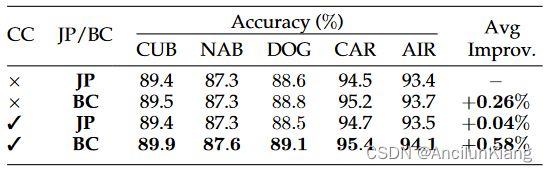
图片注解：

• 使用拼图片段 (JP) 和块卷积 (BC) 训练的模型性能比较
• 有/无类别一致性（CC）约束的结果均已列出。最佳结果以粗体标出

在本节中，我们将对拼图补丁和块卷积进行消融研究，以证明去除人为边界所带来的好处。然后，我们将进一步研究类别一致性约束与新提出的块卷积之间的耦合关系。表 4 列出了使用 ResNet50 作为骨干网络的实验结果。在没有类别一致性成对约束的情况下，用块卷积替换拼图补丁可以在一定程度上提高模型的性能，平均提高幅度为 $0.26\%$。这一性能提升表明，去除拼图补丁造成的人为边界后，模型学习会略有受益。需要注意的是，斯坦福汽车数据集和 FGVC 飞机数据集的性能提升要比两个鸟类数据集显著得多。我们认为这是因为汽车和飞机的形状比较僵硬，更容易受到人工边界的影响，而人工边界的形状也很僵硬。

此外，我们还在训练步骤中引入了类别一致性约束，以鼓励模型关注每个类别中一致的判别特征，而采用分块卷积的模型则取得了进一步的改进。然而，在使用拼图补丁进行特征粒度控制时，类别一致性约束带来的好处有限，在 CUB-200-2011 数据集上的性能甚至有所下降。我们认为，这是由于拼图补丁引入的人为边界具有高度一致性，一致性约束会错误地迫使模型关注这些无意义的边界，最终削弱了模型的有效性。相比之下，**分块卷积不仅能保持对所学特征粒度的控制能力，还能使类别一致性约束组件进一步提高模型性能。**因此，在所提出的 CCBC 中，渐进式训练策略和类别一致性约束是紧密结合在一起的。

4.4.3 Efficiency of Category-Consistent Block Convolution

类别一致的块卷积效率

值得注意的是，我们只在训练阶段使用 CCBC，它不会影响模型的推理效率。正如第 3.3.1 节所介绍的，分块卷积有两种实现方法：

• 在每个卷积层对特征图进行分割和还原；
• 在每个网络阶段对特征图进行一次分割和还原。

第一种实现方式需要进行 $(2\times n\times L)$ 次分割和恢复操作，第二种实现方式需要进行 $(2\times n\times S)$ 次此类操作，其中 $L$ 是卷积层数，$S$ 是网络级数（$L\gg S$）。关于 $n$，两种实现方式的计算复杂度均为 $O(n)$。在本节中，我们将进一步研究这两种实现方法在不同块数 $n$ 的实际训练过程中的计算成本，如图 6 所示。当 $n=1$ 时，分块卷积等同于传统卷积，计算成本随着超参数 $n$ 的增加而增加，这表明了分块卷积带来的时间预算。可以看出，两种实现方式的额外时间成本呈线性增长，与它们的时间复杂度 $O(n)$ 相呼应。此外，与 "Imp. 1 "相比，"Imp. 2 "带来的时间预算可以忽略不计，是可以接受的。

图片注解：图示块卷积随超参数 n 的增加而增加的时间成本。"Imp.1 "和 "Imp.2 "代表两种实现方式。

4.4.4 Number of Stages for Progressive Training

渐进式训练的阶段数

图片注解：不同超参数 P 的性能

在此，我们将讨论用于渐进式训练的阶段数 $P$。实验在 CUB-2002011 数据集上进行，其他设置保持不变。ResNet50 被用作骨干网络，这意味着阶段总数 $S=5$ 和 $P\in [1,5]$。由于 ResNet50 的第一级仅由一个卷积层组成，且 $P=1$ 时没有渐进训练，因此表 5 仅显示了 $P\in [2,3,4]$ 的性能。我们可以观察到，当 $P=2$ 和 $3$ 时，渐进式训练策略能如我们所愿持续提升模型性能。然而，当我们设置 $P=4$ 时，也就是 $Conv(2)$ 参与渐进式训练过程时，测试准确率显著下降了 $0.9\%$。我们认为，$Conv(2)$ 中浅层的主要目的是识别一些与类别无关的基本模式（如一些几何形状）。然而，额外的中间监督会迫使这些层挖掘与类相关的特征，从而影响整个模型的学习。因此，我们在最终设计中采用了 $P=3$。

4.4.5 Effectiveness of Output Combinations

产出组合的有效性

图片注解：以 ResNet50 为骨干网络的不同输出组合性能

为了更好地了解所提方法的有效性，我们在表 6 中列出了各阶段分类器及其不同组合的测试准确率。在所有数据集上，$Conv(5)$ 单分类器的测试精度都超过了基线（FT-ResNet50）和表 2 中列出的一些最先进的方法，这进一步证明了采用渐进式训练策略的分块卷积可以改善细粒度特征学习。当我们把多输出集合结果作为最终预测结果时，由于利用了不同粒度的互补信息，模型的性能达到了一个新的水平。尽管 $Conv(3)$ 分类器的性能较差，但它也提供了有用的信息，提高了 CUB-200-2011 和斯坦福汽车数据集的测试准确率。对于 FGVC-Aircraft 数据集中的飞机，其刚性结构和巨大尺寸使得小粒度部分的效果较差，只有 $Conv(4)$ 和 $Conv(5)$ 可以达到最佳性能。

4.4.6 Effectiveness of n at Each Stage

各阶段的成效

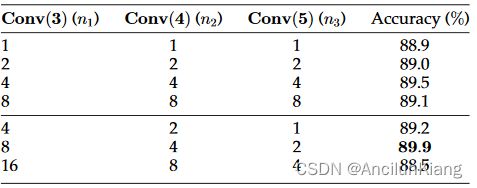
图片注解：每个步骤不同 $n$ 的性能

我们将讨论超参数 $n$ 在每个阶段的影响。如表 7 上半部分所示，当我们在所有步骤中保持相同的 $n$ 时，测试精度随着 $n$ 的增加而不断提高，直到 $n=8$。这验证了我们的假设，即更细的粒度会带来更稳定的模式，从而提高表征学习能力。我们还观察到，当 $n=8$ 时，模型的性能会下降。其中一个可能的原因是极细粒度区域的判别能力有限，这说明利用多粒度特征是足够的。

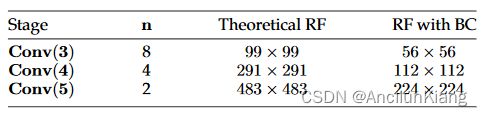
图片注解：各阶段使用普通卷积的理论接收场 (RF) 和使用拟议的块卷积 (BC) 的相应接收场 (RF) 演示

在表 7 的下半部分，我们以指数递减的方式设置了 $n$，这意味着当我们训练网络的不同阶段时，$n$ 是不同的。这可以让网络在已经学习到的更精细模式的基础上学习更粗糙的模式。根据实验结果，当我们为 $Conv(3)$、$Conv(4)$ 和 $Conv(5)$ 分别设置 $n_i,n_2,n_3=\{8,4,2\}$ 时，可以获得最佳性能。表 8 列出了以 ResNet50 为骨干、输入分辨率为 $448\times 448$ 时，当 $n=\{8,4,2\}$ 时的理论感受野和采用分块卷积的感受野。很明显，我们的分块卷积操作将每个阶段的感受野限制在原始大小的四分之一左右。

4.4.7 Would Block Convolution Destroy Useful Features?

块卷积会破坏有用的特征吗？

对于没有块重叠的块卷积，只能保证当前步的所有特征都小于特定粒度，但不能保证所有小于特定粒度的特征都会被保留下来。因此，我们试图在本节中讨论其负面影响和可能的解决方案。我们用两种可能的解决方案进行了消融研究：

• 随机分割，对分割线的位置施加随机抖动（确保相邻步骤之间的区块大小仍然逐渐增大。水平和垂直抖动的间隔分别为 $[0,\frac{w}{4n}]$ 和 $[0,\frac{h}{4n}]$），
• 广泛用于数据增强的随机裁剪。

图片注解：块卷积、随机分割和图像随机裁剪的消融研究

实验以 ResNet50 为基础模型，在 CUB-200-2011 数据集上进行。如表 9 所示，在没有随机分割或随机裁剪的情况下，分块卷积甚至会导致性能下降，这验证了我们的担忧。而当我们在块卷积的基础上单独应用随机分割和随机裁剪时，性能分别提升了 $0.7\%$ 和 $1.5\%$。这两种技术都使每次迭代时分割图像的位置不同，避免了精度下降。此外，当我们同时使用随机分割和随机裁剪时，并没有得到进一步的提高。这很可能是由于随机分割使得相邻两步的块大小相近，而不是稳定的四倍增长，从而削弱了粒度控制对渐进训练的影响。

4.4.8 Would the Learned Multi-Granularity Features Work for Object Across Various Scales?

学习到的多粒度特征是否适用于不同尺度的对象？

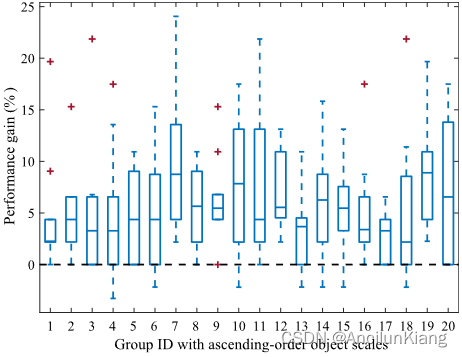
图片注解：在 CUB-200-2011 中，我们的模型与天真 FT-ResNet50 的分类准确率差异说明。CUB-200-2011 中的 200 个鸟类类别按照平均相对比例升序排列，然后平均分成 20 个组。

相对于完整图像的不同物体比例是造成 FGVC 类内差异较大的主要原因之一。因此，有人可能会问，所提出的固定块大小的学习方法是否还能适用于各种物体尺度。对于 CUB-200-2011 中的鸟类来说，它们的尺度主要由其类别决定，例如，就物体尺度而言，鹈鹕一般比麻雀大。因此，为了进一步评估我们的模型在整个数据集中如何处理不同尺度的对象，我们将在本节讨论 CUB-200-2011 中每个类别的性能增益。我们使用 ResNet50 作为骨干网络，FT-ResNet50 作为基线模型。如图 9 所示，CUB-200-2011 中的 200 个鸟类类别按照平均相对比例升序排列，然后平均分成 20 组。在第一组中，鸟类平均只占整幅图像的 $25.3\%$ 左右，而在最后一组中则占 $47.6\%$。我们的方法能始终如一地提升所有 20 个组别，并且不会随着物体尺度的变化而出现任何明显的偏差。

4.5 Visualizations

可视化

4.5.1 Activation Maps of All the Datasets

所有数据集的激活图

图片注解：来自 CUB-200-2011、NA-Birds、Stanford Dogs、Stanford Cars 和 FGVC-Aircraft 数据集的图像的激活图。可视化结果通过以 ResNet50 为骨干网络的 Grad-CAM 算法得出。“低粒度”、"中粒度 "和 "高粒度 "分别指 $Conv(3)$、$Conv(4)$ 和 $Conv(5)$ 处模型注意力的激活图。该图最好以数字方式查看。

如图 4 所示，我们使用 Grad-CAM 算法在五个数据集上生成了我们方法的激活图。我们使用 ResNet50 作为特征提取器，并对其进行了最后三个阶段的渐进式训练。因此，在这里我们将 $Conv(3)$、$Conv(4)$ 和 $Conv(5)$ 的特征图集中可视化，它们分别代表低级粒度、中级粒度和高级粒度的判别部分。明亮区域表示我们的模型重点关注的地方。

可以看出，在每个阶段都有类别标签的监督下，所有阶段的注意力都集中在目标物体上，而忽略了背景噪声。随着网络的深入，网络会首先关注一些局部纹理信息，然后逐渐将注意力转移到更抽象的物体部分。对于 CUB-200-2011 和 NA-birds 中的鸟类，网络在低层阶段主要关注其独特的羽毛和鸟喙，在深层则关注其身体部位。对于 FGVC-Aircraft 数据集中的飞机，网络倾向于在浅层关注其窗户和机轮，这也是合理的，因为有些型号相同但制造年份不同的飞机只能通过计算其窗户的数量来区分。对于大多数图像，其不同阶段的激活图都遵循一个基本规律，即以不同的粒度集中于相同的位置。这表明，多粒度分辨部件的学习是循序渐进的。

4.5.2 Feature Category-Consistency

功能类别–一致性

图片注解：CUB-200-2011 中三种鸟类图像的激活图，供进一步比较。可视化结果通过 Grad-CAM 算法获得，并使用 ResNet50 作为骨干网络。很明显，我们的模型在每个粒度级别上对同一类别中的不同样本都表现出了一致性。对于我们选择的两个相似物种–䴙䴘，模型主要关注它们的颈部，这是区分它们的最重要特征。至于与其他两个物种不相似的 “优雅燕鸥”，模型则倾向于关注它们的羽毛。“低粒度”、"中粒度 "和 "高粒度 "分别指模型在 $Conv(3)$、$Conv(4)$ 和 $Conv(5)$ 处注意力的激活图。该图最好以数字方式查看。

图 5 展示了 CUB-200-2011 数据集中两个相似物种 "Western Grebe "和 "Pied Billed Grebe "的不同样本的可视化结果。可以看出，在每个粒度级别上，同一类别中的所有样本的网络关注度都表现出明显的一致性。对于低粒度部分，模型主要关注鸟类颈部和胸部的一些羽毛纹理。对于中等粒度的部分，模型往往集中在一些身体部位，如鸟类头部或胸部。而对于高细度部分，模型则始终侧重于鸟类的整个上半身。即使鸟类的姿态、光线条件和拍摄角度不同，所提出的模型在面对这些类内差异时也能表现出极大的关注一致性。

此外，当人类区分这两个类别时，"Western Grebe "的颈部包含明显的黑白边界，被认为是可靠的识别标志。因此，在每个粒度级别上，模型的注意力都集中在鸟类的颈部，从而显示出巨大的功效。

4.5.3 Ablation Study of CCBC

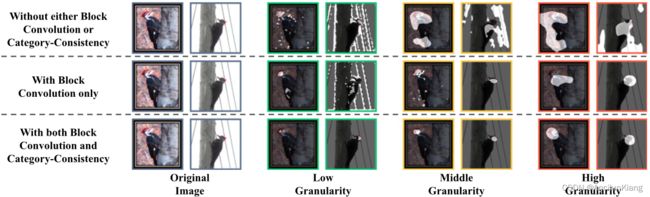
CCBC 消融研究

图片注解：通过模型注意力图的可视化进行消融研究。可视化结果由 Grad-CAM 算法获得，ResNet50 被用作骨干网络。这里我们展示了同一鸟类 "啄木鸟 "的一对图像的激活图，其中有/没有块卷积和类别一致性成分。当移除类别一致性约束时，模型无法聚焦于一致性部分。取消分块卷积操作后，模型无法聚焦于多粒度局部部分。“低粒度”、"中粒度 "和 "高粒度 "分别表示模型在 $Conv(3)$、$Conv(4)$ 和 $Conv(5)$ 处注意力的激活图。该图最好以数字形式显示。

为了进一步证明所提出的 CCBC 各部分（即分块卷积操作和成对类别一致性约束）的有效性，我们对训练时包含/不包含这两个部分的三个不同模型进行了可视化。我们从 CUB-200-2011 数据集中选取了一对属于 "啄木鸟 "的图像，可视化结果如图 7 所示。**有了这两个成分，模型明显集中在这两幅图像中具有一致区分度的局部。**当我们移除类别一致性约束时，模型虽然仍能正确聚焦于目标对象，但却无法定位相同的高粒度部分。而在低粒度级别，模型会受到一些背景噪音的干扰。在此我们推断，**类别一致性约束可以迫使网络挖掘类别中的共同模式，从而提高模型的鲁棒性，防止出现不一致的无意义区域。**当我们用普通卷积层替换块卷积层时，模型不再关注局部部分，也无法挖掘多粒度特征（例如，中粒度层和高粒度层的激活区域显示出相似的粒度）。

4.5.4 Comparison of Jigsaw Patches and The Block Convolution

拼图补丁与区块卷积的比较

图片注解：采用不同粒度控制技术的 CUB-200-2011 数据集中的部分注意力图。为了展示块卷积技术的优越性，我们在可视化过程中使用了洗牌成多粒度拼图的图像作为输入。在每个子图中，第一列列出了输入图像，第二列显示了使用拼图训练的模型的注意力图，第三列显示了使用块卷积训练的模型的注意力图。不同粒度的注意力图是通过相应的网络阶段获得的。“低粒度”、"中粒度 "和 "高粒度 "分别表示模型在 $Conv(3)$、$Conv(4)$ 和 $Conv(5)$ 时的注意力激活图。该图最好以数字方式查看。

为了更好地说明块卷积的优越性，我们将使用拼图和块卷积训练的模型的注意力图可视化。在生成每个阶段的注意力图时，首先将输入图像洗牌成 $n\times n$ 个拼图片段，其中 $n$ 是各训练阶段的超参数集。通过这种方法，我们可以研究两种模型对拼图斑块引入的人为边界的反应。所示图像取自 CUB-200-2011 数据集，ResNet50 用作骨干网络。

如图 8 所示，拼图斑块的负面影响在这些注意力图中得到了清晰的体现，在这些注意力图中，人工边界会引起密集的反应。在每个子图的第二列中，用拼图训练的模型的注意图在低级粒度上显示出明显的网格形状模式，中级粒度的注意图也显示出混乱的分布。相比之下，使用块卷积训练的模型即使在训练过程中从未见过洗牌图像，也能在所有粒度水平上正确定位每个拼图片中具有区分性的部分。可视化结果表明了所提出的分块卷积的优越性，尤其是在使用成对类别一致性约束时。