数据结构:图文详解 树与二叉树(树与二叉树的概念和性质,存储,遍历)
目录
一.树的概念
二.树中重要的概念
三.二叉树的概念
满二叉树
完全二叉树
四.二叉树的性质
五.二叉树的存储
六.二叉树的遍历
前序遍历
中序遍历
后序遍历
一.树的概念
树是一种非线性数据结构,它由节点和边组成。树的每个节点可以有零个或多个子节点,其中一个节点被指定为根节点。树的节点之间通过边连接。另外,树形结构中,子树之间不能有交集,否则就不是树形结构。
树的结构具有层级关系,根节点位于最顶层,而叶节点位于最底层。树的形状可以类比于现实生活中的树,根节点相当于树的根部,而分支和叶子节点则相当于树的枝干和叶子。
在计算机科学中,树被广泛用于各种应用,例如文件系统、数据库索引、编译器中的抽象语法树等。树的常见特点是具有唯一的根节点、没有循环的边、可以有任意数量的子节点等。
树的常见操作包括插入新节点、删除节点、查找节点、遍历节点等。常见的树结构包括二叉树、红黑树、AVL树等。树的设计和使用在算法和数据结构领域中非常重要,它可以提供高效的数据存储和检索方式。
二.树中重要的概念
笔者就以下图作为例子进行说明:
- 结点的度:一个结点含有子树的个数称为该结点的度; 如上图:A的度为6
- 树的度:一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为6
- 叶子结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I...等节点为叶结点
- 双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
- 孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
- 根结点:一棵树中,没有双亲结点的结点;如上图:A
- 结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
- 树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
- 非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G...等节点为分支结点
- 兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
- 堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
- 结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
- 子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
- 森林:由m(m>=0)棵互不相交的树组成的集合称为森林
三.二叉树的概念
二叉树是一种常见的树状数据结构,在二叉树中,每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树的特点是每个节点最多只有两个子节点,且子节点的位置是有序的,即左子节点在右子节点之前。
二叉树可以为空,如果一个二叉树不为空,则它一定由根节点、左子树和右子树组成。每个节点都有一个值,可以是任意类型的数据。
二叉树也可以只有一个节点,如下图所示,根节点不为空,但是左子树和右子树为空,这样的二叉树也是允许存在的
总的来说,对于任意一颗二叉树,它都是由以下几部分复合而成的:
二叉树可以用来表示许多实际问题,例如计算机科学中的排序和搜索算法。在二叉树中,有一些特殊的类型,如满二叉树、完全二叉树和平衡二叉树等。二叉树还可以通过遍历算法来访问其中的节点,最常见的遍历算法有前序遍历、中序遍历和后序遍历。
二叉树中还有以下俩个常见的特殊的二叉树
满二叉树
一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵二叉树的层数为 k ,且结点总数是 ![]() ,则它就是满二叉树。
,则它就是满二叉树。
完全二叉树
完全二叉树是由满二叉树而引出来的,对于深度为 k 的,有 n 个结点的二叉树,当且仅当其每一个结点都与深度为 k 的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树
四.二叉树的性质
- 若规定根结点的层数为1,则一棵非空二叉树的第 i 层上最多有
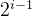 个节点
个节点 - 若规定只有根结点的二叉树的深度为 1 ,则深度为K的二叉树的最大结点数是

- 对任何一棵二叉树, 如果其叶结点个数为 n0 , 度为2的非叶结点个数为 n2 ,则有 n0=n2+1
- 具有 n 个结点的完全二叉树的深度 k 为

- 对于具有 n 个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为 i 的结点有:若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点;若2i+1
五.二叉树的存储
对于任意一个节点,我们最多只能知道它的左右孩子节点和根节点,以及自己保存的数据,由此我们引申出许多种表示二叉树的方法,常见的有孩子表示法,孩子双亲表示法,兄弟节点表示法...
// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}笔者以下图举例:
我们使用孩子表示法,然后依次按照图示组成一颗二叉树(后文的遍历都是基于此树)
public class MyBinaryTree {
public class TreeNode {
public char val;//记录当前节点的值
public TreeNode leftNode;//记录当前节点的左孩子节点
public TreeNode rightNode;//记录当前节点的右孩子节点
public TreeNode(char val) {//初始化节点的值
this.val = val;
}
}
//生成每一个节点,然后连起来
public TreeNode CreatTree() {
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
TreeNode H = new TreeNode('H');
//依次按照图示连起来
A.leftNode = B;
A.rightNode = C;
B.leftNode = D;
C.leftNode = E;
C.rightNode = F;
//最后返回根节点
return A;
}
}六.二叉树的遍历
二叉树的遍历是指按照一定的规则,将二叉树中的所有节点访问一次,并且每个节点只访问一次。常见的二叉树遍历方式有前序遍历、中序遍历和后序遍历。
前序遍历
前序遍历(preorder traversal):先访问根节点,然后遍历左子树,最后遍历右子树。具体步骤如下:
- 访问根节点
- 前序遍历左子树
- 前序遍历右子树
代码实现如下:
//前序遍历
public void preOrder(TreeNode root) {
if (root == null) {
return;//空树不需要遍历
}
System.out.print(root.val + " ");//访问根节点
preOrder(root.leftNode);//前序遍历左子树
preOrder(root.rightNode);//前序遍历右子树
}对于上述的代码,程序运行起来的具体逻辑是如下图这样的,反复的递归和回退进行实现
中序遍历
中序遍历(inorder traversal):先遍历左子树,然后访问根节点,最后遍历右子树。具体步骤如下:
- 中序遍历左子树
- 访问根节点
- 中序遍历右子树
代码实现如下:
//中序遍历
public void inOrder(TreeNode root) {
if (root == null) {
return;//空树不需要遍历
}
inOrder(root.leftNode);//中序遍历左子树
System.out.print(root.val + " ");//访问根节点
inOrder(root.rightNode);//中序遍历右子树
}后序遍历
后序遍历(postorder traversal):先遍历左子树,然后遍历右子树,最后访问根节点。具体步骤如下:
- 后序遍历左子树
- 后序遍历右子树
- 访问根节点
代码实现如下:
//后序遍历
public void postOrder(TreeNode root) {
if (root == null) {
return;//空树不需要遍历
}
postOrder(root.leftNode);//后序遍历左子树
postOrder(root.rightNode);//后序遍历右子树
System.out.print(root.val + " ");//访问根节点
}我们可以写个测试来看看遍历的结果:
public class Test {
public static void main(String[] args) {
MyBinaryTree myBinaryTree = new MyBinaryTree();
MyBinaryTree.TreeNode rootNode = myBinaryTree.CreatTree();
System.out.println();
System.out.println("前序遍历:");
myBinaryTree.preOrder(rootNode);
System.out.println();
System.out.println("中序遍历:");
myBinaryTree.inOrder(rootNode);
System.out.println();
System.out.println("后序遍历:");
myBinaryTree.postOrder(rootNode);
}
}
输出:
也就是说:
其实不管是前序,中序,后序遍历,他们整体的搜索过程都是一样的,不同的地方在于对当前根节点的处理时间不一样:前序遍历是先处理根节点;中序遍历是先遍历当前节点的左子树再处理当前根节点;而后序遍历则是最后再处理根节点,就像下图一样
以上是三种最基本的二叉树遍历方式。除了这三种,还有一些其他的二叉树遍历方式,比如层序遍历、螺旋遍历等。不同的遍历方式适用于不同的场景和问题,可以根据具体的需求选择合适的遍历方式。
![]() 本次的分享就到此为止了,希望我的分享能给您带来帮助,也欢迎大家三连支持,你们的点赞就是博主更新最大的动力!
本次的分享就到此为止了,希望我的分享能给您带来帮助,也欢迎大家三连支持,你们的点赞就是博主更新最大的动力!![]() 如有不同意见,欢迎评论区积极讨论交流,让我们一起学习进步!
如有不同意见,欢迎评论区积极讨论交流,让我们一起学习进步!![]() 有相关问题也可以私信博主,评论区和私信都会认真查看的,我们下次再见
有相关问题也可以私信博主,评论区和私信都会认真查看的,我们下次再见![]()












