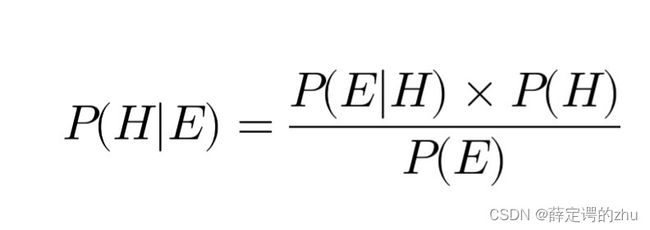贝叶斯定理简介及简单演示

### 贝叶斯定理简介

贝叶斯定理是概率论中的一个核心概念，由18世纪的英国数学家托马斯·贝叶斯提出。该定理提供了一种在已知某些其他概率的情况下，计算某一事件概率的方法。它是基于先验概率和似然概率来计算后验概率。

- **先验概率（Prior Probability）**：在获得新数据之前，我们对某个假设的信念程度。

- **似然概率（Likelihood）**：在已知假设为真的条件下，观察到当前数据的概率。

- **后验概率（Posterior Probability）**：在考虑观察到的数据后，对假设的新信念程度。

定理的数学表达式为：

其中：

•    ( P(H|E) ) 是在事件 E 发生后假设 H 为真的概率（后验概率）。
    •    ( P(E|H) ) 是在假设 H 为真的条件下事件 E 发生的概率（似然概率）。
    •    ( P(H) ) 是假设 H 为真的先验概率。
    •     是事件 E 发生的总概率。

### 贝叶斯算法在处理不确定性和噪声方面的优势

1. **适应性强**：贝叶斯算法能够随着新数据的出现不断更新概率估计，这使其在处理不确定和动态变化的数据时非常有效。

   

2. **整合不同来源的信息**：贝叶斯算法可以融合来自多个源的信息，包括先验知识和新观测数据，使得决策过程更加全面和准确。

3. **鲁棒性**：在数据噪声或缺失情况下，贝叶斯方法因其概率本质，能更好地处理这些不确定性，降低错误决策的风险。

4. **模型的解释性**：贝叶斯模型的输出是概率分布，这不仅可以告诉我们最可能的结果，还可以提供关于这些预测的不确定性的量化估计。

5. **灵活性**：贝叶斯方法可以用于各种统计模型，从简单的线性回归到复杂的神经网络，都可以通过贝叶斯方法来实现和优化。

总的来说，贝叶斯算法在处理实际问题中常见的不确定性和噪声方面展现出显著的优势，尤其适用于需要不断更新数据和信息的动态系统，如室内定位技术。

为了更好地说明贝叶斯算法在室内定位中的应用，我们可以通过一个简化的Java代码示例来展示如何使用贝叶斯定理来更新用户的位置概率。假设我们有一个简单的场景：根据Wi-Fi信号强度来估算用户在两个房间中的位置。

### 示例场景

- 我们有两个房间：房间A和房间B。

- 基于历史数据，我们知道用户有60%的概率在房间A，40%的概率在房间B（先验概率）。

- 当用户的设备接收到Wi-Fi信号时，根据信号强度，我们可以估计用户在房间A的概率为70%，在房间B的概率为30%（似然概率）。

### Java代码示例

public class BayesianIndoorPositioning {

    public static void main(String[] args) {

        // 先验概率

        double priorProbA = 0.6;  // 用户在房间A的先验概率

        double priorProbB = 0.4;  // 用户在房间B的先验概率

        // 似然概率

        double likelihoodA = 0.7; // 在房间A接收到信号的概率

        double likelihoodB = 0.3; // 在房间B接收到信号的概率

        // 计算后验概率

        double postProbA = (likelihoodA * priorProbA) / 

                           (likelihoodA * priorProbA + likelihoodB * priorProbB);

        double postProbB = (likelihoodB * priorProbB) / 

                           (likelihoodA * priorProbA + likelihoodB * priorProbB);

        // 输出结果

        System.out.println("后验概率 用户在房间A的概率: " + postProbA);

        System.out.println("后验概率 用户在房间B的概率: " + postProbB);

    }

}

在这个示例中，我们首先设定了两个房间的先验概率。然后，根据Wi-Fi信号强度计算了用户在每个房间的似然概率。最后，我们使用贝叶斯定理来更新用户在每个房间的后验概率。

### 结果解释

代码运行后会输出用户在房间A和房间B的后验概率。这个概率反映了在考虑了Wi-Fi信号强度之后，用户在每个房间的位置概率。这种方法能够有效地整合先验知识和实时观测数据，提供更准确的定位信息。

请注意，这个示例是为了说明贝叶斯定理在室内定位中的应用而极度简化的。实际应用中，定位算法会更复杂，可能涉及到多个信号源和先进的概率模型。