11.18重启蓝桥杯备赛

 

题目1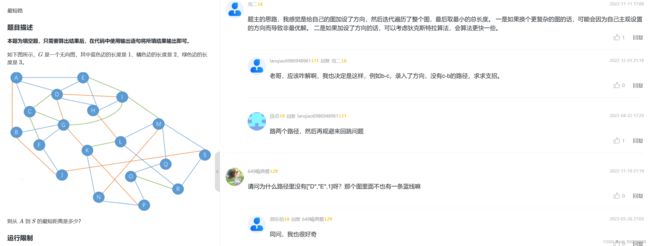

import os
import sys

# 请在此输入您的代码

# 录入路线图
r_list = [
    ["A", "E", 1],
    ["A", "B", 2],
    ["A", "C", 1],
    ["A", "D", 1],
    ["A", "E", 1],
    ["B", "G", 1],
    ["B", "J", 2],
    ["C", "D", 3],
    ["C", "G", 3],
    ["C", "F", 3],
    ["D", "G", 2],
    ["D", "H", 1],
    ["D", "I", 2],
    ["E", "H", 1],
    ["E", "I", 3],
    ["F", "J", 1],
    ["F", "G", 1],
    ["G", "K", 2],
    ["G", "I", 3],
    ["H", "L", 2],
    ["H", "I", 1],
    ["I", "M", 3],
    ["J", "S", 2],
    ["K", "N", 1],
    ["K", "L", 3],
    ["L", "R", 1],
    ["L", "M", 1],
    ["M", "N", 2],
    ["M", "Q", 1],
    ["M", "S", 1],
    ["N", "P", 1],
    ["Q", "O", 1],
    ["O", "R", 3],
    ["P", "O", 1],
    ["R", "S", 1],
]

# 所有路线
nums = []

# 递归
def get(num, r):
    for x, y in enumerate(r_list):

        # 上一个点与当前点一致
        if y[0] == r[1]:

            # 累计长度
            num += y[2]

            # 直到S才结束
            if y[1] == "S":
                nums.append(num)
            # 否则继续
            else:
                get(num=num, r=y)

for q, w in enumerate(r_list):
    n = 0
    # 从A开始
    if w[0] == "A":
        get(num=w[2], r=w)

# 取最小值
print(min(nums))

row = {'A': {'B': 2, 'C': 1, 'D': 1, 'E': 1}, 'B': {'A': 2, 'G': 1, 'J': 2}, 'C': {'A': 1, 'D': 3, 'F': 3, 'G': 3}, 'D': {'A': 1, 'C': 3, 'G': 2, 'H': 1, 'I': 2}, 'E': {'A': 1, 'H': 1, 'I': 3}, 'F': {'C': 3, 'G': 1, 'J': 1}, 'G': {'B': 1, 'C': 3, 'D': 2, 'F': 1, 'I': 3, 'K': 2}, 'H': {'D': 1, 'E': 1, 'I': 1, 'L': 2}, 'I': {'D': 2, 'E': 3, 'G': 3, 'H': 1, 'M': 3}, 'J': {'B': 2, 'F': 1, 'S': 2}, 'K': {'G': 2, 'L': 3, 'N': 1}, 'L': {'H': 2, 'K': 3, 'M': 1, 'R': 1}, 'N': {'K': 1, 'M': 2, 'P': 1}, 'M': {'I': 3, 'L': 1, 'N': 2, 'Q': 1, 'S': 1}, 'O': {'P': 1, 'Q': 1, 'R': 3}, 'P': {'N': 1, 'O': 1}, 'Q': {'M': 1, 'O': 1}, 'R': {'L': 1, 'O': 3, 'S': 1}, 'S':{'J': 2, 'M': 1, 'R': 1}}
book = set()# 已经数过的点
dis = dict((t, 999) for t in row.keys())# 暂存最短距离
#dict.keys返回值为视图对象（view objects）提供了字典实体的动态视图，这就意味着字典改变，视图也会跟着变化
dis['A'] = 0
move_point = 'A'# 正在遍历的点
while len(book) < len(dis):
  book.add(move_point)
  for i in row[move_point]:
    if row[move_point][i] + dis[move_point] < dis[i]:
      dis[i] = row[move_point][i] + dis[move_point]
  next = 999# 在已知点位中找一个最近的点
  for j in row.keys():
    if j not in book and dis[j] < next:
      next = dis[j]
      move_point = j
print(dis['S'])

最短路径之Floyd(弗洛伊德)算法 

简介：
Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

我的上一篇文章讲的dijjstra算法，是图中某一个顶点，到其它顶点之间的最短路径．时间复杂度为O(n2),是单源最短路径

而Floyd算法，是图中每一个顶点，到其它顶点之间的最短路径．时间复杂度为O(n3)．也被称为多源最短路径问题．

算法思想：
１，逐个顶点试探

２，从Ｖi到Vj的所有可能存在的路径中

３，选出一条长度最短的路径

求最短路径步骤：
初始时设置一个n阶方阵，令其对角线元素为0，若存在弧＜Ｖi，Vj＞，则对应元素为权值；否则为∞

逐步试着在原直接路径中增加中间顶点，若加入中间顶点后路径变短，则修改之；否则，维持原值．所有顶点试探完毕，算法结束

实例：

————————————————
版权声明：本文为CSDN博主「any_ways」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/any_ways/article/details/124876432

M=999
network=[
    [0,2,1,1,1,M,M,M,M,M,M,M,M,M,M,M,M,M,M],
    [2,0,M,M,M,M,1,M,M,2,M,M,M,M,M,M,M,M,M],
    [1,M,0,3,M,3,3,M,M,M,M,M,M,M,M,M,M,M,M],
    [1,M,3,0,1,M,2,1,2,M,M,M,M,M,M,M,M,M,M],
    [1,M,M,1,0,M,M,1,3,M,M,M,M,M,M,M,M,M,M],
    [M,M,3,M,M,0,1,M,M,M,M,M,M,M,M,M,M,M,M],
    [M,1,3,2,M,1,0,M,3,M,M,M,M,M,M,M,M,M,M],
    [M,M,M,1,1,M,M,0,1,M,M,2,M,M,M,M,M,M,M],
    [M,M,M,2,3,M,3,1,0,M,M,M,M,M,M,M,M,M,M],
    [M,2,M,M,M,1,M,M,M,0,M,M,M,M,M,M,M,M,2],
    [M,M,M,M,M,M,2,M,M,M,0,3,M,1,M,2,M,M,M],
    [M,M,M,M,M,M,M,2,M,M,3,0,1,M,M,M,M,1,M],
    [M,M,M,M,M,M,M,M,3,M,M,1,0,2,M,M,1,M,1],
    [M,M,M,M,M,M,M,M,M,M,1,M,2,0,M,1,M,M,M],
    [M,M,M,M,M,M,M,M,M,M,M,M,M,M,0,1,1,3,M],
    [M,M,M,M,M,M,M,M,M,M,2,M,M,1,1,0,M,M,M],
    [M,M,M,M,M,M,M,M,M,M,M,M,1,M,1,M,0,M,M],
    [M,M,M,M,M,M,M,M,M,M,M,1,M,M,3,M,M,0,1],
    [M,M,M,M,M,M,M,M,M,2,M,M,1,M,M,M,M,1,0],
]

def Floyd(network):
    n=len(network)
    d=network
#利用三维数组
    for k in range(n):#中间节点
        for i in range(n):
            for j in range(n):
                d[i][j]=min(d[i][j],d[i][k]+d[k][j])
    return d

res=Floyd(network)
print(res[0][18])

题目2 

h = int(input())  # 输入数据
W = [list(map(int, input().split())) for i in range(h)]
#实际是两个list的嵌套
# 循环遍历计算到每一行的和的最大值
for i in range(1, h):
    for j in range(0, i + 1):
        if j == 0:  # 最左边元素只能由右上方得到
            W[i][j] += W[i - 1][j]
        elif j == i:  # 最右边元素只能由左上方得到
            W[i][j] += W[i - 1][j - 1]
        else:  # 其余元素由上方较大值得到
            W[i][j] += max(W[i - 1][j - 1: j + 1]) #下标索引的调用同样是左闭右开
if h & 1:  # 如果是奇数行，则返回最中间值
    print(W[-1][h // 2])
else:  # 偶数行则返回中间较大值
    print(max(W[-1][h // 2 - 1], W[-1][h // 2]))

  & : 按位与操作
(当其数据类型为十进制整型时，需转化为二进制数据进行计算。)
例1：

假设n=6 转化为二进制就是0000 0110,而1的二进制是0000 0001，那么有：

        6=0000 0110

&      1=0000 0001

--------------------------

            0000  0000

由上可知 6 & 1=0

例2：

假设n=5 转化为二进制就是0000 0101,而1的二进制是0000 0001，那么有：

        5=0000 0101

&      1=0000 0001

--------------------------

            0000  0001

由上可知 5 & 1=1

Conclusin:偶数 & 1 = 0（False），奇数 & 1 = 1（True）
————————————————
版权声明：本文为CSDN博主「Toady 元气满满」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/lft_happiness/article/details/126092324

一定要仔细看清题目描述

import os
import sys

# 请在此输入您的代码
n = int(input())        #输入行数n
list_1 = [list(map(int,input().split())) for i in range(n)]       #依次录入数字三角形

list_2 = list_1[:]

for i in range(1,n):                                               #此处i代表循环n-1次 ---->n层中要走n-1步，例如第一层到第二层要走2-1=1步
    for j in range(0,i+1):                                         #此处代表i+1次，------>此处代表列
        if j == 0:                                                 #数字三角形中最左边那个数字只能由右上角哪一个走过来， 即：m[i][j]->m[i-1][j]
            list_2[i][j] = list_1[i][j] + list_1[i-1][j]
        elif j == i:                                               #最右边那一个只能来自左上角。
            list_2[i][j] = list_1[i][j] + list_1[i-1][j-1]
        else:
            list_2[i][j] = list_1[i][j] + max(list_1[i-1][j],list_1[i-1][j-1])

if ((n % 2) == 1):                   #若为奇数，最底层的终点应该是最中间那个，最底层的中间那一个为：list[n][(n%2)+1]
    print(list_2[i][j//2])
if ((n % 2) == 0):                   #若为偶数，最底层的终点为最中间的两个之一，取其中最大的一个就1行了,分别是：list[n][n//2]与list[n][(n//2)+1]
    print(max(list_2[i][n//2-1],list_2[i][n//2]))

妈呀！我竟然能看懂杨辉三角的编程算法了，我好棒！！！ 第三种解法看不懂了，cry

'''
动态规划算法 
状态：dp[i][j]代表到达(i,j)点时的最大和
初始化：dp[0][0]=b[0][0]
状态转移：当j=0时，dp[i][j]=dp[i-1][j]+b[i][j]
当i=j时，dp[i][j]=dp[i-1][j-1]+b[i][j]
否则，dp[i][j]=max(dp[i-1][j-1]+b[i][j],dp[i-1][j]+b[i][j])
当N为奇数时，若要满足向左下走的次数与向右下走的次数相差不超过1，则最后一定走到第N行的最中间的数，即dp[N-1][N//2]
当N为偶数时，若要满足向左下走的次数与向右下走的次数相差不超过1，则最后一定走到第N行的最中间的两个数其中一个，即max(dp[N-1][N//2-1],dp[N-1][N//2])
'''
N=int(input())
b=[]
for i in range(N):
    a=list(map(int,input().split()))
    b.append(a)
dp=[[0 for j in range(i+1)]for i in range(N)]

def dg(dp):
    for i in range(N):
        for j in range(i+1):
            if i==j==0:
                dp[i][j]=b[0][0]
            elif j==0:
                dp[i][j] = dp[i - 1][j] + b[i][j]
            elif i==j:
                dp[i][j] = dp[i - 1][j - 1] + b[i][j]
            else:
                dp[i][j] = max(dp[i - 1][j - 1] + b[i][j], dp[i - 1][j] + b[i][j])
dg(dp)
if (N%2!=0):
    print(dp[N - 1][N // 2])
else:
    print(max(dp[N-1][N//2-1],dp[N-1][N//2]))

Dijkstra算法

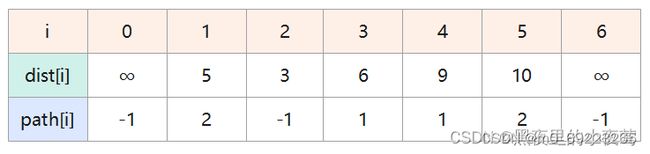
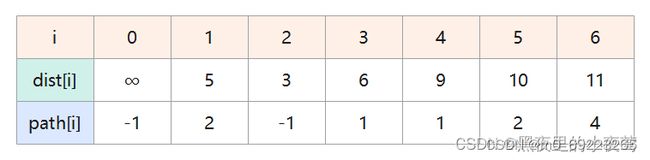
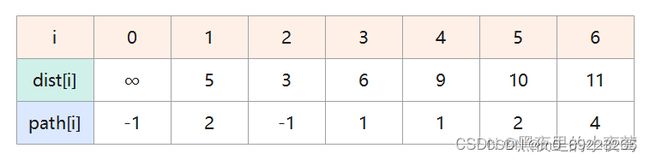
初始化：集合S初始化为{V00}，V00可达V11和V22，其余顶点不可达，因此dist[]数组和path[]数组的设置如下：

第一轮：

第二轮：

第三轮：

第四轮：

第五轮：

第六轮：选出最小值 dist[6]，将顶点 V66 并入集合，此时全部顶点都已包含在S中，结束算法。图算法——求最短路径（Dijkstra算法）_黑夜里的小夜莺的博客-CSDN博客

总结：

Dijkstra算法就是最开始选离源点V0最近的点，然后选好点后，再从选好点的看其邻接点的距离dist[]是否减小，减小就修改dist[]和path[]；

否则就不进行修改操作。

Dijkstra算法基于贪心策略，用邻接矩阵表示图时，来使用Dijkstra算法，

其时间复杂度为O(n*n)。

当边上带有负权值时，Dijkstra算法并不适用。
————————————————
版权声明：本文为CSDN博主「黑夜里的小夜莺」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_61959780/article/details/127983035

 Dijkstra算法的应用

下面的应用Dijkstra算法的程序：

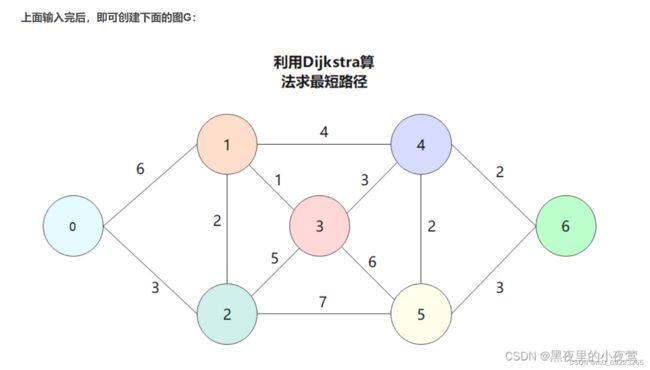
使用此程序需输入以下内容创建图G：

第一步：7 12   #节点数node    路径数path

第二步：0123456   #节点序号

第三步：依次输入下面的内容，输入完一行就按下换行键

0 1 6

0 2 3

1 2 2

1 3 1

1 4 4

2 3 5

2 5 7

3 4 3

3 5 6

4 5 2

4 6 2

5 6 3
————————————————
版权声明：本文为CSDN博主「黑夜里的小夜莺」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_61959780/article/details/127983035