unity 矩阵从模型空间到屏幕空间的转换
这里参考 《unity shader 入门精要》冯乐乐的这本书
深入探索透视投影变换
| 0X01 变换 |
变换这里粗略的讲解下,为了后面的空间转换做铺垫,不是重点,如果看不 明白则看考其他文章
这里讲解的变换有三种:平移变换,缩放变换,旋转变换
说变换就要用到矩阵,这里用4x4矩阵来进行这三种变换
{ M 3 ∗ 3 t 3 ∗ 1 0 1 ∗ 3 1 } (1) \left\{ \begin{matrix} M_{3*3}& t _{3*1} \\ 0_{1*3} & 1 \\ \end{matrix} \right\} \tag{1} {M3∗301∗3t3∗11}(1)
M3*3用于表示旋转和缩放,t3*1用于表示平移,01*3是零矩阵
平移变换
将点(x,y,z)在空间中平移(tx,ty,tz),用矩阵表示为
[ 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ] × [ x y z 1 ] = [ x + t x y + t y z + t z 1 ] (1) \left[ \begin{matrix} 1 & 0&0&t_x \\ 0 & 1&0&t_y \\ 0 & 0&1&t_z \\ 0 & 0&0&1\\ \end{matrix} \right] \times{ \left[ \begin{matrix} x \\y\\z\\1\\ \end{matrix} \right] = \left[ \begin{matrix} x+t_x \\y+t_y\\z+t_z\\1\\ \end{matrix} \right] } \tag{1} ⎣⎢⎢⎡100001000010txtytz1⎦⎥⎥⎤×⎣⎢⎢⎡xyz1⎦⎥⎥⎤=⎣⎢⎢⎡x+txy+tyz+tz1⎦⎥⎥⎤(1)
缩放变换
对模型沿着x轴y轴和z轴进行缩放
[ k x 0 0 0 0 k y 0 0 0 0 k z 0 0 0 0 1 ] × [ x y z 1 ] = [ k x x k y y k z z 1 ] (2) \left[ \begin{matrix} k_x& 0&0&0 \\ 0 & k_y&0&0 \\ 0 & 0&k_z&0 \\ 0 & 0&0&1\\ \end{matrix} \right] \times{ \left[ \begin{matrix} x \\y\\z\\1\\ \end{matrix} \right] = \left[ \begin{matrix} k_xx \\k_yy\\k_zz\\1\\ \end{matrix} \right] } \tag{2} ⎣⎢⎢⎡kx0000ky0000kz00001⎦⎥⎥⎤×⎣⎢⎢⎡xyz1⎦⎥⎥⎤=⎣⎢⎢⎡kxxkyykzz1⎦⎥⎥⎤(2)
旋转变换
这里着重讲下这个,吐槽下好多博客将旋转连旋转正方向都没有说 ,看的云里雾里
关于旋转的正方向,OpenGL与多数图形学书籍规定的正方向为逆时针方向(沿着坐标轴负方向向原点看)

参考这篇文章旋转变换(一)旋转矩阵
绕着z轴旋转 θ \theta θ度的 矩阵
R x ( θ ) = [ c o s ( θ ) − s i n ( θ ) 0 0 s i n ( θ ) c o s ( θ ) 0 0 0 0 1 0 0 0 0 1 ] R_x(\theta) = \left[ \begin{matrix} cos(\theta)&-sin(\theta)&0&0 \\ sin(\theta)&cos(\theta)&0 &0\\ 0& 0&1&0 \\ 0 & 0&0&1\\ \end{matrix} \right] Rx(θ)=⎣⎢⎢⎡cos(θ)sin(θ)00−sin(θ)cos(θ)0000100001⎦⎥⎥⎤
绕着y轴旋转 θ \theta θ度的 矩阵
R x ( θ ) = [ c o s ( θ ) 0 s i n ( θ ) 0 0 1 0 0 − s i n ( θ ) 0 c o s ( θ ) 0 0 0 0 1 ] R_x(\theta) = \left[ \begin{matrix} cos(\theta)&0&sin(\theta)&0\\ 0& 1&0&0 \\ -sin(\theta)&0&cos(\theta)&0 \\ 0 & 0&0&1\\ \end{matrix} \right] Rx(θ)=⎣⎢⎢⎡cos(θ)0−sin(θ)00100sin(θ)0cos(θ)00001⎦⎥⎥⎤
绕着x轴旋转 θ \theta θ度的 矩阵
R x ( θ ) = [ 1 0 0 0 0 c o s ( θ ) − s i n ( θ ) 0 0 s i n ( θ ) c o s ( θ ) 0 0 0 0 1 ] R_x(\theta) = \left[ \begin{matrix} 1& 0&0&0 \\ 0 & cos(\theta)&-sin(\theta)&0 \\ 0 & sin(\theta)&cos(\theta)&0 \\ 0 & 0&0&1\\ \end{matrix} \right] Rx(θ)=⎣⎢⎢⎡10000cos(θ)sin(θ)00−sin(θ)cos(θ)00001⎦⎥⎥⎤
unity中旋转的顺序是首先绕Z轴进行旋转,然后绕X轴进行旋转,最后绕Y轴进行旋转。
| 0X02 坐标空间变换 |
已知子坐标空间C的三个坐标轴在父坐标空间P下的表示xc、yc、zc,以及其原点位置Oc,当给定一个子坐标空间中的点Ac=(a,b,c),求A点用父坐标空间的表示Ap
xc设为(xcx,xcy,xcz),yc设为(ycx,ycy,ycz),zc设为(zcx,zcy,zcz),Oc设为(ocx,ocy,ocz)
这里写结论不写推导过程了
A p = [ x c x y c x z c x o c x x c y y c y z c y o c y x c z y c z z c z o c z 0 0 0 1 ] × [ a b c 1 ] A_p = \left[ \begin{matrix} x_{cx}& y_{cx}& z_{cx}&o_{cx}\\ x_{cy}& y_{cy}& z_{cy}&o_{cy}\\ x_{cz}& y_{cz}& z_{cz}&o_{cz}\\ 0 & 0&0&1\\ \end{matrix} \right] \times{ \left[ \begin{matrix} a \\b\\c\\1\\ \end{matrix} \right] } Ap=⎣⎢⎢⎡xcxxcyxcz0ycxycyycz0zcxzcyzcz0ocxocyocz1⎦⎥⎥⎤×⎣⎢⎢⎡abc1⎦⎥⎥⎤
所以点从子坐标空间到父坐标空间的变换矩阵Mc->p为(|表示是按列展开的)
M c − > p = [ ∣ ∣ ∣ ∣ x c y c z c o c ∣ ∣ ∣ ∣ 0 0 0 1 ] M_{c->p} = \left[ \begin{matrix} |&|&|&|\\ x_{c}& y_{c}& z_{c}&o_{c}\\ |&|&|&|\\ 0 & 0&0&1\\ \end{matrix} \right] Mc−>p=⎣⎢⎢⎡∣xc∣0∣yc∣0∣zc∣0∣oc∣1⎦⎥⎥⎤
矢量(不需要平移)从子坐标空间到父坐标空间的变换矩阵Mc->p为(|表示是按列展开的)
M c − > p = [ ∣ ∣ ∣ x c y c z c ∣ ∣ ∣ ] M_{c->p} = \left[ \begin{matrix} |&|&|\\ x_{c}& y_{c}& z_{c}\\ |&|&|\\ \end{matrix} \right] Mc−>p=⎣⎡∣xc∣∣yc∣∣zc∣⎦⎤
矢量(不需要平移)从父坐标空间到子坐标空间的变换矩阵Mp->c为(-表示是按行展开的)
M p − > c = [ − x c − − y c − − z c − ] M_{p->c} = \left[ \begin{matrix} -& x_{c}&-\\ -& y_{c}& -\\ -& z_{c}&-\\ \end{matrix} \right] Mp−>c=⎣⎡−−−xcyczc−−−⎦⎤
| 0X03 空间变换过程 |
空间变换经历这几个过程:模型空间(model space)—>世界空间(world space)–>观察空间(view space)(右手坐标系)–>裁剪空间(clip space)–>屏幕空间(screen space)
除了观察空间是右手坐标系外其他的全是左手坐标系
屏幕空间 的转换需要经过NDC变换 然后视口坐标变换(只关注x,y;z不关注)再到屏幕坐标
这里用的是 透视 相机没有用正交相机
在文章最下面提供了TransformationMatrixUtil.cs脚本
模型空间到世界空间
根据世界空间对模型空间的平移、旋转、缩放来建立一个变换矩阵,变换矩阵根据上面提到的基础矩阵相乘得到
建立一个 测试脚本TestMatrix.cs 来测试变换坐标
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class TestMatrix : MonoBehaviour {
// Use this for initialization
Camera cam;
/// 场景中配置两个物体 Root,Cube;Root的Transform代表世界空间对Cube模型空间的变换

测试代码的结果:说明变换后的坐标和物体本身世界坐标相同

来看世界空间到模型空间
继续增加测试代码
///
/// 世界空间到模型空间变换对比
/// 这里直接对比变换矩阵是否相同
///
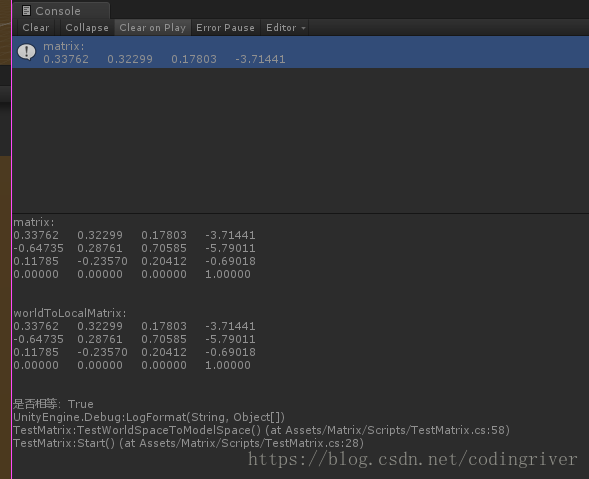
void TestWorldSpaceToModelSpace()
{
//检查世界空间到模型空间
Transform _parent = trans1.parent;
//模型空间转世界空间
Matrix4x4 matrix = TransformationMatrixUtil.MToWMatrix(_parent.localScale, _parent.localEulerAngles, _parent.localPosition);
//世界空间转模型空间;就是matrix的逆矩阵
matrix = matrix.inverse;
Debug.LogFormat("matrix:\n{0}\n\nworldToLocalMatrix:\n{1}\n\n是否相等:{2}", matrix, _parent.worldToLocalMatrix, matrix== _parent.worldToLocalMatrix);
}
模型空间到观察空间
继续增加测试代码
/// 观察空间到裁剪空间
继续增加测试代码
///
/// 测试观察空间到裁剪空间的变换矩阵
///
void TestViewSpaceToClipSpace()
{
//观察空间到裁剪空间矩阵,注意这里是透视相机,没有做正交相机变换矩阵
Matrix4x4 matrix = TransformationMatrixUtil.VToPMatrix();
Debug.LogFormat("matrix:\n{0}\n\n projectionMatrix:\n{1}\n\n是否相等:{2}", matrix, cam.projectionMatrix, matrix == cam.projectionMatrix);
}
模型空间到屏幕空间
这里直接测试从模型空间到世界空间到观察空间到屏幕空间变换
/// 在Start方法中调用后的结果:(如果想要一样的结果则需要设置分辨率为1280*720,并且相机配置一样)
这里只验证屏幕坐标x和y,z值是世界坐标的z值,没有变换的,w值没有研究

脚本TransformationMatrixUtil.cs
//=====================================================
// - FileName: TransformationMatrixUtil.cs
// - Created: wangguoqing
// - UserName: 2018/09/03 17:18:56
// - Email: [email protected]
// - Description:
// - (C) Copyright 2008 - 2015, codingriver,Inc.
// - All Rights Reserved.
//======================================================
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class TransformationMatrixUtil {
/// 测试脚本TestMatrix.cs:
//=====================================================
// - FileName: TestMatrix.cs
// - Created: wangguoqing
// - UserName: 2018/09/03 17:18:56
// - Email: [email protected]
// - Description:
// - (C) Copyright 2008 - 2015, codingriver,Inc.
// - All Rights Reserved.
//======================================================
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
/// github项目
这篇文章整理太麻烦了,前面关于使用矩阵做变换的原理的整理很粗糙,只是为了下面的使用,这篇文章不做过多介绍,之前研究过了,没有记录现在反过头来整理需要仔细理理