ATSS算法
文章目录
- 前言
- ATSS算法的基本原理
- ATSS算法的主要设计步骤
- 算法实现
-
- 伪代码描述如下:
- pytorch
- 分析
-
- 主要优点:
- ATSS算法在一定程度上保证了Tiny Object的阳性样本:
原文
前言
作者比较了FCOS和RetinaNet,发现它们之间主要有三个区别:(1)每个位置平铺锚的数量。RetinaNet在每个位置平铺几个锚盒,而FCOS在每个位置平铺一个锚点。(2)正、负样本的定义。RetinaNet采用IoU,而FCOS则利用空间和尺度约束来选择样本。(3)回归开始状态。RetinaNet从预设锚点回归目标边界框,而FCOS从锚点定位目标。
经过实验发现如果在训练过程中采用相同的正样本和负样本定义,无论是基于锚和无锚检测器,最终的表现都没有明显的差异。也就是说基于锚点和无锚点检测的本质区别在于如何定义正训练样本和负训练样本。
基于此,作者提出了一种自适应样本选择ATSS算法,该算法基于目标特征自动选择正样本和负样本,能够根据GT框和锚框的具体情况动态调整IoU阈值,从而更好地适应各种尺寸和比例的对象,弥合了基于锚点和无锚点检测器之间的差距。
ATSS算法的基本原理
-
候选锚框选取:
- 对于每个Ground Truth(GT)框,计算它与所有候选锚框的IoU(Intersection over Union)。
-
K-最邻近锚框选择:
- 根据预计算的IoU,对每个GT框选择K个IoU最大的锚框作为候选正样本。这些锚框被认为是最有可能包含对象的。
-
计算中心距离和IoU的平均值:
- 对于每个GT框和它的K个候选正样本,分别计算它们中心点之间的距离的平均值(mean distance)和IoU的平均值(mean IoU)。
-
自适应IoU阈值确定:
- 设定一个自适应的IoU阈值τ,该阈值是通过以下公式计算的:
其中α是一个权重参数,通常设置为0.5,表示距离和IoU的影响相等。τ = α * mean_distance + (1 - α) * mean_IoU
- 设定一个自适应的IoU阈值τ,该阈值是通过以下公式计算的:
-
正负样本定义:
- 对于每个GT框和候选锚框,如果它们的IoU大于τ,则将该锚框标记为正样本;否则,标记为负样本。
-
损失函数和训练:
- 使用标记的正负样本进行模型训练,包括分类损失和回归损失。
- 分类损失通常采用交叉熵损失,用于区分背景和前景(即对象)。
- 回归损失通常采用Smooth L1损失,用于调整锚框的位置和大小,使其更接近GT框。
-
推理阶段:
- 在推理阶段,模型会对每个候选锚框生成一个分类分数和一组回归偏移量。
- 通过应用非极大值抑制(NMS)来去除重叠的预测框,并保留最高得分的预测框作为最终的检测结果。
ATSS算法的主要设计步骤
-
预计算IoU:
- 对于每个Ground Truth(GT)框,基于L2距离计算它与所有候选锚框的IoU。
-
计算K个最接近GT框的锚框:
- 根据预计算的IoU,对每个GT框选择K个IoU最大的锚框作为候选正样本。
-
计算中心距离和 IoU 的平均值:
- 对于每个GT框和它的K个候选正样本,计算它们中心点之间的距离的平均值(mean distance)和IoU的平均值(mean IoU)。
-
确定正负样本:
-
设定一个自适应的IoU阈值t,该阈值等于mean distance和mean IoU的加权和,通常权重相等。
-
对于每个GT框和候选锚框,如果它们的IoU大于τ,则将该锚框标记为正样本;否则,标记为负样本。
-
-
训练过程:
-
使用标记的正负样本进行模型训练,计算分类和回归损失。
-
分类损失通常采用交叉熵损失,用于区分背景和前景(即对象)。
-
回归损失通常采用Smooth L1损失,用于调整锚框的位置和大小,使其更接近GT框。
-
-
推理过程:
-
在推理阶段,模型会对每个候选锚框生成一个分类分数和一组回归偏移量。
-
通过应用非极大值抑制(NMS)来去除重叠的预测框,并保留最高得分的预测框作为最终的检测结果。
-
算法实现
伪代码描述如下:
Algorithm 1 Adaptive Training Sample Selection (ATSS)
Input:
G is a set of ground-truth boxes on the image
(G是图像的真值集)
L is the number of feature pyramid levels
(L是特征金字塔的层数)
A i is a set of anchor boxes from the i th pyramid levels
(Ai是金字塔第i层的anchor boxes集)
A is a set of all anchor boxes
(A是所有的锚盒集)
k is a quite robust hyperparameter with a default value of 9
(k是超参数,默认为9)
Output:
P is a set of positive samples
(P是正样本集)
N is a set of negative samples
(N是负样本集)
for each ground-truth g ∈ G do
(对于G集合里的每个真值g)
build an empty set for candidate positive samples of the
ground-truth g: C g ← ∅;
(为g中的候选正样本集建立一个空集Cg)
for each level i ∈ [1,L] do
(对于每一层i)
S i ← select k anchors from A i whose center are closest
to the center of ground-truth g based on L2 distance;
(基于L2距离从Ai中选择离真值g中心最近的k个锚盒)
C g = C g ∪ S i ;
(并入到正样本集Cg中)
end for
compute IoU between C g and g: D g = IoU(C g ,g);
(在Cg和g之间计算IoU:Dg = IoU(Cg,g))
compute mean of D g : m g = Mean(D g );
(计算Dg的均值:mg = Mean(Dg))
compute standard deviation of D g : v g = Std(D g );
(计算Dg的标准差:vg = Std(Dg))
compute IoU threshold for ground-truth g: t g = m g + v g ;
(计算真值g的IoU阈值:tg = mg+vg)
for each candidate c ∈ C g do
(对于每个候选框c∈Cg:)
if IoU(c,g) ≥ t g and center of c in g then
(如果IoU(c,g)≥tg,并且c的中心在g中)
P = P ∪ c;
(则将anchor c添加到阳性样本集P中)
end if
end for
end for
N = A − P;
(负样本集N = 所有的锚盒-正样本anchor)
return P,N;
(返回正负样本集)
pytorch
```python
import torch
import numpy as np
def atss_positive_negative_selection(anchors, gt_boxes, num_samples=9):
"""
ATSS算法的正负样本选择部分
参数:
anchors:形状为(N, 4)的Tensor,表示候选锚框的位置和大小,每个锚框包含(x, y, w, h)
gt_boxes:形状为(M, 4)的Tensor,表示Ground Truth框的位置和大小,每个GT框包含(x, y, w, h)
num_samples:每个GT框选择的候选正样本数量,默认为9
返回:
positive_anchors:形状为(K, 4)的Tensor,表示被标记为正样本的锚框
negative_anchors:形状为(L, 4)的Tensor,表示被标记为负样本的锚框
"""
# 计算IoU
ious = bbox_iou(gt_boxes.unsqueeze(1), anchors.unsqueeze(0))
# 对每个GT框选择K个IoU最大的锚框作为候选正样本
max_ious, argmax_ious = ious.max(dim=1)
topk_args = argmax_ious.argsort(descending=True)[:num_samples]
candidate_anchors = anchors[topk_args]
# 计算中心距离和IoU的平均值
distances = center_distances(candidate_anchors, gt_boxes)
mean_distance = distances.mean(dim=0)
mean_iou = max_ious.mean()
# 自适应地确定IoU阈值
tau = 0.5 * mean_distance + 0.5 * mean_iou
# 根据自适应IoU阈值确定正负样本
ious_with_gt = bbox_iou(gt_boxes.unsqueeze(1), anchors.unsqueeze(0))
is_positive = (ious_with_gt > tau).squeeze(1)
positive_anchors = anchors[is_positive]
negative_anchors = anchors[~is_positive]
return positive_anchors, negative_anchors
def bbox_iou(box1, box2):
"""
计算两个边界框的IoU
参数:
box1, box2:形状分别为(B1, 4)和(B2, 4)的Tensor,表示边界框的位置和大小
返回:
ious:形状为(B1, B2)的Tensor,表示box1和box2之间的IoU
"""
inter_upleft = torch.max(box1[:, :2], box2[:, :2])
inter_botright = torch.min(box1[:, 2:], box2[:, 2:])
inter_wh = torch.clamp(inter_botright - inter_upleft, min=0)
inter_area = inter_wh[:, 0] * inter_wh[:, 1]
area1 = (box1[:, 2] - box1[:, 0]) * (box1[:, 3] - box1[:, 1])
area2 = (box2[:, 2] - box2[:, 0]) * (box2[:, 3] - box2[:, 1])
ious = inter_area / (area1 + area2 - inter_area)
return ious
def center_distances(boxes1, boxes2):
"""
计算两个边界框中心点之间的距离
参数:
boxes1, boxes2:形状分别为(B1, 4)和(B2, 4)的Tensor,表示边界框的位置和大小
返回:
distances:形状为(B1, B2)的Tensor,表示boxes1和boxes2之间中心点的距离
"""
centers1 = (boxes1[:, :2] + boxes1[:, 2:]) / 2
centers2 = (boxes2[:, :2] + boxes2[:, 2:]) / 2
distances = ((centers1[:, None, :] - centers2[None, :, :]) ** 2).sum(dim=-1) ** 0.5
return distances
分析
主要优点:
- 自适应性:ATSS算法通过动态调整IoU阈值来适应各种尺寸和比例的对象,这有助于提高检测精度和泛化能力。
- 简化超参数选择:由于使用了自适应的IoU阈值,ATSS算法减少了对人工设定IoU阈值的依赖,简化了超参数的选择过程。
- 改进的样本定义:通过考虑中心距离和IoU的平均值,ATSS算法能够更准确地定义正负样本,特别是在处理边界情况时。
ATSS算法在一定程度上保证了Tiny Object的阳性样本:
- 动态IoU阈值:ATSS算法根据每个Ground Truth(GT)框和其周围候选锚框的具体情况动态确定IoU阈值。对于微小物体,由于它们的尺寸较小,与候选锚框的中心距离可能会相对较大,这可能导致计算出的自适应IoU阈值较低。较低的IoU阈值使得更多的锚框被标记为正样本,即使它们与微小物体的IoU值相对较低。
- 平衡正负样本:ATSS算法通过考虑中心距离和IoU的平均值来确定自适应IoU阈值,这有助于平衡正负样本的分布。在包含微小物体的场景中,由于微小物体的数量可能较少,这种平衡的样本选择策略有助于确保模型不会过度偏向于背景或较大物体的检测,从而在一定程度上保留了微小物体作为阳性样本的机会。
- K个最邻近锚框:ATSS算法选择每个GT框周围K个IoU最大的候选锚框作为候选正样本。对于微小物体,尽管其尺寸小,但仍有可能有少数锚框与其IoU较高。在选择K个最邻近锚框的过程中,这些与微小物体IoU较高的锚框更有可能被选中,从而提高了微小物体作为阳性样本的可能性。
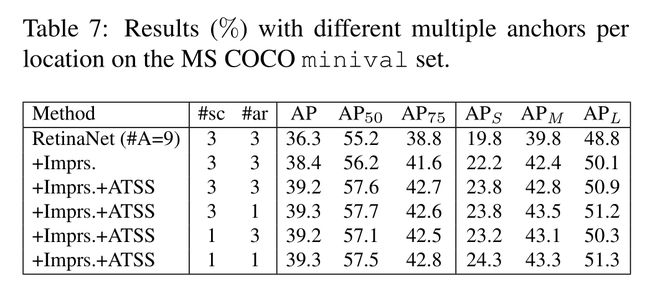
ATSS算法可以轻松集成到现有的基于锚点的目标检测框架中,只需要替换原有的正负样本选择策略即可。如上述提及RetinaNet检测器,采用ATSS算法后,带来了明显的精度提升