Python机器学习入门:从零开始,10天学会
机器学习是人工智能的一个分支,它利用计算机来从数据中学习和做出预测。Python是一种流行的编程语言,它具有强大的科学计算和数据分析功能,非常适合机器学习。
本博客系列将从零开始介绍Python机器学习。我们将从基础知识开始,逐步深入到机器学习的各个方面。通过本系列的学习,您将能够:
-
理解机器学习的基本概念和原理
-
使用Python实现常用的机器学习算法
-
构建自己的机器学习应用
第1天:Python基础
介绍Python语言
Python是一种高级编程语言,具有以下特点:
-
简单易学:Python的语法简洁明了,容易理解和学习。
-
灵活强大:Python具有强大的功能,可以用于各种应用。
-
开源免费:Python是开源软件,可以免费使用和修改。
Python基本语法
Python的基本语法包括:
-
变量:用于存储数据。
-
运算符:用于对数据进行操作。
-
控制流:用于控制程序的执行流程。
-
函数:用于封装代码。
-
模块:用于组织代码。
安装和配置Python环境
要使用Python,首先需要安装Python。Python的安装过程非常简单,可以从Python官方网站下载安装程序进行安装。
安装完成后,还需要配置Python环境。配置Python环境可以通过以下步骤进行:
-
在Windows系统中,打开“控制面板”,选择“系统和安全”,然后选择“系统”。
-
在“系统属性”窗口中,选择“高级系统设置”。
-
在“高级”选项卡中,选择“环境变量”。
-
在“系统变量”中,找到“Path”变量,然后双击打开。
-
在“Path”变量值中,添加Python安装目录下的“Scripts”目录。
配置完成后,就可以开始使用Python了。
练习
以下是一个简单的Python程序:
print("Hello, world!")
这个程序将输出“Hello, world!”。
您可以尝试编写自己的Python程序,来练习Python的基本语法。
第2天:机器学习基础
机器学习的基本概念
机器学习是人工智能的一个分支,它利用计算机来从数据中学习和做出预测。机器学习的目标是让计算机能够从数据中自动学习,并根据这些学习来改进其性能。
机器学习的基本概念包括:
-
数据:机器学习的输入是数据。数据可以是数字、文本、图像或音频等。
-
模型:模型是机器学习的核心。模型是从数据中学习到的规则或函数,用于预测未知数据。
-
学习:机器学习的过程就是学习模型的过程。学习可以通过监督学习、无监督学习或半监督学习等方式进行。
监督学习
监督学习是机器学习中最常见的一种学习方式。在监督学习中,数据被标记为正确或错误。机器学习算法从这些标记的数据中学习,并根据这些学习来预测未知数据。
监督学习的例子包括:
-
分类:将数据划分为多个类别。例如,将图片分类为猫狗。
-
回归:预测数值型数据。例如,预测房价。
无监督学习
无监督学习是机器学习的另一种常见的学习方式。在无监督学习中,数据没有被标记为正确或错误。机器学习算法从这些未标记的数据中学习,并根据这些学习来发现数据中的模式或结构。
无监督学习的例子包括:
-
聚类:将数据划分为具有相似特征的组。例如,将客户划分为不同类型的客户。
-
降维:将高维数据降维到低维数据。例如,将图像降维到二维或三维。
半监督学习
半监督学习是介于监督学习和无监督学习之间的一种学习方式。在半监督学习中,数据既有标记的数据,也有未标记的数据。机器学习算法从这些数据中学习,并根据这些学习来预测未知数据。
半监督学习的例子包括:
-
异常检测:识别异常数据。例如,识别信用卡欺诈。
-
推荐系统:推荐用户感兴趣的产品或服务。
机器学习的应用
机器学习已经在各个领域得到了广泛的应用,包括:
-
自然语言处理:处理和理解人类语言。
-
计算机视觉:处理和理解图像和视频。
-
语音识别:识别和理解人类的语音。
-
推荐系统:推荐用户感兴趣的产品或服务。
-
金融:预测市场趋势、识别欺诈等。
-
医疗:诊断疾病、开发新药等。
结论
机器学习是一门快速发展的技术,具有广阔的应用前景。通过学习机器学习的基本概念和原理,您将能够理解机器学习的应用,并利用机器学习来解决实际问题。
第3天:数据预处理
数据预处理的重要性
数据预处理是机器学习中的重要环节,它可以确保数据的质量,提高机器学习模型的性能。
数据预处理的重要性主要体现在以下几个方面:
-
提高数据的质量:数据预处理可以清除数据中的噪声,填补缺失值,统一数据格式等,从而提高数据的质量。
-
提高模型的鲁棒性:数据预处理可以减少数据中的异常值,从而提高模型的鲁棒性。
-
提高模型的泛化能力:数据预处理可以使数据更加符合模型的假设,从而提高模型的泛化能力。
数据预处理的基本方法
数据预处理的基本方法包括:
-
数据清洗:数据清洗是数据预处理的第一步,它包括去除噪声、填补缺失值等。
-
数据转换:数据转换是将数据转换为机器学习算法可以处理的格式,包括数据格式转换、数据归一化等。
-
数据降维:数据降维是将高维数据降维到低维数据,从而提高模型的计算效率和泛化能力。
数据预处理的常见问题
在数据预处理过程中,可能会遇到以下一些问题:
-
数据选择:如何选择合适的数据进行预处理?
-
数据特征选择:如何选择合适的特征进行预处理?
-
数据预处理的效果评估:如何评估数据预处理的效果?
结论
数据预处理是机器学习中的重要环节,它可以确保数据的质量,提高机器学习模型的性能。在进行数据预处理时,需要注意选择合适的数据和特征,并评估数据预处理的效果。
第4天:线性回归
线性回归的基本概念
线性回归是一种监督学习算法,它用于预测数值型数据。线性回归假设因变量与自变量之间存在线性关系,即:
y = ax + b
其中,y 是因变量,x 是自变量,a 和 b 是模型参数。
线性回归的目标是通过学习数据,找到 a 和 b 的值,使模型能够尽可能准确地预测未知数据。
线性回归的实现方法
线性回归可以通过以下两种方法实现:
最小二乘法
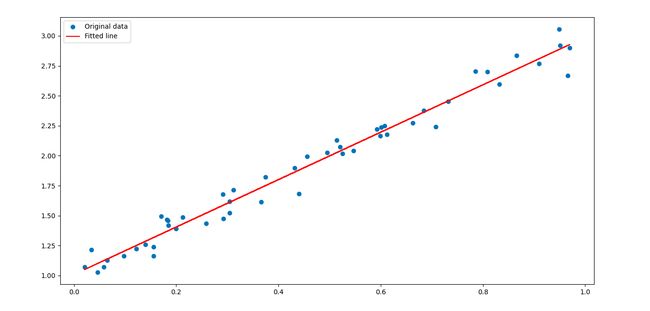
最小二乘法是一种用于拟合数据和估计模型参数的常见方法。在Python中,你可以使用NumPy库来进行最小二乘法的实现。以下是一个简单的例子,演示如何使用最小二乘法拟合一条直线(如下图所示):
import numpy as np
import matplotlib.pyplot as plt
# 生成一些示例数据
np.random.seed(42)
x = np.random.rand(50)
y = 2 * x + 1 + 0.1 * np.random.randn(50)
# 使用最小二乘法拟合直线 y = mx + b
A = np.vstack([x, np.ones(len(x))]).T
m, b = np.linalg.lstsq(A, y, rcond=None)[0]
# 绘制原始数据和拟合直线
plt.scatter(x, y, label='Original data')
plt.plot(x, m * x + b, 'r', label='Fitted line')
plt.legend()
plt.show()在这个例子中,numpy.linalg.lstsq 函数被用于执行最小二乘法。A 是一个包含两列的矩阵,其中第一列是输入数据 x,第二列是常数项 1。拟合的直线参数存储在 m 和 b 中。
梯度下降法
梯度下降法是一种优化算法,用于最小化(或最大化)一个目标函数。下面是一个简单的 Python 示例,演示如何使用梯度下降法来拟合线性回归模型:
import numpy as np
import matplotlib.pyplot as plt
# 生成一些示例数据
np.random.seed(42)
x = np.random.rand(50)
y = 2 * x + 1 + 0.1 * np.random.randn(50)
# 定义线性回归模型
def linear_regression(x, theta0, theta1):
return theta0 + theta1 * x
# 定义损失函数(均方误差)
def mean_squared_error(y_true, y_pred):
return np.mean((y_true - y_pred) ** 2)
# 定义梯度下降函数
def gradient_descent(x, y, theta0, theta1, learning_rate, epochs):
m = len(x)
for epoch in range(epochs):
# 计算预测值
y_pred = linear_regression(x, theta0, theta1)
# 计算梯度
gradient_theta0 = -2 * np.sum(y - y_pred) / m
gradient_theta1 = -2 * np.sum((y - y_pred) * x) / m
# 更新参数
theta0 -= learning_rate * gradient_theta0
theta1 -= learning_rate * gradient_theta1
# 计算损失并输出
loss = mean_squared_error(y, y_pred)
if epoch % 100 == 0:
print(f'Epoch {epoch}, Loss: {loss}')
return theta0, theta1
# 初始化参数
theta0_initial = 0
theta1_initial = 0
learning_rate = 0.1
epochs = 1000
# 运行梯度下降算法
theta0, theta1 = gradient_descent(x, y, theta0_initial, theta1_initial, learning_rate, epochs)
# 绘制原始数据和拟合直线
plt.scatter(x, y, label='Original data')
plt.plot(x, linear_regression(x, theta0, theta1), 'r', label='Fitted line')
plt.legend()
plt.show()在这个例子中,我们通过定义一个线性回归模型和均方误差损失函数来实现梯度下降。然后,我们使用梯度下降算法更新模型参数 theta0 和 theta1,并在每个迭代中计算损失。最后,我们绘制原始数据和拟合直线。(下图是每次迭代后计算的损失)
线性回归的应用
线性回归在各个领域都有广泛的应用,包括:
预测房价
通过线性回归,可以确定对房价有显著影响的特征。这些特征可以包括房屋的大小、地理位置、房龄、卧室数量等。可以利用新的房屋特征数据输入模型,从而预测相应房屋的价格。这对于买卖双方、投资者和房地产开发商等都具有重要的参考价值。
预测销量
线性回归在销量预测中的应用场景有很多,比如:
-
市场营销: 通过分析广告投入、促销活动、市场份额等因素与销售之间的线性关系,企业可以利用线性回归模型来预测未来销售趋势,优化市场营销策略。
-
库存管理: 分析历史销售数据,识别销售量与时间、季节性等因素的关系,从而帮助企业更好地管理库存水平,减少库存成本。
-
定价策略: 了解产品定价与销售数量之间的关系,从而制定更具竞争力的定价策略,平衡销售数量和利润。
-
供应链规划: 规划供应链,确保产品的生产和配送能够满足市场需求,同时避免过多的库存积压。
-
新产品上市: 在新产品上市前,通过线性回归分析类似产品的销售数据,可以预测新产品的潜在销售表现,有助于优化生产计划和市场推广策略。
预测客户满意度
通过线性回归,可以分析各种与顾客满意度相关的因素,比如:服务质量分析、产品特征、产品价格、市场活动、员工表现。
结论
线性回归是一种简单易用的监督学习算法,它可以用于预测数值型数据。通过学习线性回归,您将能够理解线性回归的基本概念和原理,并能够实现线性回归模型。
第5天:逻辑回归
逻辑回归的基本概念
逻辑回归是一种监督学习算法,它用于二分类问题。逻辑回归假设因变量与自变量之间存在线性关系,但输出值是概率,即:
P(y=1|x) = g(ax+b)
其中,y 是因变量,x 是自变量,a 和 b 是模型参数,g 是激活函数。
逻辑回归的目标是通过学习数据,找到 a 和 b 的值,使模型能够尽可能准确地预测未知数据的类别。
逻辑回归的实现方法
逻辑回归可以通过以下两种方法实现:
最大似然估计
最大似然估计(Maximum Likelihood Estimation,简称MLE)是一种用于估计统计模型参数的方法。在 Python 中,你可以使用 SciPy 库来进行最大似然估计。以下是一个简单的例子,演示如何使用最大似然估计来拟合正态分布的参数:
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
from scipy.optimize import minimize
# 生成一些正态分布的示例数据
np.random.seed(42)
data = np.random.normal(loc=2, scale=1.5, size=1000)
# 定义负对数似然函数(用于最小化)
def negative_log_likelihood(params, data):
mean, std_dev = params
log_likelihood = np.sum(norm.logpdf(data, loc=mean, scale=std_dev))
return -log_likelihood
# 初始参数猜测
initial_guess = [1, 1]
# 最大似然估计
result = minimize(negative_log_likelihood, initial_guess, args=(data,))
mean_mle, std_dev_mle = result.x
# 输出估计的参数
print(f'Mean MLE: {mean_mle}')
print(f'Standard Deviation MLE: {std_dev_mle}')
# 绘制直方图和拟合的正态分布
plt.hist(data, bins=30, density=True, alpha=0.6, color='g', label='Histogram')
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, mean_mle, std_dev_mle)
plt.plot(x, p, 'k', linewidth=2, label='Fitted distribution')
plt.title('Fit results: Mean = %.2f, Standard Deviation = %.2f' % (mean_mle, std_dev_mle))
plt.legend()
plt.show()在这个例子中,我们首先生成一些正态分布的示例数据。然后,我们定义了一个负对数似然函数,该函数用于最小化。接着,我们使用 SciPy 中的 minimize 函数进行最大似然估计,找到使得负对数似然最小的参数值。最后,我们输出估计的均值和标准差,并绘制直方图以及拟合的正态分布。
逻辑回归的应用
逻辑回归在各个领域都有广泛的应用,包括:
垃圾邮件过滤
逻辑回归是一种二分类算法,主要用于处理输出为两个类别的问题。在垃圾邮件过滤中,通常将问题建模为二分类问题,其中两个类别分别是“垃圾邮件”和“非垃圾邮件”(正常邮件)。
基本工作原理是在垃圾邮件中提取特征,这些特征可以包括邮件中的关键词、文本内容的特殊符号、邮件发送者的信誉等,通过学习训练数据中的特征权重,建立一个分类模型,模型输出的概率可以通过设置阈值来判断邮件是否为垃圾邮件。
客户流失预测
逻辑回归可以用于分析客户特征(例如购买频率、投诉次数、使用时长等)与流失之间的关系。通过大量的数据训练建立一个分类模型,这个模型可以用于未来的新客户,帮助预测他们是否可能流失。
信用卡欺诈检测
信用卡欺诈检测是金融领域中的重要问题之一,而逻辑回归可以用于建立欺诈与非欺诈之间的分类模型。历史数据主要是通过分析信用卡交易数据中各种特征(如交易金额、交易地点、交易时间等)与欺诈之间的关系建立分类模型。通过该模型来识别异常交易。
结论
逻辑回归是一种简单易用的监督学习算法,它可以用于二分类问题。通过学习逻辑回归,您将能够理解逻辑回归的基本概念和原理,并能够实现逻辑回归模型。
第6天:K-均值聚类
K-均值聚类的基本概念
K-均值聚类是一种无监督学习算法,它用于将数据划分为具有相似特征的 K 个簇。K-均值聚类假设每个簇的中心是固定的,即:
C_k = {x \in X | ||x - \mu_k||^2 \le ||x - \mu_j||^2, \forall j \ne k}
其中,C_k 是第 k 个簇,X 是数据集,\mu_k 是第 k 个簇的中心,|| . || 是欧式距离。
K-均值聚类的目标是通过迭代的方式,找到使得簇内距离最小、簇间距离最大 K 个簇。
K-均值聚类的实现方法
K-均值聚类可以通过以下步骤实现:
-
初始化 K 个质心。
-
将每个数据点分配到距离其最近的质心所在的簇。
-
更新每个簇的中心。
-
重复步骤 2 和 3,直到簇的中心不再发生变化。
在 Python 中,你可以使用 scikit-learn 库来实现 K-均值聚类。以下是一个简单的例子:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# 生成一些示例数据
data, labels = make_blobs(n_samples=300, centers=4, random_state=42)
# 使用KMeans算法聚类
kmeans = KMeans(n_clusters=4, random_state=42)
kmeans.fit(data)
centroids = kmeans.cluster_centers_
labels_pred = kmeans.labels_
# 绘制聚类结果和质心
plt.scatter(data[:, 0], data[:, 1], c=labels_pred, cmap='viridis', alpha=0.7, edgecolors='k')
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='X', s=200, label='Centroids')
plt.title('K-Means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()在这个例子中,我们首先使用 make_blobs 函数生成一些带有标签的示例数据。然后,我们使用 KMeans 类来进行 K-均值聚类,指定簇的数量为 4。最后,我们绘制聚类结果和质心。
K-均值聚类的应用
K-均值聚类在各个领域都有广泛的应用,包括:
图像分割
在图像分割领域,K均值聚类可以被广泛应用,比如:
-
颜色分割: K均值聚类可用于将图像中的像素按颜色分成不同的簇。这对于分离不同对象或区域的颜色是有用的,例如在医学图像处理中分割组织或细胞。
-
纹理分割: 当图像中存在不同纹理的区域时,K均值聚类可以用于将相似纹理的像素分成同一簇,从而实现纹理分割。
-
物体识别: 在目标检测和物体识别任务中,K均值聚类可以帮助将图像分割成包含不同物体的区域,有助于进一步的分析和识别。
-
图像预处理: K均值聚类可以作为图像预处理步骤,帮助简化图像结构并减少数据维度,从而提高后续图像分析任务的效率。
-
图像分割初步步骤: 在一些情况下,K均值聚类可以作为图像分割的初始步骤,然后更复杂的分割算法可以在其基础上进一步细化分割结果。
文本聚类
在文本聚类中,常常使用词袋模型或词嵌入等表示文本特征的方法,并将这些特征输入K-均值聚类算法中进行分组。
以下是K-均值聚类在文本聚类中的一些应用场景:
-
新闻聚类: K-均值聚类可用于对大量新闻文章进行聚类,将相似主题或话题的文章分组在一起,以便更好地组织和浏览新闻内容。
-
社交媒体分析: 在社交媒体数据中,K-均值聚类可以用于将相似的社交媒体帖子或评论聚集在一起,以揭示用户的兴趣、情感或讨论话题。
-
文档组织: 对于大型文档集合,K-均值聚类可以用于将文档组织成具有相似主题的簇,方便用户查找和检索相关信息。
-
信息检索: 在信息检索中,K-均值聚类可用于组织和分组检索到的文档,以提供更有结构的检索结果。
-
用户评论分析: 对于包含大量用户评论的产品或服务,K-均值聚类可用于将具有相似观点或情感的评论聚集在一起,从而了解用户反馈。
-
主题建模: K-均值聚类可以用于构建主题模型,将文本数据分解为多个主题簇,有助于理解文本数据的结构和内容。
客户分类
客户分类是将客户划分为不同的群体,使得同一组内的客户具有相似的特征,这有助于企业更好地了解其客户群体、提供个性化服务以及制定更有针对性的营销策略。
以下是K均值聚类在客户分类中的一些应用场景:
-
消费行为分析: 通过K均值聚类,企业可以将客户根据其购买行为划分为不同的群体。例如,一些客户可能更倾向于购买高端产品,而另一些客户可能更注重折扣和促销。
-
市场细分: K均值聚类可用于对市场进行细分,将整个市场分成具有相似需求和行为的子市场。这有助于企业更有针对性地推出产品和服务。
-
客户满意度分析: 通过K均值聚类,可以将客户按照对服务满意度的评价划分为不同的群体。这有助于企业更好地理解不同群体客户的需求和偏好,改进服务质量。
-
营销策略制定: 将客户分成不同的群体后,企业可以根据每个群体的特征制定个性化的营销策略。这可以提高营销效果,因为不同群体的客户对于不同的推广方式和产品定价可能有不同的反应。
-
客户维护和忠诚度: 通过K均值聚类,企业可以识别出哪些客户属于高价值客户、潜在流失客户等。根据这些分类,可以采取有针对性的客户维护措施,提高客户满意度和忠诚度。
结论
K-均值聚类是一种简单易用的无监督学习算法,它可以用于将数据划分为具有相似特征的 K 个簇。通过学习 K-均值聚类,您将能够理解 K-均值聚类的基本概念和原理,并能够实现 K-均值聚类模型。
第7天:决策树
决策树的基本概念
决策树是一种监督学习算法,它用于分类和回归问题。决策树是一种树形结构,每个节点都代表一个决策,每个分支都代表一个可能的结果。
决策树的目标是通过学习数据,构建一棵能够对未知数据进行正确分类或预测的决策树。
决策树的实现方法
决策树可以通过以下两种方法实现:
ID3 算法
ID3(Iterative Dichotomiser 3)算法是一种用于构建决策树的算法,它采用迭代的方式递归地将数据集分割成更小的子集。在 Python 中,你可以使用递归方法实现 ID3 算法。以下是一个简单的示例:
import numpy as np
class Node:
def __init__(self, feature=None, value=None, result=None):
self.feature = feature # 用于划分的特征
self.value = value # 划分的值
self.result = result # 叶节点的输出结果
self.children = {} # 子节点
def entropy(y):
_, counts = np.unique(y, return_counts=True)
probabilities = counts / len(y)
return -np.sum(probabilities * np.log2(probabilities))
def information_gain(X, y, feature, value):
mask = X[:, feature] <= value
left_entropy = entropy(y[mask])
right_entropy = entropy(y[~mask])
total_entropy = entropy(y)
return total_entropy - (len(y[mask]) / len(y) * left_entropy + len(y[~mask]) / len(y) * right_entropy)
def find_best_split(X, y):
best_feature = None
best_value = None
best_info_gain = -1
for feature in range(X.shape[1]):
unique_values = np.unique(X[:, feature])
for value in unique_values:
info_gain = information_gain(X, y, feature, value)
if info_gain > best_info_gain:
best_info_gain = info_gain
best_feature = feature
best_value = value
return best_feature, best_value
def build_tree(X, y):
if len(np.unique(y)) == 1: # 如果所有样本属于同一类别,创建叶节点
return Node(result=y[0])
best_feature, best_value = find_best_split(X, y)
if best_feature is None: # 如果无法继续划分,创建叶节点
return Node(result=np.argmax(np.bincount(y)))
node = Node(feature=best_feature, value=best_value)
mask = X[:, best_feature] <= best_value
node.children['left'] = build_tree(X[mask], y[mask])
node.children['right'] = build_tree(X[~mask], y[~mask])
return node
def predict_sample(tree, sample):
if tree.result is not None: # 如果是叶节点,返回结果
return tree.result
if sample[tree.feature] <= tree.value:
return predict_sample(tree.children['left'], sample)
else:
return predict_sample(tree.children['right'], sample)
def predict(tree, X):
return np.array([predict_sample(tree, sample) for sample in X])
# 生成一些示例数据
X = np.array([[1, 2],
[2, 3],
[3, 4],
[4, 5],
[5, 6]])
y = np.array([0, 0, 1, 1, 1])
# 构建决策树
tree = build_tree(X, y)
# 预测新样本
new_samples = np.array([[2, 3], [4, 5]])
predictions = predict(tree, new_samples)
print("Predictions:", predictions)
# 打印结果
# Predictions: [0 1]在这个示例中,我们定义了 Node 类来表示决策树的节点。entropy 函数计算信息熵,information_gain 函数计算信息增益,find_best_split 函数找到最佳划分点,build_tree 函数递归地构建决策树,而 predict 函数用于预测新的样本。
C4.5 算法
C4.5 算法是 ID3 算法的改进版本。C4.5 算法通过计算信息增益比来选择划分数据的属性。
以下是一个简化的 Python 示例,演示了C4.5算法的基本原理。
import numpy as np
### 定义一些基本的数据结构和计算函数
class TreeNode:
def __init__(self, feature=None, value=None, result=None, children=None):
self.feature = feature # 用于划分的特征
self.value = value # 划分的值(对于离散特征)或者 None(对于连续特征)
self.result = result # 叶节点的输出结果
self.children = children or {} # 子节点
def entropy(y):
_, counts = np.unique(y, return_counts=True)
probabilities = counts / len(y)
return -np.sum(probabilities * np.log2(probabilities + 1e-10))
def information_gain(X, y, feature, value):
mask = X[:, feature] == value
left_entropy = entropy(y[mask])
right_entropy = entropy(y[~mask])
total_entropy = entropy(y)
return total_entropy - (len(y[mask]) / len(y) * left_entropy + len(y[~mask]) / len(y) * right_entropy)
def find_best_split(X, y, features, used_features=[]):
best_feature = None
best_value = None
best_info_gain = -1
for feature in features:
if feature in used_features:
continue
unique_values = np.unique(X[:, feature])
for value in unique_values:
info_gain = information_gain(X, y, feature, value)
if info_gain > best_info_gain:
best_info_gain = info_gain
best_feature = feature
best_value = value
return best_feature, best_value
def majority_vote(y):
unique_values, counts = np.unique(y, return_counts=True)
return unique_values[np.argmax(counts)]
def split_data(X, y, feature, value):
mask = X[:, feature] == value
return X[mask], y[mask], X[~mask], y[~mask]
### 主体部分
def build_tree(X, y, features, used_features=[]):
if len(np.unique(y)) == 1: # 如果所有样本属于同一类别,创建叶节点
return TreeNode(result=y[0])
best_feature, best_value = find_best_split(X, y, features, used_features)
if best_feature is None: # 如果无法继续划分,创建叶节点
return TreeNode(result=majority_vote(y))
used_features.append(best_feature)
node = TreeNode(feature=best_feature, value=best_value)
if best_value is not None: # 处理离散特征
unique_values = np.unique(X[:, best_feature])
for value in unique_values:
sub_X, sub_y, _, _ = split_data(X, y, best_feature, value)
node.children[value] = build_tree(sub_X, sub_y, features, used_features)
else: # 处理连续特征
sub_X1, sub_y1, sub_X2, sub_y2 = split_data(X, y, best_feature, best_value)
node.children['<='] = build_tree(sub_X1, sub_y1, features, used_features)
node.children['>'] = build_tree(sub_X2, sub_y2, features, used_features)
return node
def predict_sample(tree, sample):
if tree.result is not None: # 如果是叶节点,返回结果
return tree.result
if tree.value is not None: # 处理离散特征
return predict_sample(tree.children[sample[tree.feature]], sample)
else: # 处理连续特征
if sample[tree.feature] <= tree.value:
return predict_sample(tree.children['<='], sample)
else:
return predict_sample(tree.children['>'], sample)
def predict(tree, X):
return np.array([predict_sample(tree, sample) for sample in X])
### 使用示例数据并构建C4.5决策树
# 生成一些示例数据
X = np.array([
[1, 'S'],
[1, 'M'],
[1, 'M'],
[1, 'S'],
[1, 'S'],
[2, 'S'],
[2, 'M'],
[2, 'M'],
[2, 'L'],
[2, 'L'],
[3, 'L'],
[3, 'M'],
[3, 'M'],
[3, 'L'],
[3, 'L']
])
y = np.array(['N', 'N', 'Y', 'Y', 'Y', 'N', 'N', 'Y', 'Y', 'Y', 'Y', 'Y', 'Y', 'Y', 'N'])
# 特征:0表示数字特征,1表示离散特征
features = [0, 1]
# 构建C4.5决策树
tree = build_tree(X, y, features)
# 预测新样本
new_samples = np.array([[2, 'S'], [3, 'M']])
predictions = predict(tree, new_samples)
print("Predictions:", predictions)
# 输出打印结果
# Predictions: ['N' 'Y']决策树的应用
决策树在各个领域都有广泛的应用,包括:
信用卡欺诈检测
基于决策树模型的训练,可以对实时的信用卡交易进行预测和分类。这有助于快速识别潜在的欺诈行为,并及时采取防范措施。
疾病诊断
决策树可以用于帮助医生做出诊断决策、指导治疗方案或者预测患者的疾病风险。
决策树模型可以根据患者的症状、检查结果等特征对患者进行疾病分类。这有助于医生更准确地判断患者的疾病类型,推荐最适合的治疗策略。但是,医学领域的决策树应用需要经过充分的验证和临床试验,确保其在真实临床环境中的有效性和安全性。
推荐系统
推荐系统是利用用户的历史行为、兴趣和其他信息,为用户提供个性化推荐的系统。决策树可以用于建模用户与物品(如商品、电影、音乐等)之间的关系,从而实现个性化的推荐。
以下是决策树在推荐系统中的一些应用场景:
-
特征选择: 决策树可以用于选择用户和物品特征中最为关键的因素。这有助于确定在推荐系统中需要考虑哪些因素,如用户的历史行为、偏好、社交网络关系等。
-
用户兴趣建模: 决策树可以用于建模用户的兴趣。通过分析用户与不同物品之间的关系,决策树可以预测用户对未来物品的兴趣,从而实现个性化推荐。
-
物品推荐: 基于用户的历史行为和特征,决策树可以帮助确定哪些物品最有可能被用户喜欢。这有助于系统向用户推荐他们可能感兴趣的物品。
-
冷启动问题: 决策树在解决推荐系统中的冷启动问题(对新用户或新物品的推荐)时可以发挥作用。通过分析用户和物品的特征,决策树可以为新用户或新物品做出初步的推荐。
-
解释性和可解释性: 决策树是一种可解释性较强的模型,可以提供推荐的决策路径,有助于理解为什么给用户推荐了某个物品。
结论
决策树是一种简单易用的监督学习算法,它可以用于分类和回归问题。通过学习决策树,您将能够理解决策树的基本概念和原理,并能够实现决策树模型。
决策树的优缺点
优点
-
易于理解和解释。
-
可以处理多分类问题。
-
可以处理连续型和离散型数据。
缺点
-
容易过拟合。
-
对数据的噪声敏感。
决策树的优化
为了解决决策树的过拟合问题,可以采用以下方法:
-
剪枝:在决策树生成后,可以通过剪枝来去除一些不重要的节点,从而减少过拟合。
-
正则化:在决策树训练时,可以加入正则化项,从而减少模型的复杂度,从而减少过拟合。
-
使用集成学习:可以将多个决策树进行集成,从而减少过拟合。
第8天:支持向量机
支持向量机的基本概念
支持向量机(Support Vector Machine,SVM)是一种监督学习算法,它用于分类和回归问题。SVM 的基本模型是在特征空间上找到一个最大边距的超平面,使得训练数据的两类数据被超平面正确分割。
支持向量机的实现方法
支持向量机可以通过以下两种方法实现:
SMO 算法
实现SMO(Sequential Minimal Optimization)算法是一个相对复杂的任务,因为它涉及到对支持向量机的训练过程进行优化。SMO算法的主要目标是通过迭代优化一对拉格朗日乘子,以达到支持向量机的最优解。以下是一个简化版的 Python 代码示例,实现了基本的SMO算法,但请注意这只是一个基本的参考,真正的SMO算法实现可能会更加复杂和优化:
import numpy as np
class SVM:
def __init__(self, X, y, C, tol, max_iter, kernel):
self.X = X
self.y = y
self.C = C
self.tol = tol
self.max_iter = max_iter
self.kernel = kernel
self.m, self.n = X.shape
# 初始化拉格朗日乘子和偏置项
self.alpha = np.zeros(self.m)
self.b = 0.0
def predict(self, X):
# 预测类别
pred = np.sum(self.alpha * self.y * self.kernel(X, self.X), axis=1) + self.b
return np.sign(pred)
def examine_example(self, i2):
# 实现检验例子的逻辑
pass
def fit(self):
# 实现SMO算法的训练过程
pass
# 示例用法
# 你需要提供数据集X, y,惩罚参数C,容忍度tol,最大迭代次数max_iter和核函数kernel
# svm = SVM(X, y, C=1.0, tol=0.001, max_iter=100, kernel=polynomial_kernel)
# svm.fit()
# predictions = svm.predict(new_data)上述代码是一个简化的骨架,需要你完成 examine_example 和 fit 方法的具体实现。examine_example 方法负责选择第二个拉格朗日乘子,而 fit 方法则是SMO算法的主要迭代逻辑。
核函数
在机器学习中,核函数是一种用于支持向量机(Support Vector Machine,SVM)等算法的技术,它可以将输入数据映射到高维空间,从而使得在原始空间中线性不可分的问题变得线性可分。以下是一个简单的 Python 示例,演示如何实现多项式核函数和高斯核函数:
import numpy as np
def polynomial_kernel(x, y, degree=2):
"""
多项式核函数
:param x: 第一个向量
:param y: 第二个向量
:param degree: 多项式的次数
:return: 核函数的计算结果
"""
return (np.dot(x, y) + 1) ** degree
def gaussian_kernel(x, y, sigma=1.0):
"""
高斯核函数
:param x: 第一个向量
:param y: 第二个向量
:param sigma: 高斯核函数的标准差
:return: 核函数的计算结果
"""
return np.exp(-np.linalg.norm(x - y) ** 2 / (2 * (sigma ** 2)))
# 示例用法
x1 = np.array([1, 2, 3])
x2 = np.array([4, 5, 6])
# 多项式核函数
result_poly = polynomial_kernel(x1, x2, degree=2)
print(f"Polynomial Kernel Result: {result_poly}")
# 高斯核函数
result_gaussian = gaussian_kernel(x1, x2, sigma=1.0)
print(f"Gaussian Kernel Result: {result_gaussian}")
# 打印结果
# Polynomial Kernel Result: 1089
# Gaussian Kernel Result: 1.3709590863840845e-06支持向量机的应用
支持向量机在各个领域都有广泛的应用,包括:
文本分类
在社交媒体、评论和产品评价等场景中,SVM可以用于情感分析,判断文本中的情感极性(如积极、消极、中性)。
在大规模文本数据集中,SVM可以用于将文档按照不同的类别进行分类,如将文章归类到不同的主题或领域。
图像分类
在计算机视觉领域,SVM经常与图像特征提取方法结合使用,例如在HOG(Histogram of Oriented Gradients)或SIFT(Scale-Invariant Feature Transform)特征上应用SVM,以识别图像中的物体。
在人脸识别中,SVM可以通过学习正例(人脸图像)和负例(非人脸图像)之间的差异,实现对新图像的分类。
在图像检索中,SVM可以用于为图像分配标签,从而支持图像检索系统根据用户的查询找到相关的图像。
结论
支持向量机是一种强大的监督学习算法,它可以用于分类和回归问题。通过学习支持向量机,您将能够理解支持向量机的基本概念和原理,并能够实现支持向量机模型。
支持向量机的优缺点
优点
-
具有良好的泛化能力。
-
可以处理非线性问题。
缺点
-
计算复杂度高。
-
对参数的选择敏感。
支持向量机的优化
为了提高支持向量机的性能,可以采用以下方法:
-
使用 C 参数来控制超平面的复杂度。
-
使用核函数来扩充特征空间。
-
使用集成学习来提高模型的泛化能力。
第9天:随机森林
随机森林的基本概念
随机森林(Random Forest,RF)是一种集成学习算法,它由多个决策树组成。随机森林通过集成多个决策树来降低模型的过拟合风险。
随机森林的实现方法
随机森林的实现方法如下:
-
从原始数据集随机抽取样本,构建一个决策树。
-
重复步骤 1 多次,构建多个决策树。
-
对未知数据进行预测时,采用投票或平均的方式,将多个决策树的预测结果合并。
下面是一个简单的 Python 示例,演示如何使用 scikit-learn 库来实现随机森林:我们首先生成一些示例数据,然后将数据集划分为训练集和测试集。接下来,我们创建了一个包含100个决策树的随机森林模型,并使用训练数据进行训练。最后,我们使用测试数据进行预测,并计算模型的准确率。
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
import numpy as np
# 生成一些示例数据
np.random.seed(42)
X = np.random.rand(100, 2)
y = (X[:, 0] + X[:, 1] > 1).astype(int) # 简单的决策边界
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建随机森林模型
rf_model = RandomForestClassifier(n_estimators=100, random_state=42)
# 训练模型
rf_model.fit(X_train, y_train)
# 进行预测
y_pred = rf_model.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")结论
随机森林是一种强大的集成学习算法,它具有良好的泛化能力和鲁棒性。通过学习随机森林,您将能够理解随机森林的基本概念和原理,并能够实现随机森林模型。
随机森林的优缺点
优点
-
具有良好的泛化能力。
-
具有鲁棒性。
-
可以处理多分类问题。
-
可以处理连续型和离散型数据。
缺点
-
计算复杂度高。
-
对参数的选择敏感。
随机森林的优化
为了提高随机森林的性能,可以采用以下方法:
-
使用更大的决策树数量。
-
使用更少的随机特征选择。
-
使用更高的投票门限。
第10天:机器学习项目
以下是一个简单但有效的垃圾邮件过滤程序,如果想了解更多关于机器学习的实战项目,欢迎阅读Python机器学习实战:用Python构建10个有趣的应用
步骤 1: 收集数据
首先,我们需要一个包含垃圾邮件和非垃圾邮件的数据集。您可以使用已有的数据集,例如SpamAssassin Public Corpus。下载并解压缩数据集,确保您有两个文件夹,一个包含垃圾邮件,一个包含非垃圾邮件。
# 下载SpamAssassin数据集
wget https://spamassassin.apache.org/old/publiccorpus/20030228_spam_2.tar.bz2
wget https://spamassassin.apache.org/old/publiccorpus/20030228_easy_ham_2.tar.bz2
# 解压数据集
tar -xvf 20030228_spam_2.tar.bz2
tar -xvf 20030228_easy_ham_2.tar.bz2步骤 2: 数据预处理
读取数据,清理并准备进行训练。使用Python的nltk库进行文本处理:
import os
import nltk
from nltk.corpus import stopwords
from nltk.tokenize import word_tokenize
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.model_selection import train_test_split
nltk.download('stopwords')
nltk.download('punkt')
def preprocess_text(text):
stop_words = set(stopwords.words('english'))
tokens = word_tokenize(text)
tokens = [word.lower() for word in tokens if word.isalpha() and word.lower() not in stop_words]
return ' '.join(tokens)
def load_data(folder):
data = []
for filename in os.listdir(folder):
with open(os.path.join(folder, filename), 'r', encoding='latin-1') as file:
text = file.read()
preprocessed_text = preprocess_text(text)
data.append(preprocessed_text)
return data
# 加载数据
spam_data = load_data('20030228_spam_2')
ham_data = load_data('20030228_easy_ham_2')
# 创建标签
spam_labels = [1] * len(spam_data)
ham_labels = [0] * len(ham_data)
# 合并数据和标签
data = spam_data + ham_data
labels = spam_labels + ham_labels
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(data, labels, test_size=0.2, random_state=42)步骤 3: 特征提取
使用词袋模型提取文本特征:
vectorizer = CountVectorizer()
X_train_vectorized = vectorizer.fit_transform(X_train)
X_test_vectorized = vectorizer.transform(X_test)步骤 4: 训练模型
选择一个分类器,这里我们使用朴素贝叶斯:
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import accuracy_score, classification_report
# 创建并训练模型
model = MultinomialNB()
model.fit(X_train_vectorized, y_train)
# 在测试集上评估模型
predictions = model.predict(X_test_vectorized)
accuracy = accuracy_score(y_test, predictions)
print(f'Accuracy: {accuracy}')
print(classification_report(y_test, predictions))步骤 5: 部署和使用
最后,您可以将模型部署到生产环境,并使用它来过滤垃圾邮件:
def filter_spam(email_text):
preprocessed_text = preprocess_text(email_text)
vectorized_text = vectorizer.transform([preprocessed_text])
prediction = model.predict(vectorized_text)
return prediction[0] == 1
# 使用过滤器
email_text = "Congratulations! You've won a million dollars!"
if filter_spam(email_text):
print("This is a spam email.")
else:
print("This is not a spam email.")
演示结果:
请注意,这只是一个简单的垃圾邮件过滤器示例。在实际情况中,您可能需要更复杂的模型,处理更多的特征,并进行更详细的调优。此外,垃圾邮件过滤是一个不断演化的领域,可能需要定期更新模型以适应新的垃圾邮件技巧。