【C语言】链表入门（配图）

链表（LinkList）概念

链表是一种数据结构，它由一系列节点组成，每个节点包含两个部分：数据和指向下一个节点的指针。链表中的节点可以在运行时动态添加或删除，因此它具有很好的灵活性。与数组不同，链表中的节点不必在内存中连续存储，因此它可以更有效地利用内存。链表可以用于实现队列、栈、哈希表等数据结构。

链表的分类

链表可以分为单向链表、双向链表和循环链表。

单向链表中每个节点只有一个指针，指向下一个节点；

双向链表中每个节点有两个指针，分别指向前一个节点和后一个节点；

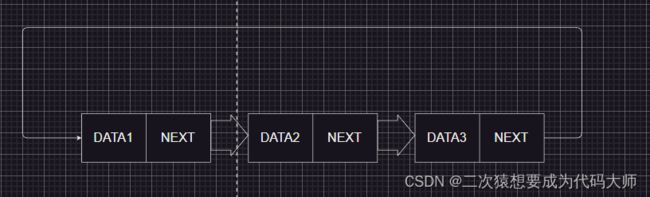
循环链表是一种特殊的链表，它的最后一个节点指向第一个节点，形成一个环。

---

单向链表

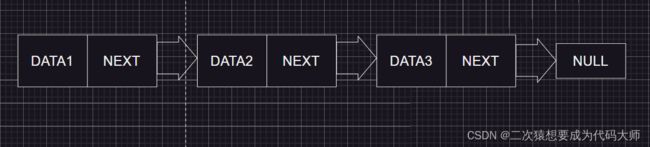
单向链表是一种链表，每个节点只有一个指针，指向下一个节点。它的优点是插入和删除节点的时间复杂度为O(1)，但查找节点的时间复杂度为O(n)。单向链表的头节点指向第一个节点，尾节点指向最后一个节点的下一个节点，即NULL。

什么是结点？

结点是链表中的基本单元，它包含一个数据元素和一个指向下一个结点的指针。

                                    

                                                          这是一个单向链表结点

                                                            这是一个单向链表

直接上代码

这是结点的创建方法

typedef struct Node{
    int date;         //数据域
    struct Node *next //指针域（存放下一个结点的位置）
}Node;

结点也可以分为三种：单向链表结点、双向链表结点、循环链表结点，分别出现在三种链表当中。

>关于头结点和首元节点的区别：

头结点 是在链表头部添加的一个不存储数据的节点，它的作用是方便对链表的操作，如插入、删除等。

首元节点 是链表中第一个存储数据的节点，它是链表的第一个有效节点，也是链表的起点。

有头结点：方便使用头插法插入元素

此为链表的初始化（只生成头结点）

typedef struct Node{
    int data;          //数据域
    struct Node *next; //指针域
}Node,*LinkList;
//Node struct Node 的别名 LinkList struct Node *
//int   int*
LinkList create(){
    //动态申请空间（head指针指向这个空间）
    LinkList head=(Node *)malloc(sizeof(Node));
    
    //判断空间是否开辟成功
    if(head==NULL){
        printf("空间开辟失败！\n");
        return NULL;
    }
    //头结点，指针域赋值为NULL
    head->next=NULL;
    
    //返回头结点指针
    return head;
}

学习单向链表需要注意指针的使用，因为链表的节点是通过指针连接的。在插入或删除节点时，需要注意指针的指向，否则可能会导致链表断裂或内存泄漏。此外，需要注意链表的头节点和尾节点的处理，以及链表为空的情况。 

这是单向链表的创建插入并删除

//定义单向链表结点
typedef struct Node{
    int data;         //数据域
    struct Node *next; //指针域（存放下一个结点的位置）
}Node;

//创建链表
Node* createList(int n){
    Node *head, *p, *q;
    head = (Node*)malloc(sizeof(Node)); //创建头结点
    head->next = NULL; //头结点指针域为空
    q = head; //q指向头结点
    for(int i=0; idata); //输入新结点数据
        p->next = NULL; //新结点指针域为空
        q->next = p; //将新结点插入到链表尾部
        q = p; //q指向新结点
    }
    return head; //返回头结点
}

//插入结点
Node* insertNode(Node *head, int pos, int data){
    Node *p, *q;
    p = (Node*)malloc(sizeof(Node)); //创建新结点
    p->data = data; //新结点数据域为data
    p->next = NULL; //新结点指针域为空
    q = head; //q指向头结点
    for(int i=0; inext; //q指向插入位置的前一个结点
    }
    p->next = q->next; //将新结点插入到链表中
    q->next = p;
    return head; //返回头结点
}

//删除结点
Node* deleteNode(Node *head, int pos){
    Node *p, *q;
    q = head; //q指向头结点
    for(int i=0; inext; //q指向删除位置的前一个结点
    }
    p = q->next; //p指向要删除的结点
    q->next = p->next; //

双向链表

双向链表是一种链表结构，每个节点有两个指针域，分别指向前驱节点和后继节点。相比于单向链表，双向链表可以双向遍历，查找节点的时间复杂度为O(n/2)，插入和删除节点的时间复杂度为O(1)。但是，双向链表的每个节点需要额外的一个指针域，占用更多的内存空间。

                          

                                                      这是一个双向链表结点

                                                          这是一个双向链表

创建代码如下

Node* insertNode(Node* head, int data, int position) {
    Node* newNode = createNode(data); // 创建新结点
    if (position == 0) { // 如果要插入的位置是头结点
        newNode->next = head; // 新结点的后继指向头结点
        head->prev = newNode; // 头结点的前驱指向新结点
        return newNode; // 返回新的头结点
    }
    Node* curr = head;
    for (int i = 0; i < position - 1; i++) { // 找到要插入位置的前一个结点
        curr = curr->next;
    }
    newNode->next = curr->next; // 新结点的后继指向要插入位置的结点
    newNode->prev = curr; // 新结点的前驱指向要插入位置的前一个结点
    if (curr->next != NULL) { // 如果要插入位置的结点不为空
        curr->next->prev = newNode; // 要插入位置的结点的前驱指向新结点
    }
    curr->next = newNode; // 要插入位置的前一个结点的后继指向新结点
    return head; // 返回头结点
}

int main() {
    int arr[] = {1, 2, 3, 4, 5};
    int size = sizeof(arr) / sizeof(arr[0]);
    Node* head = createLinkedList(arr, size);
    Node* curr = head;
    while (curr != NULL) {
        printf("%d ", curr->data);
        curr = curr->next;
    }
    return 0;
}

那么双向链表是怎么插入的呢  

                                                                        如图所示

双向链表插入代码如下

Node* insertNode(Node* head, int data, int position) {
    Node* newNode = createNode(data);
    if (position == 0) {
        newNode->next = head;
        head->prev = newNode;
        return newNode;
    }
    Node* curr = head;
    for (int i = 0; i < position - 1; i++) {
        curr = curr->next;
    }
    newNode->next = curr->next;
    newNode->prev = curr;
    if (curr->next != NULL) {
        curr->next->prev = newNode;
    }
    curr->next = newNode;
    return head;
}

那么双向链表是怎么删除的呢  

                                                                      如图

双向链表删除代码如下

Node* deleteNode(Node* head, int position) {
    if (head == NULL) { // 如果链表为空，直接返回
        return NULL;
    }
    Node* curr = head;
    if (position == 0) { // 如果要删除的是头结点
        head = head->next; // 头结点指向下一个结点
        if (head != NULL) { // 如果下一个结点不为空
            head->prev = NULL; // 下一个结点的前驱指向空
        }
        free(curr); // 释放当前结点
        return head; // 返回新的头结点
    }
    for (int i = 0; i < position; i++) { // 找到要删除的结点
        curr = curr->next;
        if (curr == NULL) { // 如果找不到，直接返回
            return head;
        }
    }
    curr->prev->next = curr->next; // 要删除结点的前驱指向要删除结点的后继
    if (curr->next != NULL) { // 如果要删除结点的后继不为空
        curr->next->prev = curr->prev; // 要删除结点的后继的前驱指向要删除结点的前驱
    }
    free(curr); // 释放当前结点
    return head; // 返回头结点
}

两种链表的查找都一样，如下

void search(LinkList head){
	if(!head){
		return;
	}
	int num;
	printf("输入要查找的数据：");
	scanf("%d",&num);
	Node *p=head->next;
	while(p){
		if(num==p->data){
			printf("链表存在数据");
			return;
		}
		p=p->next;
	} 
	printf("不存在此数据");
}

双向链表与单向链表的区别

双向链表与单向链表的区别在于，每个结点不仅有一个指向后继结点的指针，还有一个指向前驱结点的指针。这样，我们就可以在双向链表中方便地进行双向遍历、插入和删除操作。在插入和删除操作中，我们需要注意更新前驱和后继结点的指针，以保证链表的正确性。在双向链表中，头结点的前驱指向空，尾结点的后继指向空。

循环链表

循环链表是一种特殊的链表，它的最后一个结点的后继指向第一个结点，形成一个环。循环链表可以是单向的，也可以是双向的。在循环链表中，我们可以从任意一个结点开始遍历整个链表，直到回到起点。循环链表的插入和删除操作与普通链表类似，但需要注意处理头尾结点的指针。在循环链表中，头结点的前驱指向尾结点，尾结点的后继指向头结点。

                                                             这是一个循环链表

循环链表的创建

Node* createLinkedList(int arr[], int size) {
    Node* head = createNode(arr[0]); // 创建头结点
    Node* tail = head; // 将尾结点指向头结点
    for (int i = 1; i < size; i++) {
        Node* newNode = createNode(arr[i]); // 创建新结点
        tail->next = newNode; // 将尾结点的后继指向新结点
        newNode->prev = tail; // 将新结点的前驱指向尾结点
        tail = newNode; // 将尾结点指向新结点
    }
    tail->next = head; // 将尾结点的后继指向头结点，形成循环链表
    head->prev = tail; // 将头结点的前驱指向尾结点，形成循环链表
    return head; // 返回头结点
}

int main() {
    int arr[] = {1, 2, 3, 4, 5};
    int size = sizeof(arr) / sizeof(arr[0]);
    Node* head = createLinkedList(arr, size);
    Node* curr = head;
    do { // 使用 do-while 循环遍历循环链表
        printf("%d ", curr->data);
        curr = curr->next;
    } while (curr != head); // 当遍历到头结点时结束循环
    return 0;
}

 循环链表的中间插入和中间删除与单链表一致

Node* insertNode(Node* head, int data, int position) {
    Node* newNode = createNode(data); // 创建新结点
    if (position == 0) { // 如果要插入的位置是头结点
        newNode->next = head; // 新结点的后继指向头结点
        head->prev->next = newNode; // 将尾结点的后继指向新结点
        newNode->prev = head->prev; // 将新结点的前驱指向尾结点
        head->prev = newNode; // 将头结点的前驱指向新结点
        return newNode; // 返回新的头结点
    }
    Node* curr = head;
    for (int i = 0; i < position - 1; i++) { // 找到要插入位置的前一个结点
        curr = curr->next;
    }
    newNode->next = curr->next; // 新结点的后继指向要插入位置的结点
    newNode->prev = curr; // 新结点的前驱指向要插入位置的前一个结点
    if (curr->next != head) { // 如果要插入位置的结点不是头结点
        curr->next->prev = newNode; // 要插入位置的结点的前驱指向新结点
    } else { // 如果要插入位置的结点是头结点
        head->prev = newNode; // 将头结点的前驱指向新结点
    }
    curr->next = newNode; // 要插入位置的前一个结点的后继指向新结点
    return head; // 返回头结点
}


Node* deleteNode(Node* head, int position) {
    if (head == NULL) { // 如果链表为空，直接返回
        return NULL;
    }
    Node* curr = head;
    if (position == 0) { // 如果要删除的是头结点
        head = head->next; // 头结点指向下一个结点
        if (head != NULL) { // 如果下一个结点不为空
            head->prev = NULL; // 下一个结点的前驱指向空
        }
        free(curr); // 释放当前结点
        return head; // 返回新的头结点
    }
    for (int i = 0; i < position; i++) { // 找到要删除的结点
        curr = curr->next;
        if (curr == head) { // 如果找到头结点，直接返回
            return head;
        }
    }
    curr->prev->next = curr->next; // 要删除结点的前驱指向要删除结点的后继
    curr->next->prev = curr->prev; // 要删除结点的后继指向要删除结点的前驱
    free(curr); // 释放当前结点
    return head; // 返回头结点
}

 学习循环链表需要注意

循环链表的删除操作与普通链表类似，但需要注意处理头尾结点的指针。
在循环链表中，头结点的前驱指向尾结点，尾结点的后继指向头结点。
在删除操作中，如果要删除的结点是头结点，需要将头结点指向下一个结点，并将下一个结点的前驱指向空。
如果要删除的结点是尾结点，需要将尾结点指向前一个结点，并将前一个结点的后继指向头结点。
如果要删除的结点是中间结点，需要将要删除结点的前驱指向要删除结点的后继，将要删除结点的后继指向要删除结点的前驱。

链表为什么查询慢增删快

链表为什么查询慢增删快的原因是，链表中的每个结点都需要通过指针来访问其它结点，而指针的访问速度比数组的访问速度慢。在查询操作中，需要遍历整个链表才能找到目标结点，时间复杂度为 O(n)。而在插入和删除操作中，只需要修改相邻结点的指针，时间复杂度为 O(1)。因此，链表适合频繁进行插入和删除操作，但不适合频繁进行查询操作。

                                ​​​​​​​        

在数组中我们讲了为什么数组查询快，增删慢，

ArrayList和LinkedList都是线性表的实现方式，但它们的内部实现方式不同。ArrayList是基于数组实现的，可以随机访问元素，但插入和删除操作需要移动元素，时间复杂度为 O(n)。LinkedList是基于链表实现的，插入和删除操作只需要修改相邻结点的指针，时间复杂度为 O(1)，但查询操作需要遍历整个链表，时间复杂度为 O(n)。因此，ArrayList适合频繁进行查询操作，而LinkedList适合频繁进行插入和删除操作。

后续我应该会更加详细的讲述这两个的区别，敬请期待。