贪心算法例题

贪心算法经典例题解析

贪心法：遵循某种规律，不断贪心的选取当前最优策略的算法设计方法。

例一：分糖果

已知一些孩子和一些糖果，每个孩子有需求因子g，每个糖果有大小s，当某个糖果的大小s >= 某个孩子的需求因子g时，代表该糖果可以满足该孩子；求使用这些糖果，最多能满足多少孩子？(注意，某个孩子最多只能用1个糖果满足)例如，需求因子数组g = [5, 10, 2, 9, 15, 9]；糖果大小数组s = [6, 1, 20, 3, 8]；最多可以满足3个孩子
思考：　　
1、当某个孩子可以被多个糖果满足时，是否需要优先用某个糖果满足这个孩子？
　　优先用最小的糖果满足孩子
2、当某个糖果可以满足多个孩子时，是否需要优先满足某个孩子？
　　优先满足需求大的孩子
贪心策略：
1、某个糖果不能满足某个孩子时，则该糖果也一定不能满足需求因子更大的孩子。
2、某个孩子可以用更小的糖果满足，则没必要用更大糖果满足，因为可以保留更大的糖果满足需求因子更大的孩子。（贪心）
3、孩子的需求因子更小则更容易被满足，故优先从需求因子小的孩子尝试，可以得到正确的结果。

算法思路：
　　1、对需求因子数组g与糖果大小数组s进行从小到大的排序。
　　2、按照从小到大的顺序使用糖果尝试是否可以满足某个孩子，每个糖果只尝试一次；若尝试成功，则换下一个孩子尝试，直到没有发现没有更多的孩子或者没有更多的糖果，循环结束。

class Solution {
public:
int findContentChildren(vector& g, vector& s) {
// 对g和s进行排序
    sort(g.begin(),g.end());
    sort(s.begin(),s.end());
    int child = 0;
    int cookie = 0;
    while(child < g.size() && cookie < s.size()){
	    if(s[cookie] >= g[child]){
	    	child++;
		}
		cookie++;
	}
		return child;
	}
};

状态机的概念

图中每个圆代表一个状态，每个箭头表示一个if-else关系

例二：摇摆数组(376)

题目： 一个整数序列，如果两个相邻元素的差恰好正负(负正)交替出现，则该序列被称为摇摆序列。一个小于2个元素的序列直接为摇摆序列。
例如:
　　序列[1, 7, 4, 9, 2, 5]，相邻元素的差(6, -3, 5, -7, 3)，该序列为摇摆序列。
　　序列[1,4,7,2,5] (3, 3, -5, 3)、[1,7,4,5,5] (6, -3, 1, 0)不是摇摆序列。
　　给一个随机序列，求这个序列满足摇摆序列定义的最长子序列的长度。
例如:
　　输入[1,7,4,9,2,5]，结果为6；输入[1,17,5,10,13,15,10,5,16,8]，结果为7([1,17,10,13,10,16,8])；输入[1,2,3,4,5,6,7,8,9]，结果为2。
解题思路(贪心思想)：
　　当序列有一段连续的递增(或递减)时，为形成摇摆子序列，我们只需要保留这段连续的递增(或递减)的首尾元素（最大或最小），这样更可能使得尾部的后一个元素成为摇摆子序列的下一个元素。

										 [1,17,5,10,13,15,10,5,16,8]    

class Solution {
public:
    int wiggleMaxLength(vector& nums) {
        if(nums.size() < 2)
            return nums.size();
        static const int BEGIN = 0;
        static const int UP = 1;
        static const int DOWN = 2;
        int STATE = BEGIN;
        int max_length = 1; // 摇摆序列最大长度最少为1
        // 循环处理nums中的数据
        for(int i = 1;i < nums.size(); i++)
        {
            switch(STATE){
            case BEGIN:
                if(nums[i] > nums[i-1]){
                    STATE = UP;
                    max_length++;
                }
                else if(nums[i] < nums[i-1]){
                    STATE = DOWN;
                    max_length++;
                }
                break;
            case UP:
                if(nums[i] < nums[i-1]){
                    max_length++;
                    STATE = DOWN;
                }
                break;
            case DOWN:
                if(nums[i] > nums[i-1]){
                    max_length++;
                    STATE = UP;
                }
                break;
            }
        }
        return max_length;
    }
};   

例三：移除K个数字(402)

已知一个使用字符串表示的非负整数num，将num中的k个数字移除，求移除k个数字后，可以获得的最小的可能的新数字。（num不会以0开头，num长度小于10002）
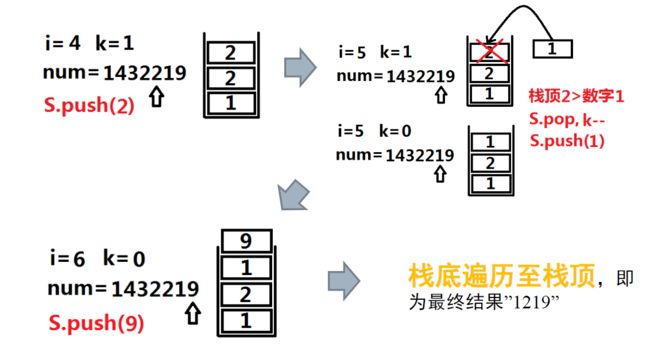
例如：输入：num=“1432219”，k=3
　　在去掉3个数字后得到的很多种可能中，如1432、4322、2219、1219、1229…；去掉数字4、3、2得到的1219最小！
贪心解题思路：
　　从高位向低位遍历，如果对应的数字大于下一位数字，则把该数字去掉，得到的数字最小。
暴力解法：
　　去掉k个数字，即从最高位遍历k次。
用栈进行优化：

1.当所有数字都扫描完成后，k仍然>0，应该做怎样的处理？例如: num = 12345，k = 3 时。
　　**答：**如果扫描完成后k依然大于0，则从字符串最后删除元素
2.当数字中有0出现时，应该有怎样的特殊处理？例如: num = 100200, k = 1 时。
　　**答：**如果为0但是栈不为空则入栈，否则不入栈
3.如何将最后结果存储为字符串并返回?
　　**答：**可以用vector代替栈，因为队列可以进行尾部插入（back_push）和尾部删除(back_pop),删除完成后对队列进行头部出队（front_pop）并赋值给字符串

class Solution {
public:
    string removeKdigits(string num, int k) {
        // 定义一个vector，充当栈
        vector S;
        string result="";
        // 循环遍历字符串
        for(int i = 0 ;i < num.length();i++){
            int number = num[i] - '0';
            while(S.size() != 0 && S.back() > number && k>0){
                S.pop_back();
                k--;
            }
            if(number != 0 || S.size() != 0)  // 不为0或者不为空都入栈
            {
                S.push_back(number);
            }
        }
        while(k>0 && S.size() != 0)
        {
            S.pop_back();
            k--;
        }

        for(int i= 0;i