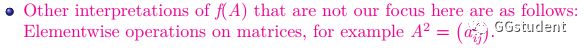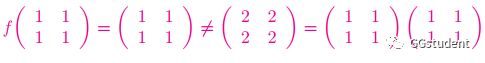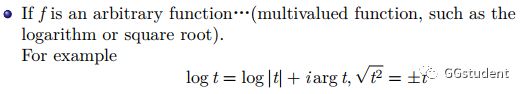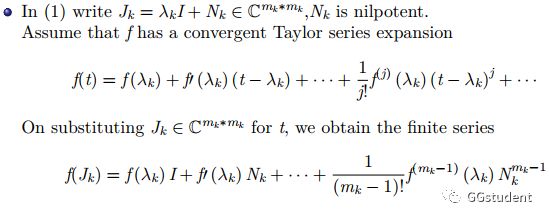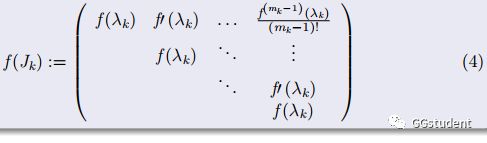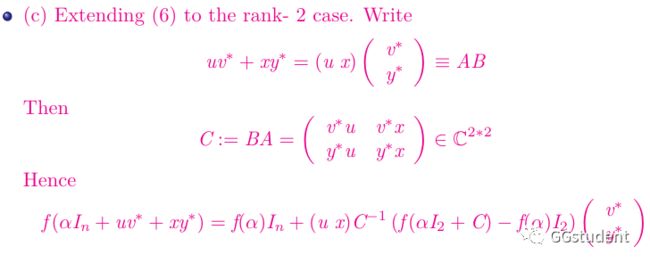矩阵用jordan解决initial-value问题_矩阵函数第一章

1.简介

    首先我们要明确我们的研究对象

    矩阵函数就是以矩阵为自变量的函数.

    我们很早就已经学过以矩阵为自变量的函数,比如说trace(迹,就是矩阵对角元的总和),det(矩阵的行列式),以及矩阵转置.它们它们分别是from n级复矩阵 to 复数,以及from n级复矩阵 to n级复矩阵的映射.

    而我们的研究矩阵函数,是from n级复矩阵 to n级复矩阵的映射.

    f是一个标量函数,而A是一个n级复矩阵,那我们应该怎样定义一个n级复矩阵f(A)呢?

    一种简单的方法是,既然f是一个标量函数,那我就考虑f直接作用到矩阵的每个元素上.比如函数f:x->x^2.

    

    但我们知道矩阵自己有它自己乘法定义,如果采用上述定义得到的f(A)=A^2,得到的A^2与矩阵乘法不相容,即.

    所以说,这种f直接作用到矩阵的每个元素上的定义手法,没有很好的代数性质,所以不予考虑.

    那应该采取怎样的定义,才能克服这个缺点呢?

   当f(t)是多项式的时候,一种自然地定义矩阵函数的方法,就是把多项式中的不定元t用矩阵A代入(一元多项式环的通用性质).这将会是我们后面所有定义的出发点,也就是我们后面要给定的矩阵函数f(A),当f是一个多项式的时候,f(A)的结果就应该是f(t)中的不定元t用A代入的结果.

    而上图中,f(t)是一个有理函数,也可以考虑t用矩阵A代入,而由于涉及到矩阵求逆的问题,所以还要求1不是矩阵A的特征值.

    更一般地考虑,如果f有一个收敛的幂级数表示,如果上图所示,ln(1+t)可以写成一个幂级数表示,而幂级数的矩阵函数是前面已经有定义了,就是把不定元t用矩阵A代入,所以自然地给出矩阵函数ln(I+A)的定义.但因为幂级数表示要收敛,所以要求t的绝对值要小于1,而在矩阵函数中则是要求A的谱半径,也就是A的特征值的最大值要小于1.

    更一般的如果,t是任意的函数,比如说是多值函数应该怎么定义他的矩阵函数呢?

2.定义

    我们将会介绍三种定义手法.第一种定义手法是通过Jordan标准型来定义的;第二种定义手法是通过Hermite插值来定义的;第三种定义手法是通过复变函数里的Cauchy积分定义的.

    **先看第一种定义手法**

   

    我们知道一个n级复矩阵一定有Jordan标准型(存在性证明可以看丘维声编的《高等代数(下册)——大学高等代数课程创新教材. 》)

    (1)式中,J表示矩阵A的Jordan标准型,

    J_1,...,J_p表示对应的Jordan块;

    值得注意的是矩阵Z也是不唯一,Jordan块可以调换排列顺序,所以J也并不唯一.

    λ_1,...,λ_s表示矩阵A的s个互异的特征值;

    我们把出现了λ_i的特征值的各个Jordan块的阶数的最大值,称为λ_i的指数n_i(index).

    注意特征值的指数不同于代数重数,几何重数,比如说这面这个矩阵的,特征值0的指数是2,代数重数是4,几何重数是3.

 

    接着要给出函数f在矩阵A的谱上的定义.

    然后就可以给出矩阵函数的定义如(3)所示.f(A)的定义,就看f(J)是如何定义,而J是分块对角矩阵,就看f是如何作用在每个分块上,即关键在于怎么定义f(J_k),我觉得直接给出f(J_k)的定义不太自然,所以我们先看下面这个事实.

    第一个事实,Jordan块J_k可以表示成一个数量矩阵λ_k*I和一个幂零矩阵N_k的和.也就是J_k=λ_k*I+N_k,就是J_k-λ_k*I=N_k是一个幂零矩阵.

    第二个事实,考虑f(t)在t=λ_k处的Taylor展式,注意到Taylor展式是一个幂级数求和,他涉及到一个级数是否收敛的问题.但是对于Taylor展式而言,也就是对这个多项式而言,我们刚才已经说了,可以考虑不定元t用矩阵J_k代入,然后注意到N_k是一个幂零矩阵,所以f(J_k)只是有限个矩阵求和的结果,从而避免了收敛的问题.

    所以,我们得到了f(J_k)的矩阵函数如下

    但是有以下几个问题需要注意

    首先我们在定义f(A)的时候,需要先对A做Jordan分解,而我们已经说过Jordan分解的结果是不唯一的,所以我们不禁要问,不同的Jordan分解是否会得到不同的f(A)呢?我们的回答:不同的Jordan分解是否会得到的f(A)是一样的.理由如下:

    第二个问题,由A得到的矩阵函数f(A)要想能表示成关于A的多项式,而当f是一个多值函数的时候,我们要先f的取值做一个限制,将其限制在一个分支上.否则将会出现以下问题.

    比如f是一个开平方函数,那f(1)既可以是1也可以是-1.现考虑将其作用到2级单位矩阵I上,如果一开始限制f(1)结果只能是1,那么得到的矩阵函数就是I,如果一开始限制f(1)结果只能是-1,那么得到的矩阵函数就是-I.如果不加限制,比如第一个Jordan块取f(1)=1,第二个Jordan块取f(1)=-1,那么得到的矩阵函数就是diag(1,-1),显然找不到一个多项式p,使得diag(1,-1)=p(I).

    **第二种定义手法**

    给出定义之前,我们先思考,矩阵函数f(A)是由什么决定,自然会回答,那就是由矩阵A和函数f决定啊.那我们可以看下面这一个例子.

    这个例子说明,相同的函数,作用在不同的矩阵上,可以有相同的结果;相同的矩阵,被不同的函数作用,也可以有相同的结果;不同的函数作用到不同的矩阵上,也可以有相同的结果.

    所以我们思考:决定矩阵更关键的因素是什么?

    首先多项式的矩阵函数都是已经定义好的,所以我们从多项式出发,看以下的Thm 1.3.

    Thm 1.3说明,对于两个多项式p,q而言,只要p,q在矩阵A的谱上的取值是相同的,那么得到的矩阵函数p(A),q(A)是相同的.(所谓"在矩阵A的谱上的取值"可以看前面的(2)式)

    也就是说,对于多项式而言,矩阵函数由多项式在矩阵的谱上的取值所决定.也就是只要多项式在矩阵的谱上的取值给定了,那么这个矩阵函数也就确定了.

    所以,对于任意函数f而言,只要f在矩阵A的谱上的取值给定了,那么我们要定义的矩阵函数应该也是确定的,也就是我们定义的矩阵函数他的结果应该是唯一的.

    定义1.4,是出于这样的想法,首先,对于多项式p而言,矩阵函数p(A)是有定义的,所以我们可以借助p(A)来定义f(A)=p(A),但是这个多项式p应该找呢?或者说怎样的p应该满足什么性质?那就是p和f在矩阵A的谱上的取值是一样的,也就是上图的(5)式.根据Hetmite插值多项式的性质,我们知道,次数小于矩阵A最小多项式次数的多项式p是存在且唯一的.

    既然p是唯一的,那么p(A)就是唯一的,那么f(A)=p(A)就是一个确定的结果,仅此足以.

    下图给出了p的显式表达,仅供参考.

    备注1.5说的是,设q是一个多项式,而p是定义1.4找到的Hermite插值多项式,这是两个多项式,它们的次数可以不同,但是只要p,q在矩阵A的谱上的值是相同的,那么得到的矩阵函数p(A),q(A)就是相同的;同时,当f=q是多项式时,f(A)就是不定元用矩阵A代入.

    目前为止,我们已经提出了两种矩阵函数的定义方法,我们不禁要问,这两种定义手法对于同一的函数,以及同一个矩阵而言,得到的矩阵函数是否是一样的?

    备注1.10告诉我们对于Jordan块J_k而言,由定义1.4找到的Hermite插值多项式,就是f在t=λ_k处的一个Taylor展式.由此可见,定义1.4和定义1.2对Jordan块J_k而言,得到的矩阵函数f(J_k)是相同.

    我们是否能把结论推广到对于一般的矩阵呢?我们的答案:可以.

    **第三种定义手法**

    第三种定义手法是通过复变函数里的Cauchy积分定理来定义的.

    还涉及到了矩阵求逆,所以要求A的特征值不能落在闭合曲线Γ上.

    由于等号右边的逆矩阵的每个元素都是关于t的函数,而对这个逆矩阵求"定积分",就是对这个每个逆矩阵的每个元素求定积分.

    同时由于我们引入了新的定义手法,我们还要证明,第三种定义方法和前面两种定义手法的等价性.

3.性质

    简单说一句,证明上述性质时,在不同的场景采用不同的定义方法会给证明提供方便,比如涉及矩阵特征值的时,采用Jordan分解的手法;在谈论与f作用有关的交换性时,采用Hermite插值的手法.

    定理1.14说,函数f,g如果在A的谱上的值是一样的,那么两个矩阵函数就是一样的.

    定理1.15,对于标量函数,他可以做加法,乘法.那么矩阵函数也可以做加法,乘法.并且函数先做加法(或者乘法)再作用到矩阵A上,和函数先作用在矩阵A上得到矩阵函数再对矩阵函数作加法(或者乘法),得到的结果是一样的.

    定理1.17因为我们讨论的矩阵函数h:它把n级复矩阵A映射成另一个n级复矩阵h(A),所以我们可以考虑另外一个矩阵函数g:他把n级复矩阵h(A)映射成另一个n级复矩阵g(h(A)),这个过程可以看成是一个复合函数g*h:他把n级复矩阵A映射成另一个n级复矩阵g(h(A)).当然这里的g,h都要满足一定的条件,复函矩阵函数才有定义.

    定理1.18谈论的是共轭转置和函数作用的交换性.

    要求f在复平面的一个子集Ω上是解析的,而且对于Ω的每个连通分支对于共轭运算是封闭的,即关于实轴对称.

    同时还要要求被f作用的矩阵,他的特征值都要在这个Ω上.

    f作为标量函数,自然可以讨论他的连续性.同样地,我们可以去讨论矩阵函数的连续性,考虑到第一种手法里,对f的原函数以及若干阶导数的要求,所以这里为了后顾之忧,直接假设f有n-1阶的连续的导数.

    所谓连续性就是对于矩阵A,我们考虑一个小扰动E(也就是同阶的矩阵),则f(A)与f(A+E)之间也是相差一个小扰动.(或者理解成n^2元向量值函数的连续性即可.)

    首先我们要求这里的矩阵A,他的谱要落在D上,而函数f在D上是有定义的,所以f(A)是有定义的.同时因为我们考虑的E是一个小扰动,所以A+E的谱与A的谱也是相差不大,且因为D是一个开集,既然f在A的谱上有定义,也就是D上的某些点上定义,所以在这些点周围的一个小邻域内也是有定义的.所以f(A+E)也是有定义的.

    定理1.21说的是A是一个特殊的分块上三角矩阵的时,矩阵函数f(A)的表达式.

4.非初等矩阵函数

5.矩阵平方根与矩阵对数的存在性

然后给出矩阵平方根,以及矩阵对数的表达式

    在众多的矩阵平方根(矩阵对数)的表达式,存在唯一的一个特殊的矩阵平方根,并且对于这个唯一的结果,有一个特别的记号.

5.一些计算实例

    根据前面给出的矩阵函数定义,可以看到我们计算f(A),要先去找A的谱.

    问有没有办法可以不去计算A的谱就可以直接得到f(A)呢?

    **第1个情形:单位矩阵+秩1矩阵**

    **第2个情形:幂等矩阵**

    **第3个情形:离散Fourier变换矩阵**

6.f(AB)与f(BA)

    推论1.34告诉我们,m和n不总是相等的,当m,n不等的时候,矩阵BA和矩阵AB的的维数也会一大一小,而(8)描述的就是一个大维数的矩阵函数和小维数的矩阵函数之间的转化关系.

    (b)这里的f是求逆函数即x->x^(-1)

    (c)的结论是一个特殊的n级矩阵函数,可以转化为一个2级矩阵C的求逆问题,和一个2级矩阵函数的计算问题,前者是一个简单的结果,而后者可以看后面的(d).

7.总结

主要有以下四点内容

1.矩阵函数是怎么定义的
2.以及这种定义的合理性,等价性
3.以及这样定义,会得到怎么性质,结果
4.讨论了对于特定的矩阵,有没有可以不通过Jordan分解,直接得到它的矩阵函数

8.后期工作

对于特殊的函数,或者特殊的矩阵,比如图的Laplace矩阵,有没有直接计算矩阵函数的方法.

0.致谢

谢谢吴老师参与到我的试讲环节,给我要讲解的内容框架以及编排提供了宝贵的意见.

最后也祝妈妈11月15号生日快乐.