代码随想录刷题笔记（DAY2）

今日总结：今天在学 vue 做项目，学校还有很多作业要完成，熬到现在写完了三道题，有点太晚了，最后一道题的题解明天早起补上。（补上了）

Day 2

01. 有序数组的平方（No. 977）

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

1.1 笔记

这道题我一开始是准备使用比较器根据绝对值排序来实现的，但是 Comparator 是无法作用于 int[] 的，小小踩坑

然后回想起昨天的双指针思想，这道题可以通过两个分别指向负数和正数的，因为是非递减排序的，所以负数是按照绝对值非递增排序的，也就是前一个负数的绝对值一定大于后一个负数的绝对值，平方也同理。

所以不妨设置一个新数组来存储这些元素，利用 left 指针去遍历小于零的元素，right 指针去遍历大于零的元素，当遍历结束后（如果有）剩余的元素，也就是正数和负数个数不相等的情况，就按照绝对值的顺序继续放入新数组。

1.2 代码

class Solution {
    public int[] sortedSquares(int[] nums) {
        int left = 0;
        int right = nums.length - 1;
        int[] resArr = new int[nums.length]; // 存储结果的新数组
        int index = resArr.length - 1; // 从后往前循环赋值新数组
        // 正数组直接返回结果
        if (nums[left] >= 0) {
            for (int i = 0; i < nums.length; i++) {
                nums[i] = nums[i] * nums[i];
            }
            return nums;
        }
        // left 索引负数部分，right 索引整数部分
        while (nums[left] < 0 && nums[right] >= 0) {
            if (Math.abs(nums[left]) > nums[right]) {
                resArr[index] = nums[left] * nums[left];
                index--;
                left++;
            } else if (Math.abs(nums[left]) < nums[right]) {
                resArr[index] = nums[right] * nums[right];
                index--;
                right--;
            } else {
                // 相等的情况，赋值两次
                resArr[index] = nums[left] * nums[left];
                index--;
                resArr[index] = nums[left] * nums[left];
                index--;
                left++;
                right--;
            }
        }
        if (nums[left] >= 0) {
            // 负数部分已经遍历完，处理正数部分
            for (int i = index; i >= 0; i--) {
                resArr[i] = nums[right] * nums[right];
                right--;
            }
        } else if (nums[right] < 0) {
            // 说明正数部分已经遍历完了
            for (int i = index; i >= 0; i--) {
                resArr[i] = nums[left] * nums[left];
                left++;
            }
        }
        return resArr;
    }
}

02. 长度最小的子数组（No. 209）

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

2.1 笔记

这道题采用的是滚动数组的方法，所谓滚动数组就是不断的调节子序列的起始和终止的位置，从而得出我们想要的结果，首先要考虑的是我们遍历的是数组的起始位置还是终止位置，如果遍历的是起始位置的话那终止位置该如何确定？通过 for 循环继续向后遍历，来确定以每个元素为起始元素所得到的所有的子数组，这样就是暴力解法，显然时间复杂度是不符合题目要求的。

所以我们采用 for 循环遍历终止位置，那要考虑的就是，我们的起始位置该什么时候更新呢？很明显，当我们循环遍历直到这个数组的 sum 和大于等于题目中的 target 起始位置向后移动缩小范围，这样就避免了暴力解法中我们每到一个起始位置都要从头开始加和：通过起始位置的向后递增，这时候我们的 sum 应该等于原本的 sum 减去每次的 nums[i] **直到 **我们发现 sum < target 就再去更新终止位置的值，这样就实现了数组滚动前进的效果，遍历以 nums 中的每个元素作为结尾的所有子数组。

2.2 代码

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int i = 0; // 起点
        int minLen = Integer.MAX_VALUE;
        int sum = 0;
        for (int j = 0; j < nums.length; j++) {
            // 外层去循环遍历滑动窗口的终点，起点在找到符合的区间再更新
            sum += nums[j];
            // 一直使起始位置向后移动直到 sum < target 为止
            while (sum >= target) {
                // 更新最短的值
                minLen = Math.min(minLen, (j - i + 1));
                // 移动起始位置
                sum -= nums[i];
                i++;
            }
        }
        return minLen == Integer.MAX_VALUE ? 0 : minLen;
    }
}

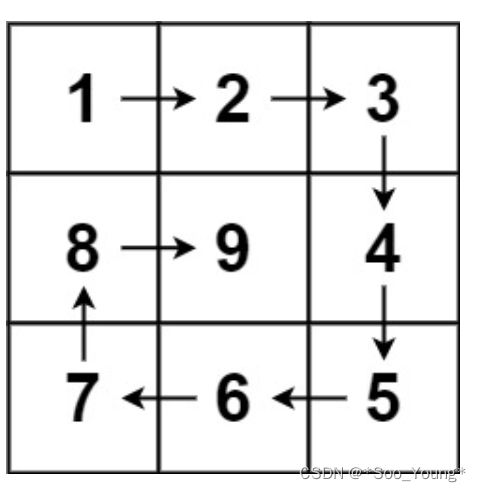
03. 螺旋矩阵 II（No. 59）

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

3.1 笔记

这道题的难点是每条边的边界处理的方法，比如最后一个节点要不要取，如果盲目的写的话很容易出现错误，下面我们来引入循环不变量的思想：

在计算机科学中，循环不变性（loop invariant，或“循环不变量”），是一组在循环体内、每次迭代均保持为真的性质，通常被用来证明程式或伪码的正确性（有时但较少情况下用以证明算法的正确性）。简单说来，“循环不变性”是指在循环开始和循环中，每一次迭代时为真的性质。这意味着，一个正确的循环体，在循环结束时“循环不变性”和“循环终止条件”必须同时成立。

由于循环和递归的相通，证明带有不变性的循环的部分正确性和证明通过归纳的递归程序的正确性极其相似。

在这道题中，我们对每条边的处理方法必须是相同的，也就是我处理到哪个节点之后下一个节点再交给下一条边取处理，这道题我们遵循每次处理第一个节点和最后一个节点的前一个节点，最后一个节点交给吓一条边来处理。

那处理一个 n 阶矩阵需要多少层呢？我们来看上下两个边，每次循环上下两个边未处理的部分会减少二，这样总共需要 n / 2 次就可以完全遍历完，但是如果是奇数的话会剩下中间那个未处理，因为我们是向下取整，这时候就在末尾再加一条语句来处理这个值。

所以我们外层写一个 while 循环控制遍历的圈数，总共遍历 n / 2 次内层写遍历的逻辑，每次循环四条边。

每次循环需要往里缩短一层，所以我们循环的起点和终点肯定不会写死的，这里构建一个 start 变量，和一个 end 变量，每次循环结束对这两个变量处理使得遍历的边向内移动。

我们先来写第一层遍历：

第一条边：起点设置为 start 中点为 n - end（倒数第二个节点），这是遍历的第 start 行的元素，设置循环变量为 j 遍历到倒数第二个节点。

第二条边：遍历的是一列，这里需要用到上面的 j ，这个 j 停止的地方就是我们下一次循环要遍历的列，这里设置一个 i 作为循环变量，一样是从 start 开始（每次向内推一层），同样遍历到 n - end 结束。

第三条边：这时候需要 i 的值，遍历的是第 i 行，遍历到 start + 1 也就是第二个元素

第四条边：同理，遍历的是第 j 列，遍历的终点仍然是 start + 1。

一层循环结束，更新 start 和 end 的值。

3.2 代码

class Solution {
    public int[][] generateMatrix(int n) {
        int index = 0;
        int loop = 0; // 控制循环次数，总共需要遍历 n / 2 次
        // n 阶矩阵
        int[][] res = new int[n][n];
        int start = 0;
        int i, j; // 因为遍历另一条边的时候需要前一条边的结束位置，需要保存
        int count = 1; // 这是每次填充的数字
        while(loop++ < n / 2) {
            for (j = start; j < n - loop; j++) {
                // 区间是左闭右开的不遍历最后一个元素
                res[start][j] = count++;
            }
            for (i = start; i < n - loop; i++) {
                res[i][j] = count++;
            }
            for (; j >= loop; j--) {
                res[i][j] = count++;
            }
            for (; i >= loop; i--) {
                res[i][j] = count++;
            }
            start++;
        }
        if (n % 2 == 1) {
            res[start][start] = count;
        }

        return res;
    }
}

3.3 简化

上面那个代码是我看了卡尔老师的代码更改的，上面舍弃了 end 的值，改为用 n - loop 也就是控制循环层数的那个值，因为这个值每次循环是进行了自增的，作用和 end 相同。

还有在第三条和第四条边那部分，没有采用 start + 1 的形式而是采用了 loop 原因也是每次循环中 loop 都会更新，而且更新是在 start 之前的，恰好满足了 start + 1 的需求（其实我感觉写 start + 1 更好理解）

然后就是最后这个更新操作，其实更新的就是中间的那个元素，写成 n / 2 也是对的，但我们发现出循环的时候，start 执行了自增，所以它处于的位置也是我们要处理的这个位置。