力扣区间题目：重叠、合并、插入、删除区间

一、汇总区间

---

题目描述： 给定一个 无重复 元素的 有序 整数数组 nums 。
返回恰好覆盖数组中所有数字的最小有序区间范围列表。也就是说，nums 的每个元素都恰好被某个区间范围所覆盖，并且不存在属于某个范围但不属于 nums 的数字 x 。
列表中的每个区间范围 [ a , b ] 应该按如下格式输出：(1)、“a->b” ，如果 a != b  (2)、 “a” ，如果 a == b
力扣：228. 汇总区间

输入：nums = [ 0 , 1 , 2 , 4 , 5 , 7 ]
输出：[“0->2”,“4->5”,“7”]
解释：区间范围是：
[0,2] --> “0->2”
[4,5] --> “4->5”
[7,7] --> “7”

题目分析： 通过示例，可以看出，区间是连续的，或者只有一个数两种情况，因为是有序的，在遍历的时候，如果 nums[i + 1] = nums[i] + 1 即可进行合并。

AC代码：

class Solution {
    public List<String> summaryRanges(int[] nums) {
        List<String> summary = new ArrayList<>();
        for (int i, j = 0; j < nums.length; ++j){
            i = j;
            while (j + 1 < nums.length && nums[j + 1] == nums[j] + 1)
                ++j;
            if (i == j) 
                summary.add(nums[i] + "");
            else
                summary.add(nums[i] + "->" + nums[j]);
        }
        return summary;
    }
}

二、合并区间

---

题目描述： 给出一个区间的集合，请合并所有重叠的区间。
力扣：56.合并区间

示例 1:
输入: intervals = [ [ 1 , 3 ] , [ 2 , 6 ] , [ 8 , 10] , [ 15 , 18] ]
输出: [ [ 1 , 6 ] , [ 8 , 10] , [ 15 , 18] ]
解释: 区间 [ 1 , 3 ] 和 [ 2 , 6 ] 重叠, 将它们合并为 [ 1 , 6 ] 。

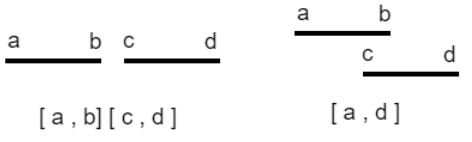
题目分析： 首先对区间按照起始端点进行升序排序，然后逐个判断当前区间是否与前一个区间重叠，如果不重叠的话将区间直接加入结果集，反之如果重叠，就将当前区间与前一个区间进行合并。因为已经是按照起始点进行升序排序，合并时只需比较两个区间的尾端点，保留最大值，获得新区间。
排完序后主要分两种情况，相互分离，包含重叠部分。

AC代码：

class Solution {
    public int[][] merge(int[][] intervals) {
        // 先按照区间起始位置排序
        Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]);
        // 遍历区间
        int[][] res = new int[intervals.length][2];
        int idx = -1;
        for (int[] interval: intervals) {
            // 如果结果数组是空的，或者当前区间的起始位置 > 结果数组中最后区间的终止位置，说明不重叠。
            // 则不合并，直接将当前区间加入结果数组。
            if (idx == -1 || interval[0] > res[idx][1]) {
                res[++idx] = interval;
            } else {
                // 反之说明重叠，则将当前区间合并至结果数组的最后区间
                res[idx][1] = Math.max(res[idx][1], interval[1]);
            }
        }
        return Arrays.copyOf(res, idx + 1);
    }
}

三、插入区间

---

题目描述： 给出一个无重叠的 ，按照区间起始端点排序的区间列表。
在列表中插入一个新的区间，你需要确保列表中的区间仍然有序且不重叠（如果有必要的话，可以合并区间）。
力扣： 57. 插入区间

输入：intervals = [ [ 1 , 2 ] , [ 3 , 5 ] , [ 6 , 7 ] , [ 8 , 10] , [ 12 , 16 ] ], newInterval = [ 4 , 8 ]
输出：[ [ 1 , 2 ] , [ 3 , 10 ] , [ 12 , 16 ] ]
解释：这是因为新的区间 [ 4 , 8 ] 与 [ 3 , 5 ] , [ 6 , 7 ] , [ 8 , 10 ] 重叠。

题目分析：
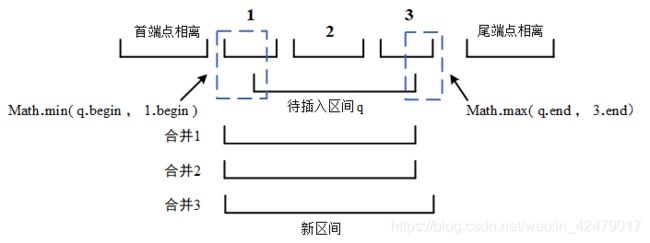
待插入区间，和给定的已知区间存在两种关系，相离 和 重叠 (首部重叠、完全重叠、尾部重叠)。
1、 首先将与待插入区间左边且相离的区间加入结果集，即判断待插入区间首端点，与当前区间尾端点之间的大小，如果待插入区间首端点 > 当前区间尾端点，即相离，可直接将当前区间加入结果集。
2、如果 待插入区间首端点 <= 当前区间尾端点 ，说明存在重叠，新区间的首端点可通过 Math.min(当前区间首端点 ， 待插入区间首端点) 获取 ，而尾结点即为 Math.max ( 当前区间尾段点 ， 待插入区间尾端点 ）最为新区间的尾端点。
3、最后即为与待插入区间尾端点相离的区间，即待插入区间尾端点 < 当前区间首端点 ，亦可直接将当前区间加入结果集。
汇总到一张图上有

AC代码：

class Solution {
    public int[][] insert(int[][] intervals, int[] newInterval) {
        int[][] res = new int[intervals.length + 1][2];
        int idx = 0;
        // 遍历区间列表
        // 1. 首先将与待插入区间，和当前区间首端点相离的，加入结果集
        int i = 0;
        while(i < intervals.length && intervals[i][1] < newInterval[0]){
            res[idx ++] = intervals[i ++];
        }
        // 2. 接下来判断与待插入区间重叠的，并进行合并，最终将合并的结果加入结果集
        while(i < intervals.length && intervals[i][0] <= newInterval[1]){
            newInterval[0] = Math.min(intervals[i][0] , newInterval[0]);
            newInterval[1] = Math.max(intervals[i][1] , newInterval[1]);
            i ++;
        }
        res[idx ++] = newInterval;
        // 3. 最后将新区间尾端点相离的区间加入结果集
        while(i < intervals.length){
            res[idx ++] = intervals[i ++];
        }
        // 因为存在重叠，所以最开始开的数组的长度可能比最终 res 中所包含的区间数小
        return Arrays.copyOf(res , idx);
    }
}

四、删除被覆盖区间

---

题目描述： 给你一个区间列表，请你删除列表中被其他区间所覆盖的区间。
只有当 c <= a 且 b <= d 时，我们才认为区间 [a,b) 被区间 [c,d) 覆盖。
在完成所有删除操作后，请你返回列表中剩余区间的数目。
力扣：1288. 删除被覆盖的区间

输入：intervals = [ [ 1 , 4 ] , [ 3 , 6 ] , [ 2 , 8 ] ]
输出：2
解释：区间 [ 3 , 6 ] 被区间 [ 2 , 8 ] 覆盖，所以它被删除了。

题目分析： 这里所说的覆盖是完全重叠关系，如 (三、插入区间) 上图中的区间2，(其中区间1 即为首端点重叠，而区间3 即为尾端点重叠) ， 而通过数据可以看出，原始的数组，区间是无序的，所以首先需要进行排序，先根据区间左端点升序，而当区间左端点相等时，则根据右端点降序。

AC代码：

class Solution {
    public int removeCoveredIntervals(int[][] intervals) {
        int len = intervals.length;
        // 特判
        if (len < 2) {
            return len;
        }
        // 特别注意：当区间左端点相同的时候，右端点降序排序
        Arrays.sort(intervals, (o1, o2) -> {
            if (o1[0] == o2[0]) {
                return o2[1] - o1[1];
            } else return o1[0] - o2[0];
        });
        // 需要被删除的区间个数
        int remove = 0;
        int currentRight = intervals[0][1];
        for (int i = 1; i < len; i++) {
            if (intervals[i][1] <= currentRight) {
                remove++;
            } else {
                currentRight = intervals[i][1];
            }
        }
        return len - remove;
    }
}

五、相似题目

---

1、力扣：435.无重叠区间 ，该题相对简单，只需要根据 尾端点 对区间进行升序排序即可，统计完全相离的区间个数，只要当前区间尾端点 <= 后一个区间首端点即认为相离，然后使用总区间个数减去相离个数，即为需要移除的个数。核心代码：

int count = 1;
int end = intervals[0][1];
for(int[] interval : intervals){
    if(end <= interval[0]){
        end = interval[1];
        count ++;
    }
}

2、力扣：452.用最少数量的箭引爆气球 ，该题和上面 435.无重叠区间一样，唯一的区别在于这里的边界必须满足严格的小于关系(存在擦边箭），即当前区间尾端点 < 后一个区间首端点，才使计数加 1 。