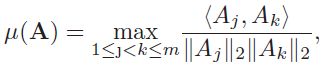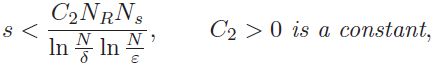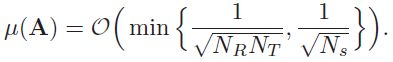论文解读--Compressed Sensing for MIMO Radar - Algorithms and Performance

MIMO雷达压缩感知-算法和性能

摘要

        压缩感知技术使得利用雷达场景的稀疏性来潜在地提高系统性能成为可能。本文将压缩感知工具应用于MIMO雷达，在方位-距离-多普勒域重构场景。推导了雷达波形和发射、接收阵列的条件，使雷达传感矩阵具有小相干性和稀疏恢复成为可能。提出了理论性能界限，并通过数值模拟进行了验证。

1 介绍

        雷达领域两个相对较新的发展是MIMO(多输入多输出)雷达的发展[9]，以及压缩感知在雷达信号处理中的应用[10]。

        MIMO雷达的特点是除了使用多个天线接收反射信号外，还使用多个天线同时发射各种通常正交的波形。MIMO雷达在提高空间分辨率和改善干扰和干扰抑制方面具有潜力。MIMO雷达能够根据接收到的数据调整发射波束，这在“传统”雷达中是不可能的。

        大多数雷达场景都是稀疏的，因为只有一小部分距离方位或距离多普方位角单元被感兴趣的目标占用。事实上，在大多数情况下，这个分数确实很小。这种稀疏性假设建议使用压缩感知(CS)框架来处理MIMO雷达问题[3,5]。本文发展了将CS应用于MIMO雷达所需的基本理论。关于压缩感知MIMO雷达波形设计的一些初步经验结果可以在[4]中找到。

       压缩感知的核心在于发现可以从待定线性方程组Ax = y精确地重建稀疏信号x，并且可以通过l1最小化以高效计算的方式完成，参见[2,3,5]。更具体地说，假设x∈Cm是一个稀疏的信号，即其非零分量的个数满足 (其中)。考虑到Ax = y，其中A是一个秩为n且n < m的n×m矩阵。由于这个系统是待定的，所以有无穷多个解。由于x的稀疏性我们可以通过求解优化问题来计算x

          (1)

        然而，求解(1)是NP-hard问题，因此实际上是不可行的。相反，我们考虑它的凸松弛(也称为基寻迹)

          (2)

        这可以通过线性或二次规划技术有效地解决。现在我们知道，在矩阵A和x的稀疏性的一定条件下，(1)和(2)具有相同的唯一解[2,3,5,6]。其中一个条件是受限等距性[2]，它可以由高斯随机矩阵或随机偏傅立叶矩阵来满足。另一个条件(本文使用的)是基于A的(in)相干性，定义为

          （3）

        其中Ai表示A的第i列，见[6,14]。在[12]中可以找到一些小相干矩阵的例子。

        在雷达设置中，传感矩阵A代表一个物理过程(电磁波的散射)，因此我们不能简单地选择A为高斯随机矩阵或随机偏傅立叶矩阵。然而，某些参数是我们可以控制的，例如雷达发射信号的选择，以及发射和接收天线的位置。因此，分析是否以及如何选择我们控制的参数使MIMO雷达传感矩阵具有较小的相干性是至关重要的。

2 信号模型

        考虑在发射机上使用NT个天线，在接收机上使用NR个天线的MIMO雷达。我们假设阵元间距足够小，使得给定散射体的雷达回波在整个阵列上完全相关。换句话说，这是一个相干的传播场景。

       为了简化演示，我们假设两个阵列位于同一位置，即这是一个单静态雷达。只要每个阵列的相干性假设成立，双静态情况的扩展就很简单。阵列由阵列集合表征:接收阵列为aR(θ)，发射阵列为aT (θ)，其中θ为相对于阵列的方向。我们假设阵列和所有散射体都在同一个二维平面上。对三维情况的扩展很简单，下面所有的结果也适用于三维情况。

        让Z (t;θ,r)为单位强度目标在θ方向和r距离上的无噪声接收信号矩阵NR ×Ns，其中Ns为时域采样个数。然后

          (4)

        式中，τ = 2r/c，其中c表示光速，S(t−τ)为NT × Ns矩阵，其行为循环延迟信号si(t−τ)。第i个发射天线发射si(t)，其中t = 1，···，Ns。

        假设等间距线性阵列(ULA)，阵列集合为

          (5)

       和

          (6)

        其中dT和dR分别是发射和接收阵列阵元之间的归一化间隔(距离除以波长)。

        已知MIMO雷达的空间特性与具有NT*NR天线的虚拟阵列密切相关，其阵列集合为a(θ) = aT (θ)⊗aR(θ)。我们知道[8]，如果选择发射阵列和接收阵列的间距，可以得到均匀间隔的半波长间隔的虚拟阵列:

          (7)

          (8)

        这两种选择都会生成孔径为0.5(NT*NR−1)波长的虚拟阵列。这是无栅瓣的最大虚拟孔径。选项(7)和(8)也将再次出现在我们的理论分析中，参见定理1。

        下面令为无噪声矢量化接收信号。建立离散距离方位网格{(θi, rj)}， 1≤i≤Nθ， 1≤j≤Nr，其中Δθ和Δr表示相应的离散步长。利用向量z(t;θ,r)对于所有网格点(θi, rj)，我们构造一个完备的响应矩阵A，其列为z(t;θi, rj)，1≤i≤Nθ、1≤j≤Nr。换句话说，我们有Nr个距离值和Nθ个方位角值，因此A是NRNs × NrNθ矩阵。

        假设雷达辐射由K个散射体组成的场景，这些散射体位于(θi, rj)网格的K个点上。设x为稀疏向量，其非零元素为场景中散射体的复振幅。零元素对应于没有被散射体占用的网格点。然后我们可以定义从这个场景接收到的雷达信号

        y = Ax + v  (9)

        其中，y为NRNs×1向量，x为NrNθ ×1稀疏向量，v为NRNs×1复高斯噪声向量，A为NRNs× NrNθ矩阵。

        到目前为止的讨论是针对静态雷达场景和固定雷达的情况，在这种情况下不存在多普勒频移。将该信号模型扩展到包括多普勒效应在概念上是简单的，但会导致问题维度的显著增加。

        单位强度散射体在θ方向，距离r和多普勒fd(对应于其相对于雷达的径向速度)的回波信号模型由下式给出

          (10)

        式中τ = 2r/c，其中c表示光速，S(t−τ)为NT × Ns矩阵，其行为循环延迟和多普勒频移信号si(t−τ) 。

        和之前一样，让z(t;θ,r, fd) = Z(t;θ,r, fd)为无噪声矢量化接收信号。我们通过增加一个离散的多普勒分量(步长Δf和相应的Nf多普勒值)来扩展离散的距离-方位网格，得到一个均匀的距离-方位-多普勒网格{(θi, rj, fk)}。对于所有离散(θi, rj, fk)，利用向量z(t;θ,r,fd)我们构造一个完备响应矩阵A，其列为z(t;θi, rj, fk)，1≤i≤Nθ、1≤j≤Nr, 1≤k≤Nf。

        假设雷达辐射由K个散射体组成的场景，这些散射体位于(θi, rj, fk)网格的K个点上。设x为稀疏向量，其非零元素为场景中散射体的复振幅。零元素对应于没有被散射体占用的网格点。然后我们可以定义从这个场景接收到的雷达信号

        y = Ax + v  (11)

        其中，y为NRNs×1向量，x为NrNθNf ×1稀疏向量，v为NRNs×1复高斯噪声向量，a为NRNs× NrNθNf矩阵。

3 理论结果

       系统(11)是否欠定取决于参数Δθ，Δr，Δf的选择。显然，我们总是可以选择一个非常粗糙的雷达场景离散化，以这种方式确保(11)是超定的。但由于我们的目标是在范围、方位和多普勒上获得高分辨率，这不是可行的方法。然而，当我们增加分辨率时(通过使Δθ，Δr，Δf变小)，我们增加了A的列数，线性系统Ax = y变得越来越不确定。同时，A的相干性变得更差，因为A的相邻列看起来越来越相似。最终μ(A)会变得太大，基寻迹会失败。因此，我们在这里面临着一个基本的权衡，关键是在最大分辨率和确保矩阵A仍然满足基寻迹成功的条件之间找到平衡。

       下面的定理对我们所推导出的理论结果的类型有了初步的了解。它解决了无噪声静态雷达场景的情况。类似的，但稍微复杂一点的定理适用于多普勒情况。

       定理1假设我们有NT个发射天线和NR个接收天线，其对应的阵列集合由式(5)和式(6)给出。进一步假设我们从每个发射天线发送的AWGN信号长度为Ns。选择dR =1/2, dT = 1/2NR或dR =1/2NT, dT =1/2，令−π/4≤θ≤π/4，设Δτ = c/2B(其中c为光速，B为信号带宽)，Δθ = 2/NRNT。令N:= max{NRNT,Ns}，令ε，δ > 0。则s均匀分布在随机分布的目标上，其稀疏度可达

         (12)

       可以通过基寻迹以高概率(取决于ε，δ)恢复。

        这个证明太长了，不能包括在这里，将在即将发表的论文中提出。证明的关键思想是证明A的相干性很小，然后应用[14]中的定理B和定理14。关于A的相干性我们证明了

          (13)

        为了获得相干性(13)，需要根据定理选择dR、dT和Δθ的值。实际上，这些选择与图1中显示的波束方向图密切相关。

        在有噪声的情况下，我们可以用下式代替(2)

          （14）

        或用等效的Lasso[13]

          (15)

        通过将我们对A的相干估计与[1]中的定理1.2相结合，使用(15)而不是(2)可以推导出定理1的“噪声”模拟。

        我们的数值模拟也表明，似乎可以去掉定理1中目标必须随机分布的要求。

4 数值结果

        为了说明压缩感知MIMO雷达的性能，我们在这里给出几个“玩具”示例。更完整的性能评估超出了本文的范围，将在即将发表的论文中提出。在这些示例中，我们使用NT = NR = 10个阵元的发送和接收阵列，间距为dR = 0.5, dT = 0.5NR。方位角距离样本个数为Nθ = 30, Ns = Nr = 30。

        图1描绘了虚拟阵列的波束图，可以看到它具有1度的3dB波束宽度，与阵列孔径0.5NTNR的倒数密切匹配。从零到零的主瓣宽度为2.3度。该阵列在压缩感知雷达中不明显出现，但其波束方向图与A的可实现相干性有关，因此提供了该雷达系统预期空间分辨率的指示。

图1 虚拟阵列波束方向图，NT=NR=10阵元，dR = 0.5, dT = 0.5NR间距，未加窗

        图2描绘了一个由13个单位振幅散射体以特定几何排列组成的雷达场景。注意，在本例中，目标不是随机分布的。标题为X的子图显示了无噪声雷达场景。标题为的子图显示了使用上述压缩感知算法估计的场景，使用噪声标准差σ = 3的噪声数据。第三个子图显示了使用匹配过滤器Xmf估计的场景，以供参考。更准确地说，Xmf是向量Xmf的重塑版本，

          (16)

        其中W为匹配的滤波矩阵，其列为归一化为单位范数的A的列。

图2 一个具有13个散射体的雷达场景X，使用压缩感知算法和使用匹配滤波器Xmf来估计场景。

        图3描绘了一个由25个随机放置的散射体组成的雷达场景，其振幅随机分布在0到1之间。标题为X的子图显示了无噪声雷达场景。标题为的子图显示了使用上述压缩感知算法估计的场景，使用噪声标准差σ = 3的噪声数据。第三个子图显示了使用匹配过滤器Xmf估计的场景，以供参考。

图3 一个随机雷达场景X有25个散射体，估计场景使用压缩感知算法和使用匹配的滤波器Xmf。

        接下来，我们通过实验研究了压缩感知算法失效的稀疏度水平。如定理1所示，x的可容许稀疏度s的上界大致为0 (NRNs/ lnN)。我们对给定数量的散射体生成随机的无噪声雷达场景，并计算这些随机场景的估计误差的平均值。估计误差定义为X−的Frobenius范数。在不同的s值下重复实验，结果如图4所示。注意，当s < 106时，误差很小，当s大于106时，误差迅速增大（备注：因此不能用于车载雷达多目标场景）。这种行为与众所周知的高斯矩阵和其他压缩感知矩阵的相变现象一致[7]。

图4 不同数量散射体s的平均估计误差

5 结论

        我们提出了一个初步的理论和数值框架来利用MIMO雷达的雷达场景稀疏性。根据压缩感知的结果，给出了可实现的距离、方位分辨率和可恢复目标数量的界限。我们的理论和数值研究结果表明，在MIMO雷达中使用稀疏表示和压缩感知工具具有很大的潜力。