初识C语言·递归

1 什么是递归

2 递归的限制条件

3 递归举例

4 递归与迭代

---

1 

递归，这两字的理解应该分开来理解，递推和回归，在C语言中，递归是函数自己调用自己，最后返回一个结果，比如写一段最简单的递归。

int main()
{
	main();
	return 0;
}

main()函数自己调用自己，调用的main函数里面又有一个main函数，就这样无限调用，这就是一个递归，但是最后会栈溢出的，因为这串代码结束不了，没有停止的条件，所以，递归想要结束是需要限制条件的，至于为什么会栈溢出呢？笔者的看法是内存在栈区为main函数开辟函数栈帧，无限开辟会导致栈区的空间不足，所以会栈溢出。

使用递归前，我们应该知道，递归的思想是：大事化小。

---

2 

上文提及到了，递归如果想要结束就需要限制条件，否则就会一直执行下去。

那么递归的限制条件就是

1）递归的时候应该有限制条件

2）每次递归的时候都应该越来越接近这个限制条件

---

3

好了，递归的基本内容就那么多，直接举例咯

1）递归实现n的阶乘

先看看不用递归实现阶乘

int main()
{
	int num = 0, ret = 1;
	scanf("%d", &num);
	for (int i = 1; i <= num; i++)
	{
		ret *= i;
	}
	printf("%d", ret);
	return 0;
}

那么，如何使用递归实现阶乘呢？

我们知道，阶乘是给一个数，从1 开始乘，乘到这个数，那么问题可不可以简化成一个数乘比自己小1的数，小1的那个数再乘比自己小1的数呢？我看行，那么限制条件呢？限制条件应该是这个数每次减1都应接近于1，为1的时候就返回1，结束程序。

来吧，实现。

int Fac(int num)
{
	if (1 == num)
	{
		return 1;
	}
	else
	{
		return num * Fac(num - 1);
	}
}
int main()
{
	int num = 0;
	scanf("%d", &num);
	int ret = Fac(num);
	printf("%d\n", ret);
	return 0;
}

哦吼，对辣！但是，你说会不会溢出呢？毕竟这是阶乘，到后面大的离谱。

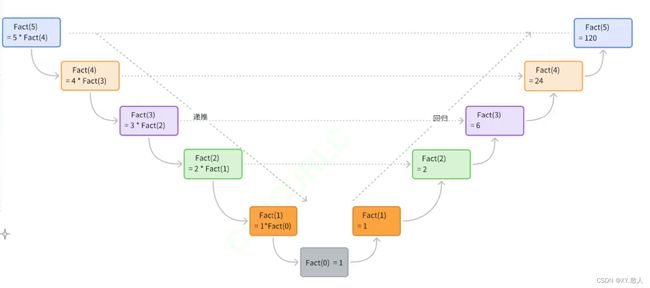
还没理解？看看这张图呢？

所以测试的时候别太离谱就行。

2)递归实现斐波那契数列

斐波那契数列知道吧？对，是个数列（废话文学）。

1 1 2 3 5 8 13 21 ……这样的，前两个元素是1，且从第三项开始任意一项都等于前两项相加的，就被称为斐波那契数列。那么我们现在要做的是，输入任意一个数，求这项的值。

还是先不用递归写一次。

int main()
{
	int a = 0, b = 1, c = 1;
	int n = 0;
	scanf("%d", &n);
	while (n)
	{
		c = a + b;
		a = b;
		b = c;
		n--;
	}
	printf("%d", a);
	return 0;
}

这个是没有问题的，至于为什么打印a，为什么a = 0,b = 1.c = 1开始，就交给读者实验了。

现在，就用递归来实现。

前面已经解释了，任意一项是由前两项相加而来，就可以开始写了。

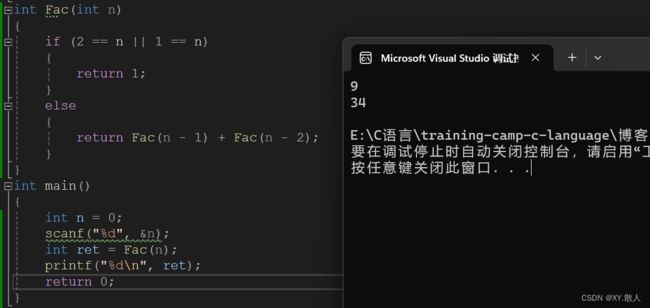
int Fac(int n)
{
	if (2 == n || 1 == n)
	{
		return 1;
	}
	else
	{
		return Fac(n - 1) + Fac(n - 2);
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fac(n);
	printf("%d\n", ret);
	return 0;
}

当然，限制条件也可以写n < 3。都一样的。

3）递归实现打印数字的每一位

比如输入一个数，1234，那么打印出来的就是1 2 3 4。同样，还是先不用递归打印。

int main()
{
	int num = 0,count = 0,a = 1;
	scanf("%d", &num);
	int n = num;//创建一个变量方便一会整除
	while (num)//先确定有多少位
	{
		count++;
		num /= 10;
	}
	int m = count;//创建一个变量方便一会儿整除
	while (count)
	{
		int t = (int)pow(10, m - 1);
		printf("%d ", (n / t) % 10);
		m--, count--;
	}
	return 0;
}

当然了，该有的头文件不要省略了，比如math头文件，，

现在尝试用递归实现。

void Print(int num)
{
	if (num > 0)
	{
		Print(num / 10);
		printf("%d ", num % 10);
	}
}
int main()
{
	int num = 0;
	scanf("%d", &num);
	Print(num);
	return 0;
}

可能有点难以理解，我们要从最高位开始打印，所以真正打印的时候，是从1开始的，那么在即将满足限制条件的时候，我们就开始回归，进行打印。

---

4

举例就3个，倘若你认为不过瘾，我推荐你可以去了解一下递归应用在实际生活的问题，比如汉诺塔问题和青蛙跳台阶的问题。

现在介绍一下递归和迭代，它们是有差异的。

递归，就是在运行的过程中调用自己。
迭代法也称辗转法，是一种不断用变量的旧值递推新值的过程，跟迭代法相对应的是直接法(或者称为一次解法)，即一次性解决问题。

比如上文中不用递归实现的阶乘 / 斐波那契的写法就是迭代写法。

先介绍阶乘，如迭代一样，它是一次性计算完结果的，不用像递归一样，分好几次调用，

同理，斐波那契数列也是一样的，迭代的效率确实比递归快

当然，文字叙述你是感觉不到差异的，实际代码操作一下你就知道了。

int count = 0;
int Fac(int n)
{
	if (3 == n)
	{
		count++;
	}
	if (n < 3)
	{
		return 1;
	}
	else
	{
		return Fac(n - 1) + Fac(n - 2);
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fac(n);
	printf("%d\n", count);
	printf("%d\n", ret);
	return 0;
}

我们求第40项的值的时候，我们顺便求一下第三项的值会被用多少次。答案是39088139次，恐怖吧？

我们也可以使用计时工具,clock来直观比较一下他们的时间运行差异，你看，这差异是近6倍的时间差异了。

而且，每次调用递归的时候，也就是调用函数了，内存里面会为这个函数单独开辟一块空间，也就是说你这个程序没有结束，那么空间会一直开辟下去，所以理论上来讲，即便是一个合理的程序，只要递归的次数足够多，是可以导致栈溢出的。

当然了，存在即合理，递归有自己的用处，但是对于这些计算什么的，可以多考虑使用迭代。

---

感谢阅读！