傅里叶变换的性质之二维DFT的平移性和旋转性——冈萨雷斯数字图像处理
平移性原理
基本概念:
平移性指的是函数在空间域内平移时,其频率域表示也相应改变的性质。
在二维DFT中,当一个图像在空间域内平移时,其频率域表示(即DFT)的振幅不会改变,但相位会改变。
数学表达

直观理解:
平移一个图像不会改变其频率内容,只会改变每个频率成分的相位。
旋转性原理*
基本概念:
旋转性指的是当一个图像在空间域内旋转时,其频率域表示也相应地旋转同样的角度。这意味着频率域的结构在旋转操作下保持不变。
数学表达:

直观理解:
在频率域内,旋转图像等同于以原点为中心旋转其频谱。
*要求:
实现图像的平移和旋转;计算图像的傅里叶频谱图。
python代码实现
import cv2
import matplotlib.pyplot as plt
import numpy as np
img=cv2.imread("Fig0424.tif",0)
rows, cols = img.shape[0:2]
M = np.float32([[1, 0, 100], [0, 1, 50]])
dst = cv2.warpAffine(img, M, (cols, rows))#平移
M1=cv2.getRotationMatrix2D((cols/2,rows/2),135,1)
dst1=cv2.warpAffine(img,M1,(cols,rows)) #旋转
dft = np.abs(np.fft.fft2(img))
log_dft = np.log(1+dft)
center_dft = np.fft.fftshift(log_dft)
dft1 = np.abs(np.fft.fft2(dst))
log_dft1 = np.log(1+dft1)
center_dft1 = np.fft.fftshift(log_dft1)
dft2 = np.abs(np.fft.fft2(dst1))
log_dft2 = np.log(1+dft2)
center_dft2 = np.fft.fftshift(log_dft2)
plt.subplot(321),plt.imshow(img,"gray"),plt.title("orginal")
plt.subplot(322),plt.imshow(center_dft,"gray"),plt.title("DFT")
plt.subplot(323),plt.imshow(dst,"gray"),plt.title("translated")
plt.subplot(324),plt.imshow(center_dft1,"gray"),plt.title("translated DFT")
plt.subplot(325),plt.imshow(dst1,"gray"),plt.title("rotated")
plt.subplot(326),plt.imshow(center_dft2,"gray"),plt.title("rotated DFT")
plt.show()
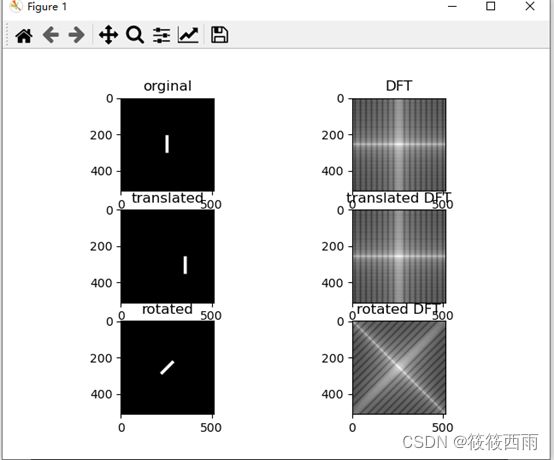
结果展示
结论
首先Numpy 进行傅里叶变换。Numpy 中的 FFT 包可以帮助我们实现快速傅里叶变换。函数 np.fft.fft2() 可以对信号进行频率转换,输出结果是一个复杂的数组。本函数的第一个参数是输入图像,要求是灰度格式。第二个参数是可选的, 决定输出数组的大小。输出数组的大小和输入图像大小一样。如果输出结果比输入图像大,输入图像就需要在进行 FFT 前补0。如果输出结果比输入图像小的话,输入图像就会被切割。
图像的平移并不会影响图像的频谱,同时,图像的相位会随着图像的旋转而旋转,而且这个实验表明矩形的平移并不会对频谱有丝毫的影响,而频谱随着矩形的旋转而旋转相同的角度。