力扣189 - 轮转数组【空间换时间、三步翻转法】

一、题目描述

原题传送门

给你一个数组，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1：

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2：

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

• 本题的题目思路很简单，就是给你一个数组，然后将这个数组中后k个数字一一翻转到前面来，最后得到的就是向右轮转后的数组
• 本题比上一题复杂一些，有一些边界值需要考虑，【因此建议大家画图】

三、方法1：直接翻转移动【超时】

• 外层的while循环执行的是k的翻转次数，内层的for循环实现的是逐步的移位操作，因此时间复杂度为O(k * numsSize)，若是这个k == numsSize，那么时间复杂度将会到达O(N²)，在力扣上O(N²)的时间复杂度是很容易超时的，所以不建议大家使用此方法

//超时
while(k--)
{
    int ret = nums[numsSize - 1];
    for(int i = numsSize - 1;i > 0; i--)
        nums[i] = nums[i - 1];
    nums[0] = ret;
}

三、方法2：空间换时间【C语言】

1、思路分析

首先第一个思路是使用空间换时间的思想，也就是将每次移动的数字放入另一个数组，最后拷贝回来

• 讲一下整体的思路，首先你需要一个数组，去存放临时放置的数字
• 然后要将后k个数字移动到前面
• 其次将n - k个数字移动到后面
• 最后将移动完的数组再拷贝绘原数组

2、整体代码展示

我们来看一下代码

void rotate(int* nums, int numsSize, int k){
    int n = numsSize;
    int tmp[n];      //变长数组【C99】

    //1.首先对k做一个取模操作，防止数组访问越界
    k %= n;
    //2.将后k个数字移动到前面
    int j = 0;
    for(int i = n - k;i < n; ++i)
       tmp[j++] = nums[i]; 

    //3.n - k个数字移动到后面
    for(int i = 0;i < n - k; ++i)
        tmp[j++] = nums[i];

    //4.将移动完的数组再拷贝绘原数组
    for(int z = 0;z < n;++z)
        nums[z] = tmp[z];
}

力扣提交结果
很明显，内存消耗比较多，因为需要维护一个临时数组

3、代码详解

然后我们对这段代码来详细讲解一下

• 首先我们需要一个临时放置的数组，因此开辟一个变长数组，这个在力扣上应该是可以过的，C99新出的特性，C89不支持，可能在VS这样的编译器上会报错
• 然后我们先跳过取余的这一段逻辑，看下面
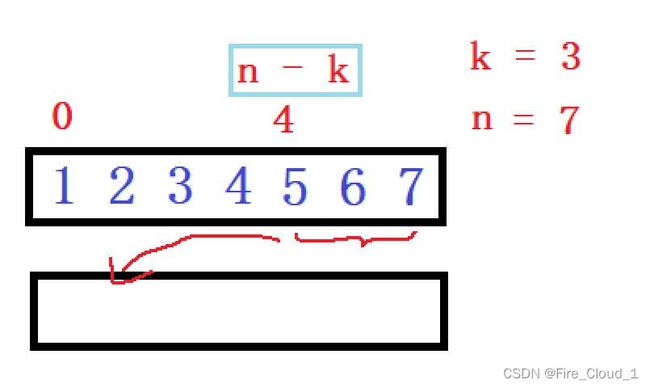
• 首先就是要将后k个数字移动到前面，我们通过图示来看一下

• 可以看到，我们需要移动的是5~7这三个数组，此时你应该通过题目已经给出的n和k去判断边界值，5所在的位置是下标4,7所在的位置是n - 1,7后面就是n，这个时候需要你去联想一下通过下面的几个案例算一下，其实就可以发现后面需要翻转的初始位置应该是【n - k】
• 然后对于循环的边界我们最好是写成左闭右开的形式，所以【< n】即可

//1.首先对k做一个取模操作，防止数组访问越界
k %= n;
//2.将后k个数字移动到前面
int j = 0;
for(int i = n - k;i < n; ++i)
   tmp[j++] = nums[i]; 

---

• 然后第二步，我们要将前n - k个数字移动到后面
• 这个时候就体现出画图的重要性的，从下图可以看出，当后k个数字移动到赋值到临时数组中时，这个递增变量j也就刚好移动到了临时数组此时需要开始放置的起始位置，因此我们只需要考虑拷贝那一段便可

• 很明显可以知晓，前n - k个数字从0开始，边界值就是n - k - 1，使用左闭右开的形式来写【< n - k】即可

//3.n - k个数字移动到后面
for(int i = 0;i < n - k; ++i)
    tmp[j++] = nums[i];

• 当临时数组中已经存放好了需要翻转的数字后，我们将临时数组中的数字全部拷贝会原数组即可

//4.将移动完的数组再拷贝绘原数组
for(int z = 0;z < n;++z)
    nums[z] = tmp[z];

---

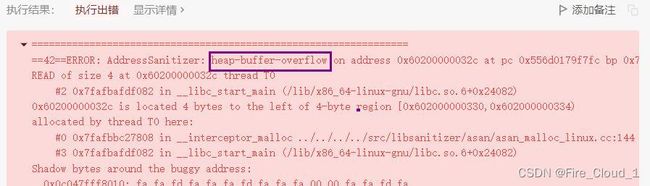
但是你会发现，就这样提交会出现执行出错，会出现一个溢出的情况，这是为什么呢？这个时候就需要使用到我开头跳过的那句代码

//1.首先对k做一个取模操作，防止数组访问越界
k %= n;

• 假设k = 3，n = 7,那就是我们例子中的翻转
• 假设k = 7，n = 7,形成的是一个整体翻转
• 假设k = 8，n = 7,此时需要翻转的数字个数大于题目给出的数字个数，其实翻转8次就是翻转1次，对应了我们题目中的【轮】这个字眼，也就是一轮满了，需要重新开启第二轮，那这个时候就需要使用到取余【%】这么一个操作

• 此时你再去提交，就发现没什么问题＜（＾－＾）＞

四、方法3：三步翻转法【C++】

1、思路分析

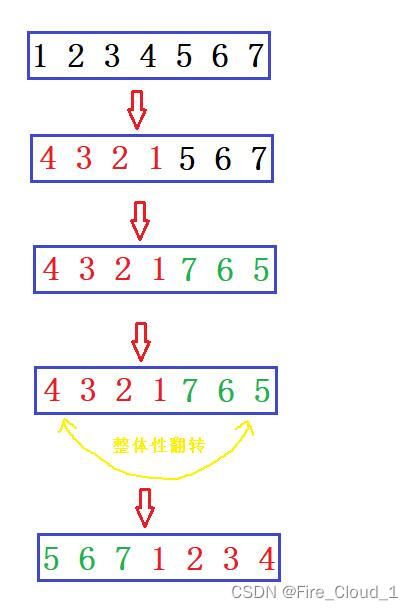
接下来再介绍一种比较巧妙的办法，就是【三步翻转法】

• 整体的思路就是现将前n - k个数字做一个翻转，然后将后k字数字做一个反转，最后将整个数组做一个翻转，思路很简单，但是不容易想到

2、整体代码展示

先看一下整体的代码

class Solution {
private:
    void trans(vector<int>&nums, int begin, int end)
    {
        for(int i = begin, j = end; i <= j; ++i, --j)
            swap(nums[i],nums[j]);
    }
public:
    void rotate(vector<int>& nums, int k) {
    int n = nums.size();
    k %= n;
    //1.首先将前n-k个数字翻转
    trans(nums, 0, n - k - 1);

    //2.然后将后k个数字翻转
    trans(nums, n - k, n - 1);
        
    //3.最后将整体做一个翻转
    trans(nums, 0, n - 1);
    }
};

力扣提交结果
可以看出，整体的效率较新开辟一个临时数组来的高效一些

3、代码详解

来分析一下代码

• 首先需要将翻转的逻辑封装成一个函数，使用双指针的思路，做一个前后翻转即可，这个我们之前做字符串翻转的题目里也有讲到过

void trans(vector<int>&nums, int begin, int end)
{
    for(int i = begin, j = end; i <= j; ++i, --j)
        swap(nums[i],nums[j]);
}

• 然后在主接口也是一样，需要先对这个k进行一个取余的操作，保证数组不会访问越界
• 接下去就是三次翻转，我写的非常清晰，只需要传入边界值给到封装好的函数即可
• 对于边界值的判断，非常重要，这一点我不细讲。希望你可以自己去试着画画图，对题目的理解也是有很好的帮助，下面给到流程图参考一下

五、总结与提炼

• 本文我们主要是讲解了一道力扣题，叫做【轮转数组】，面对题目给出的数组和k，需要将后k个数字翻转到前面特别要注意的是这个k可能会大于数组的长度，所以需要进行一个取余的操作
• 在本文中，主要是给出了三种解法【直接翻转移动】、【空间换时间】、【三步翻转法】，对于第一种方法不建议，复杂度较高，易超时，第二种空间换时间的思路大家应该都可以想到，但是效率不高，最后一种三步翻转法比较巧妙，整体的效率也比较高一些，重点掌握

以上就是本文的所有内容，如有问题请于评论区留言或者私信我，感谢您对本文的观看