LeetCode-题目详解(一):数组
这里写目录标题
-
- 1. 两数之和 【简单】
- 剑指 Offer 03. 数组中重复的数字 【简单】
- 45. 跳跃游戏 II 【中等】
- 48. 旋转图像
- 15. 三数之和 【中等】
- 53. 最大子数组和 【简单】
- 88. 合并两个有序数组 【简单】
- 54-螺旋矩阵【剑指 Offer 29. 顺时针打印矩阵】
- 剑指OfferII074-合并区间
- 31. 下一个排列 【中等】
- 118. 杨辉三角 【简单】
- 16. 最接近的三数之和 【中等】
- 55. 跳跃游戏 【中等】
- 283. 移动零 【简单】
- 59. 螺旋矩阵 II
-
- 方法一:按层模拟
- 118. 杨辉三角
- 867. 转置矩阵
- 面试题 01.08. 零矩阵
- 189. 轮转数组
- 238. 除自身以外数组的乘积【剑指 Offer 66. 构建乘积数组】
1. 两数之和 【简单】
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
- 2 <= nums.length <= 103
- -109 <= nums[i] <= 109
- -109 <= target <= 109
- 只会存在一个有效答案
方法一:暴力枚举【 O ( N 2 ) O(N^2) O(N2),其中 N 是数组中的元素数量】
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
n = len(nums)
for i in range(n):
for j in range(i + 1, n):
if nums[i] + nums[j] == target:
return [i, j]
return []
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
vector<int> ilist;
int n = nums.size();
for(int i = 0; i < n; i++){
for(int j= i + 1; j < n; j++){
if (nums[i] + nums[j] == target){
ilist.push_back(i);
ilist.push_back(j);
}
}
}
return ilist;
}
};
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int n = nums.size();
for(int i = 0; i < n; i++){
for(int j = i + 1; j < n; j++){
if(nums[i] + nums[j] == target){
return {i, j};
}
}
}
return {};
}
};
方法二:哈希表【O(N),其中 N 是数组中的元素数量】
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
hashmap={}
for ind,num in enumerate(nums):
hashmap[num] = ind
for i,num in enumerate(nums):
j = hashmap.get(target - num)
if j is not None and i!=j:
return [i,j]
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
vector<int> ilist;
map<int, int> hashmap;
for(int i = 0; i < nums.size(); i++){
hashmap[nums[i]] = i;
}
for(int i = 0; i < nums.size(); i++){
if(hashmap.find(target - nums[i]) != hashmap.end()){
int j = hashmap[target - nums[i]];
if(i != j){
ilist.push_back(i);
ilist.push_back(j);
return ilist;
}
}
}
return ilist;
}
};
方法三:哈希表【O(N),其中 N 是数组中的元素数量】
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
hashtable = dict()
for i, num in enumerate(nums):
if target - num in hashtable:
return [hashtable[target - num], i]
hashtable[nums[i]] = i
return []
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> hashtable;
for(int i = 0; i < nums.size(); i++){
auto it = hashtable.find(target - nums[i]); // hashtable的迭代器
if(it != hashtable.end()){ // 如果找到元素
return {i, it->second};
}
hashtable[nums[i]] = i; // 将键值对放入hashtable中
}
return {};
}
};
剑指 Offer 03. 数组中重复的数字 【简单】
找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
示例 1:
输入:
[2, 3, 1, 0, 2, 5, 3]
输出:2 或 3
限制:2 <= n <= 100000
方法一:哈希表 / Set【 O(N) : 遍历数组使用 O(N) ,HashSet 添加与查找元素皆为 O(1)】
class Solution:
def findRepeatNumber(self, nums: [int]) -> int:
my_set = set()
for num in nums:
if num in my_set:
return num
my_set.add(num)
return -1
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
unordered_map<int, int> hashtable;
for(int i = 0; i < nums.size(); i++){
auto it = hashtable.find(nums[i]);
if(it != hashtable.end()){
return nums[i];
}
hashtable[nums[i]] = i;
}
return 0;
}
};
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
unordered_map<int, int> hashtable;
for(int num : nums){
auto it = hashtable.find(num);
if(it != hashtable.end()){
return num;
}
hashtable[num] = 1;
}
return 0;
}
};
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
unordered_map<int, bool> hashtable;
for(int num : nums){
std::cout << "num = " << num << "; hashtable[num] = " << hashtable[num] << std::endl;
if(hashtable[num]){
return num;
}
hashtable[num] = true;
}
return 0;
}
};
num = 2; hashtable[num] = 0
num = 3; hashtable[num] = 0
num = 1; hashtable[num] = 0
num = 0; hashtable[num] = 0
num = 2; hashtable[num] = 1
45. 跳跃游戏 II 【中等】
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。
示例 1:
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: [2,3,0,1,4]
输出: 2
提示:
- 1 <= nums.length <= 1000
- 0 < = n u m s [ i ] < = 1 0 5 0 <= nums[i] <= 10^5 0<=nums[i]<=105
class Solution:
def jump(self, nums: List[int]) -> int:
n=len(nums)
if n==1:return 0
# cur:当前跳的活动范围
# nex:下一跳的最远距离
# step:到达最后位置的最少步数
cur,nex,step=0,0,0
for i,num in enumerate(nums):
nex=max(nex,i+num)
if nex>=n-1:
return step+1
if i==cur:
cur=nex
step+=1
方法二:贪心算法
class Solution:
def jump(self, nums: List[int]) -> int:
n = len(nums)
if n < 2:
return 0
step = 0 # 需要走的步数
cur_can_right = 0 # 下一步覆盖最远下标【当前往右跳的最远位置】
nxt_start = 0 # 当前覆盖的最远坐标,下一次的起点(临界点,必须要再往右跳的点)
for i in range(n - 1):
cur_can_right = max(cur_can_right ,i + nums[i]) # 更新下一步覆盖最远距离下标
if i == nxt_start : # 如果当前覆盖最远距离下标不是终点【到了临界点了,必须再往右跳】
nxt_start = cur_can_right # 更新当前覆盖最远距离下标(相当于加油了)【往右跳,使劲跳】
step += 1 # 需要走下一步
return step
方法二:动态规划
- 首先初始化DP数组,默认不跳,每个格子的走的次数就是它的下标
- 每到一个格子,更新它所有能到的格子的下标,如果比原来存储的少,则替换
class Solution(object):
def jump(self, nums):
dp = [i for i in range(len(nums))] # 初始化dp数组【dp[i]表示从0跳到i的最小跳数】
print("初始化:dp = ", dp)
print("===========================================================")
for i in range(len(nums)):
# temp =i(现在位置的坐标)+nums[i](能飞的最大距离)
furthest = i + nums[i]
# 每个位置更新一遍
for j in range(i, furthest + 1): # 遍历在位置i到能跳到的最远处furthest之间的所有位置
if j < len(nums):
print("i = {0}--furthest = {1}--j = {2}--dp[i] + 1 = dp[{0}] + 1 = {3}--dp[j] = dp[{2}] = {4}".format(i, furthest, j, dp[i] + 1, dp[j]))
dp[j] = min(dp[j], dp[i] + 1)
print("更新:dp = ", dp, "\n")
return dp[-1]
solution = Solution()
nums = [2, 3, 1, 1, 4]
result = solution.jump(nums)
print("result = ", result)
输出结果:
初始化:dp = [0, 1, 2, 3, 4]
===========================================================
i = 0--furthest = 2--j = 0--dp[i] + 1 = dp[0] + 1 = 1--dp[j] = dp[0] = 0
更新:dp = [0, 1, 2, 3, 4]
i = 0--furthest = 2--j = 1--dp[i] + 1 = dp[0] + 1 = 1--dp[j] = dp[1] = 1
更新:dp = [0, 1, 2, 3, 4]
i = 0--furthest = 2--j = 2--dp[i] + 1 = dp[0] + 1 = 1--dp[j] = dp[2] = 2
更新:dp = [0, 1, 1, 3, 4]
i = 1--furthest = 4--j = 1--dp[i] + 1 = dp[1] + 1 = 2--dp[j] = dp[1] = 1
更新:dp = [0, 1, 1, 3, 4]
i = 1--furthest = 4--j = 2--dp[i] + 1 = dp[1] + 1 = 2--dp[j] = dp[2] = 1
更新:dp = [0, 1, 1, 3, 4]
i = 1--furthest = 4--j = 3--dp[i] + 1 = dp[1] + 1 = 2--dp[j] = dp[3] = 3
更新:dp = [0, 1, 1, 2, 4]
i = 1--furthest = 4--j = 4--dp[i] + 1 = dp[1] + 1 = 2--dp[j] = dp[4] = 4
更新:dp = [0, 1, 1, 2, 2]
i = 2--furthest = 3--j = 2--dp[i] + 1 = dp[2] + 1 = 2--dp[j] = dp[2] = 1
更新:dp = [0, 1, 1, 2, 2]
i = 2--furthest = 3--j = 3--dp[i] + 1 = dp[2] + 1 = 2--dp[j] = dp[3] = 2
更新:dp = [0, 1, 1, 2, 2]
i = 3--furthest = 4--j = 3--dp[i] + 1 = dp[3] + 1 = 3--dp[j] = dp[3] = 2
更新:dp = [0, 1, 1, 2, 2]
i = 3--furthest = 4--j = 4--dp[i] + 1 = dp[3] + 1 = 3--dp[j] = dp[4] = 2
更新:dp = [0, 1, 1, 2, 2]
i = 4--furthest = 8--j = 4--dp[i] + 1 = dp[4] + 1 = 3--dp[j] = dp[4] = 2
更新:dp = [0, 1, 1, 2, 2]
result = 2
Process finished with exit code 0
48. 旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
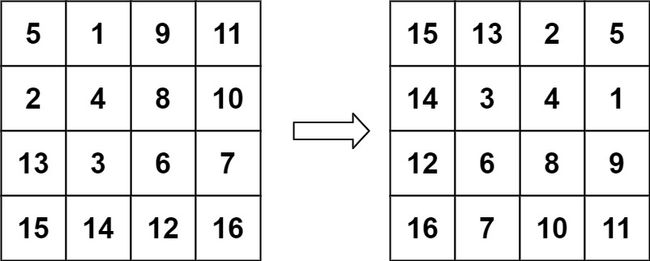
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
- n == matrix.length == matrix[i].length
- 1 <= n <= 20
- -1000 <= matrix[i][j] <= 1000
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
for(int i = 0; i < n / 2; i++){
for(int j = 0; j < (n + 1) / 2; j++){
int temp = matrix[i][j];
matrix[i][j] = matrix[n - j - 1][i];
matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
matrix[j][n - i - 1] = temp;
}
}
}
};
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
n = len(matrix)
for i in range(n // 2):
for j in range((n + 1) // 2):
temp = matrix[i][j]
matrix[i][j] = matrix[n - j - 1][i]
matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1]
matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1]
matrix[j][n - i - 1] = temp
15. 三数之和 【中等】
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
示例 2:
输入:nums = []
输出:[]
示例 3:
输入:nums = [0]
输出:[]
提示:
- 0 <= nums.length <= 3000
- − 1 0 5 < = n u m s [ i ] < = 1 0 5 -10^5 <= nums[i] <= 10^5 −105<=nums[i]<=105
方法一:排序 + 双指针
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
nums.sort()
ans = list()
# 枚举 a
for first in range(n):
# 需要和上一次枚举的数不相同
if first > 0 and nums[first] == nums[first - 1]:
continue
# c 对应的指针初始指向数组的最右端
third = n - 1
target = -nums[first]
# 枚举 b
for second in range(first + 1, n):
# 需要和上一次枚举的数不相同
if second > first + 1 and nums[second] == nums[second - 1]:
continue
# 需要保证 b 的指针在 c 的指针的左侧
while second < third and nums[second] + nums[third] > target:
third -= 1
# 如果指针重合,随着 b 后续的增加
# 就不会有满足 a+b+c=0 并且 b
if second == third:
break
if nums[second] + nums[third] == target:
ans.append([nums[first], nums[second], nums[third]])
return ans
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
n=len(nums)
res=[]
if(not nums or n<3):
return []
nums.sort()
res=[]
for i in range(n):
if(nums[i]>0):
return res
if(i>0 and nums[i]==nums[i-1]):
continue
L=i+1
R=n-1
while(L<R):
if(nums[i]+nums[L]+nums[R]==0):
res.append([nums[i],nums[L],nums[R]])
while(L<R and nums[L]==nums[L+1]):
L=L+1
while(L<R and nums[R]==nums[R-1]):
R=R-1
L=L+1
R=R-1
elif(nums[i]+nums[L]+nums[R]>0):
R=R-1
else:
L=L+1
return res
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort()
result = []
for i in range(len(nums) - 2):
if i > 0 and nums[i] == nums[i - 1]:
continue
left = i + 1
right = len(nums) - 1
while left < right:
sum3 = nums[i] + nums[left] + nums[right]
if sum3 == 0:
result.append([nums[i], nums[left], nums[right]])
while left < right and nums[left] == nums[left + 1]:
left += 1
while left < right and nums[right] == nums[right - 1]:
right -= 1
left += 1
right -= 1
elif sum3 < 0:
left += 1
else:
right -= 1
return result
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
sort(nums.begin(), nums.end()); // sort 的用法 默认最小排序
vector<vector<int>> result;
if(nums[0] > 0){
return result;
}
for(int i = 0; i < nums.size() - 2; i++) {
if(i > 0 && nums[i - 1] == nums[i])
continue;
int left = i + 1;
int right = nums.size() - 1;
while(left < right) {
int sum3 = nums[i] + nums[left] + nums[right];
if(sum3 == 0){
result.push_back({nums[i], nums[left], nums[right]});
while(left < right && nums[left + 1] == nums[left]) {
left++;
}
while(left < right && nums[right - 1] == nums[right]) {
right--;
}
left++;
right--;
}else if(sum3 < 0 ) {
left++;
} else {
right--;
}
}
}
return result;
}
};
53. 最大子数组和 【简单】
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [0]
输出:0
示例 4:
输入:nums = [-1]
输出:-1
示例 5:
输入:nums = [-100000]
输出:-100000
提示:
- 1 <= nums.length <= 3 * 104
- -105 <= nums[i] <= 105
进阶:如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。
https://leetcode-cn.com/problems/maximum-subarray/solution/dong-tai-gui-hua-fen-zhi-fa-python-dai-ma-java-dai/
方法一:动态规划【O(logn)】
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
size = len(nums)
if size == 0:
return 0
dp = [0 for _ in range(size)]
dp[0] = nums[0]
for i in range(1, size):
if dp[i - 1] >= 0:
dp[i] = dp[i - 1] + nums[i]
else:
dp[i] = nums[i]
return max(dp)
class Solution {
public:
int maxSubArray(vector<int> &nums) {
int numsSize = int(nums.size());
// 构建dp数组【dp[i]表示nums中以nums[i]结尾的最大子序和】
vector<int> dp(numsSize);
// 初始化dp数组边界
dp[0] = nums[0];
// 构建状态转移方程
for (int i = 1; i < numsSize; i++) {
if(dp[i - 1] > 0){
dp[i] = dp[i - 1] + nums[i];
}else{
dp[i] = nums[i];
}
}
return *max_element(dp.begin(), dp.end()); // 获取dp动态数组中的最大值
}
};
方法二:动态规划【O(logn)】
from typing import List
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
size = len(nums)
if size == 0:
return 0
dp = [0 for _ in range(size)]
dp[0] = nums[0]
for i in range(1, size):
dp[i] = max(dp[i - 1] + nums[i], nums[i])
return max(dp)
class Solution {
public:
int maxSubArray(vector<int> &nums) {
int numsSize = int(nums.size());
// 构建dp数组【dp[i]表示nums中以nums[i]结尾的最大子序和】
vector<int> dp(numsSize);
// 初始化dp数组边界
dp[0] = nums[0];
// 构建状态转移方程
for (int i = 1; i < numsSize; i++) {
dp[i] = max(dp[i - 1] + nums[i], nums[i]);
}
return *max_element(dp.begin(), dp.end()); // 获取dp动态数组中的最大值
}
};
方法三:分治法【【O(nlogn)】】
https://leetcode-cn.com/problems/maximum-subarray/solution/bao-li-qiu-jie-by-pandawakaka/
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
#递归终止条件
if n == 1:
return nums[0]
else:
#递归计算左半边最大子序和
max_left = self.maxSubArray(nums[0:len(nums) // 2])
#递归计算右半边最大子序和
max_right = self.maxSubArray(nums[len(nums) // 2:len(nums)])
#计算中间的最大子序和,从右到左计算左边的最大子序和,从左到右计算右边的最大子序和,再相加
max_l = nums[len(nums) // 2 - 1]
tmp = 0
for i in range(len(nums) // 2 - 1, -1, -1):
tmp += nums[i]
max_l = max(tmp, max_l)
max_r = nums[len(nums) // 2]
tmp = 0
for i in range(len(nums) // 2, len(nums)):
tmp += nums[i]
max_r = max(tmp, max_r)
#返回三个中的最大值
return max(max_right,max_left,max_l+max_r)
88. 合并两个有序数组 【简单】
给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中,使 nums1 成为一个有序数组。
初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。你可以假设 nums1 的空间大小等于 m + n,这样它就有足够的空间保存来自 nums2 的元素。
示例 1:
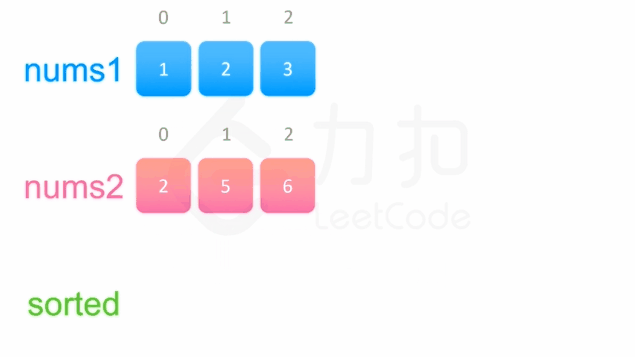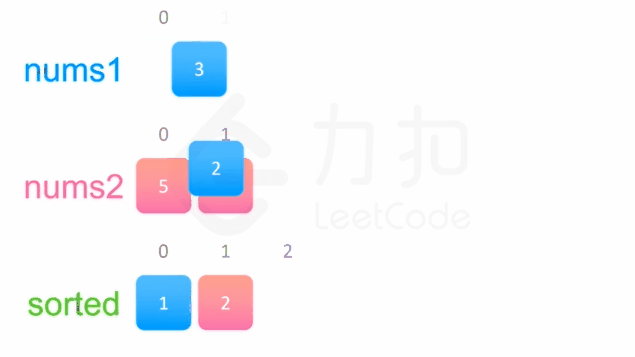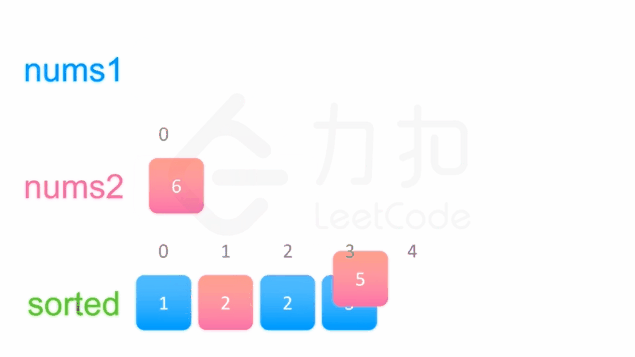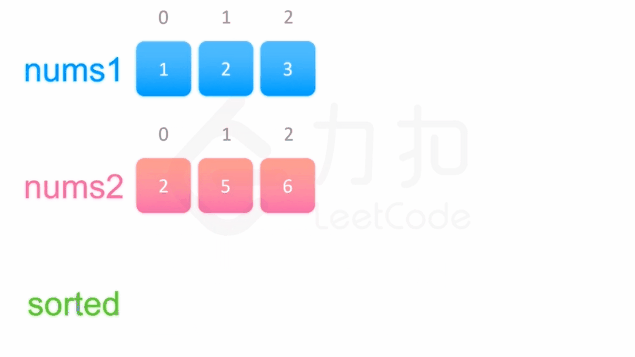
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
提示:
- nums1.length == m + n
- nums2.length == n
- 0 <= m, n <= 200
- 1 <= m + n <= 200
- − 1 0 9 < = n u m s 1 [ i ] , n u m s 2 [ i ] < = 1 0 9 -10^9 <= nums1[i], nums2[i] <= 10^9 −109<=nums1[i],nums2[i]<=109
方法一:直接合并后排序【 O ( ( m + n ) l o g ( m + n ) ) O((m+n)log(m+n)) O((m+n)log(m+n))】
最直观的方法是先将数组 nums 2 放进数组 nums 1 的尾部,然后直接对整个数组进行排序。
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
nums1[m:] = nums2
nums1.sort()
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
sorted = []
i = 0
j = 0
while i < m and j < n:
if nums1[i] < nums2[j]:
sorted.append(nums1[i])
i = i + 1
else:
sorted.append(nums2[j])
j = j + 1
while i < m:
sorted.append(nums1[i])
i = i +1
while j < n:
sorted.append(nums2[j])
j = j + 1
nums1[:] = sorted
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int sorted[m+n];
int i = 0;
int j = 0;
int k = 0;
while(i < m && j < n){
if(nums1[i] < nums2[j]){
sorted[k++] = nums1[i++];
}else{
sorted[k++] = nums2[j++];
}
}
while(i < m){
sorted[k++] = nums1[i++];
}
while(j < n){
sorted[k++] = nums2[j++];
}
for(int k = 0; k < m + n; k++){
nums1[k] = sorted[k];
}
}
};
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
vector<int> sorted;
int i = 0;
int j = 0;
while(i < m && j < n){
if(nums1[i] < nums2[j]){
sorted.push_back(nums1[i++]);
}else{
sorted.push_back(nums2[j++]);
}
}
while(i < m){
sorted.push_back(nums1[i++]);
}
while(j < n){
sorted.push_back(nums2[j++]);
}
for(int k = 0; k < m + n; k++){
nums1[k] = sorted[k];
}
}
};
方法三:双指针
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
sorted = []
p1, p2 = 0, 0
while p1 < m or p2 < n:
if p1 == m:
sorted.append(nums2[p2])
p2 += 1
elif p2 == n:
sorted.append(nums1[p1])
p1 += 1
elif nums1[p1] < nums2[p2]:
sorted.append(nums1[p1])
p1 += 1
else:
sorted.append(nums2[p2])
p2 += 1
nums1[:] = sorted
54-螺旋矩阵【剑指 Offer 29. 顺时针打印矩阵】
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
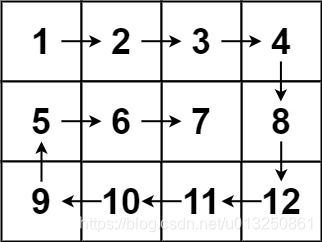
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
提示:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 10
- -100 <= matrix[i][j] <= 100
方法一:分别定位top bottom left right 四个点,即可完成动态获取
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
int left = 0, right = matrix[0].size();
int top = 0, bottom = matrix.size();
vector<int> result;
while(left < right && top < bottom){
for(int i = left; i < right; i++){
result.push_back(matrix[top][i]);
}
top++;
for(int i = top; i < bottom; i++){
result.push_back(matrix[i][right - 1]);
}
right--;
if(left < right && top < bottom){
for(int i = right - 1; i > left - 1; i--){
result.push_back(matrix[bottom - 1][i]);
}
bottom--;
for(int i = bottom - 1; i > top - 1; i--){
result.push_back(matrix[i][left]);
}
left++;
}
}
return result;
}
};
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
left = top = 0
right = len(matrix[0])
bottom = len(matrix)
ret = []
while left < right and top < bottom:
for i in range(left, right):
ret.append(matrix[top][i])
top += 1
for i in range(top, bottom):
ret.append(matrix[i][right - 1])
right -= 1
if left < right and top < bottom:
for i in range(right - 1, left - 1, -1):
ret.append(matrix[bottom - 1][i])
bottom -= 1
for i in range(bottom - 1, top - 1, -1):
ret.append(matrix[i][left])
left += 1
return ret
方法二:
https://leetcode-cn.com/problems/spiral-matrix/solution/ju-zhen-bian-li-wen-ti-de-si-bu-qu-by-fu-91za/
class Solution(object):
def spiralOrder(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: List[int]
"""
if not matrix or not matrix[0]: return []
M, N = len(matrix), len(matrix[0])
left, right, up, down = 0, N - 1, 0, M - 1
res = []
x, y = 0, 0
dirs = [(0, 1), (1, 0), (0, -1), (-1, 0)]
cur_d = 0
while len(res) != M * N:
res.append(matrix[x][y])
if cur_d == 0 and y == right:
cur_d += 1
up += 1
elif cur_d == 1 and x == down:
cur_d += 1
right -= 1
elif cur_d == 2 and y == left:
cur_d += 1
down -= 1
elif cur_d == 3 and x == up:
cur_d += 1
left += 1
cur_d %= 4
x += dirs[cur_d][0]
y += dirs[cur_d][1]
return res
剑指OfferII074-合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
- 1 < = i n t e r v a l s . l e n g t h < = 1 0 4 1 <= intervals.length <= 10^4 1<=intervals.length<=104
- intervals[i].length == 2
- 0 < = s t a r t i < = e n d i < = 1 0 4 0 <= starti <= endi <= 10^4 0<=starti<=endi<=104
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
intervals.sort(key=lambda x:x[0])
result = []
for interval in intervals:
# 如果列表为空
if not result:
result.append(interval)
else:
# 当前区间与上一区间不重合,直接添加
if interval[0] > result[-1][-1]:
result.append(interval)
else:
# 如果当前区间的右值大于result最后一个元素的右值
if interval[-1] > result[-1][-1]:
result[-1][-1] = interval[-1]
return result
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
sort(intervals.begin(), intervals.end());
vector<vector<int>> result;
for(vector<int> interval : intervals){
// 如果列表为空
if(result.size() == 0){
result.push_back(interval);
}else{
// 当前区间与上一区间不重合,直接添加
if(interval[0] > result.back()[1]){
result.push_back(interval);
}else{
// 如果当前区间的右值大于result最后一个元素的右值
if(interval[1] > result.back()[1]){
result.back()[1] = interval[1];
}
}
}
}
return result;
}
};
31. 下一个排列 【中等】
实现获取 下一个排列 的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
示例 4:
输入:nums = [1]
输出:[1]
提示:
- 1 <= nums.length <= 100
- 0 <= nums[i] <= 100
118. 杨辉三角 【简单】
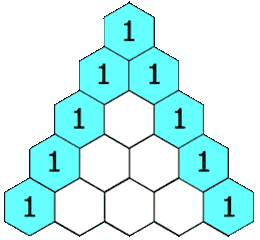
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
方法一:数学【 O ( O( O(\textit{numRows}^2)$】
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
ret = list()
for i in range(numRows):
row = list()
for j in range(0, i + 1):
if j == 0 or j == i:
row.append(1)
else:
row.append(ret[i - 1][j] + ret[i - 1][j - 1])
ret.append(row)
return ret
16. 最接近的三数之和 【中等】
给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
示例:
输入:nums = [-1,2,1,-4], target = 1
输出:2
解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
提示:
- 3 < = n u m s . l e n g t h < = 1 0 3 3 <= nums.length <= 10^3 3<=nums.length<=103
- − 1 0 3 < = n u m s [ i ] < = 1 0 3 -10^3 <= nums[i] <= 10^3 −103<=nums[i]<=103
- − 1 0 4 < = t a r g e t < = 1 0 4 -10^4 <= target <= 10^4 −104<=target<=104
class Solution:
def threeSumClosest(self, nums, target):
ret = float('inf')
nums.sort()
length = len(nums)
for i in range(length - 2):
left = i + 1
right = length - 1
while left < right:
tmp = nums[i] + nums[left] + nums[right]
ret = tmp if abs(tmp - target) < abs(ret - target) else ret
if tmp == target:
return target
if tmp > target:
right -= 1
else:
left += 1
return ret
55. 跳跃游戏 【中等】
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
- 1 < = n u m s . l e n g t h < = 3 ∗ 1 0 4 1 <= nums.length <= 3 * 10^4 1<=nums.length<=3∗104
- 0 < = n u m s [ i ] < = 1 0 5 0 <= nums[i] <= 10^5 0<=nums[i]<=105
方法一:贪心【O(n),其中 n 为数组的大小】
class Solution:
def canJump(self, nums: List[int]) -> bool:
n, rightmost = len(nums), 0
for i in range(n):
if i <= rightmost:
rightmost = max(rightmost, i + nums[i])
if rightmost >= n - 1:
return True
return False
283. 移动零 【简单】
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
说明:
- 必须在原数组上操作,不能拷贝额外的数组。
- 尽量减少操作次数。
方法一:双指针【O(n)】
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
n = len(nums)
left = right = 0
while right < n:
if nums[right] != 0:
nums[left], nums[right] = nums[right], nums[left]
left += 1
right += 1
59. 螺旋矩阵 II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
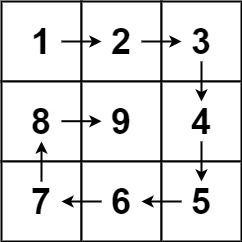
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
提示:
- 1 <= n <= 20
方法一:按层模拟
可以将矩阵看成若干层,首先填入矩阵最外层的元素,其次填入矩阵次外层的元素,直到填入矩阵最内层的元素。
定义矩阵的第 kk 层是到最近边界距离为 kk 的所有顶点。例如,下图矩阵最外层元素都是第 11 层,次外层元素都是第 22 层,最内层元素都是第 33 层。
[[1, 1, 1, 1, 1, 1],
[1, 2, 2, 2, 2, 1],
[1, 2, 3, 3, 2, 1],
[1, 2, 3, 3, 2, 1],
[1, 2, 2, 2, 2, 1],
[1, 1, 1, 1, 1, 1]]
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> matrix(n, vector<int>(n, -1));
int num = 1;
int top = 0;
int left = 0;
int right = n - 1;
int bottom = n - 1;
while(left <= right && top <= bottom){
for(int col = left; col < right + 1; col++){
matrix[top][col] = num;
num++;
}
for(int row = top + 1; row < bottom + 1; row++){
matrix[row][right] = num;
num++;
}
if(left < right && top < bottom){
for(int col = right - 1; col > left - 1; col--){
matrix[bottom][col] = num;
num++;
}
for(int row = bottom - 1; row > top; row--){
matrix[row][left] = num;
num++;
}
}
top++;
left++;
right--;
bottom--;
}
return matrix;
}
};
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
matrix = [[-1]*n for _ in range(n)]
num = 1
top = 0
left = 0
right = n - 1
bottom = n - 1
while left <= right and top <= bottom:
for col in range(left,right +1):
matrix[top][col] = num
num +=1
for row in range(top + 1, bottom +1):
matrix[row][right] = num
num+=1
if left < right and top < bottom:
for col in range(right - 1, left - 1, -1):
matrix[bottom][col] = num
num +=1
for row in range(bottom - 1,top,-1):
matrix[row][left] = num
num+=1
top +=1
left +=1
right -=1
bottom -=1
return matrix
118. 杨辉三角
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1
输出: [[1]]
提示:
- 1 <= numRows <= 30
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
triangel = [[1 for _ in range(i + 1)] for i in range(numRows)]
if numRows <= 2:
return triangel
for i in range(2, numRows):
for j in range(1, len(triangel[i]) - 1):
triangel[i][j] = triangel[i - 1][j - 1] + triangel[i - 1][j]
return triangel
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> triangel(numRows, vector<int>(numRows, 1)); // 二维数组,初始化行数为numRows,列数为numRows,元素值都为1
for (int i = 0; i < numRows; i++) {
triangel[i].resize(i + 1); // 调整当前行的列数
for (int j = 1; j < i; j++) {
triangel[i][j] = triangel[i - 1][j] + triangel[i - 1][j - 1];
}
}
return triangel;
}
};
867. 转置矩阵
给你一个二维整数数组 matrix, 返回 matrix 的 转置矩阵 。
矩阵的 转置 是指将矩阵的主对角线翻转,交换矩阵的行索引与列索引。
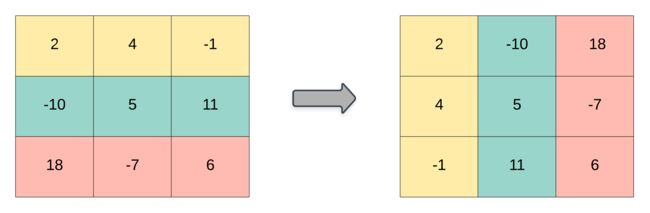
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[1,4,7],[2,5,8],[3,6,9]]
示例 2:
输入:matrix = [[1,2,3],[4,5,6]]
输出:[[1,4],[2,5],[3,6]]
提示:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 1000
- 1 <= m * n <= 1 0 5 10^5 105
- − 1 0 9 < = m a t r i x [ i ] [ j ] < = 1 0 9 -10^9 <= matrix[i][j] <= 10^9 −109<=matrix[i][j]<=109
class Solution:
def transpose(self, matrix: List[List[int]]) -> List[List[int]]:
m = len(matrix)
n = len(matrix[0])
result = [[0] * m for _ in range(n)]
for i in range(m):
for j in range(n):
result[j][i] = matrix[i][j]
return result
class Solution {
public:
vector<vector<int>> transpose(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
vector<vector<int>> result(n, vector<int>(m));
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
result[j][i] = matrix[i][j];
}
}
return result;
}
};
面试题 01.08. 零矩阵
编写一种算法,若M × N矩阵中某个元素为0,则将其所在的行与列清零。
示例 1:
输入:
[
[1,1,1],
[1,0,1],
[1,1,1]
]
输出:
[
[1,0,1],
[0,0,0],
[1,0,1]
]
示例 2:
输入:
[
[0,1,2,0],
[3,4,5,2],
[1,3,1,5]
]
输出:
[
[0,0,0,0],
[0,4,5,0],
[0,3,1,0]
]
class Solution {
public:
void setZeroes(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
vector<bool> row(m, false);
vector<bool> col(n, false);
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(matrix[i][j] == 0){
row[i] = true;
col[j] = true;
}
}
}
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(row[i] == true || col[j] == true){
matrix[i][j] = 0;
}
}
}
}
};
class Solution:
def setZeroes(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
m = len(matrix)
n = len(matrix[0])
row = [False] * m
col = [False] * n
for i in range(m):
for j in range(n):
if matrix[i][j] == 0:
row[i], col[j] = True, True
print(row, col)
for i in range(m):
for j in range(n):
if row[i] == True or col[j] == True:
matrix[i][j] = 0
189. 轮转数组
给你一个数组,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
提示:
- 1 <= nums.length <= 105 105 105
- − 2 31 < = n u m s [ i ] < = 2 31 − 1 -2^{31} <= nums[i] <= 2^{31} - 1 −231<=nums[i]<=231−1
- 0 < = k < = 1 0 5 0 <= k <= 10^5 0<=k<=105
进阶:
尽可能想出更多的解决方案,至少有 三种 不同的方法可以解决这个问题。
你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗?
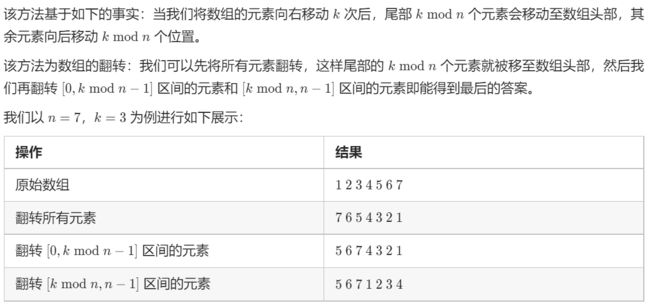
class Solution {
public:
void rotate(vector<int>& nums, int k) {
k = k % nums.size();
reverse(nums, 0, nums.size() - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.size() - 1);
}
void reverse(vector<int>& nums, int left, int right){
while(left <= right){
swap(nums[left], nums[right]);
left++;
right--;
}
}
};
class Solution:
def rotate(self, nums: List[int], k: int) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
k = k % len(nums)
self.reverse(nums, 0, len(nums) - 1)
self.reverse(nums, 0, k - 1)
self.reverse(nums, k, len(nums) - 1)
def reverse(self, nums, left, right):
while left <= right:
nums[left], nums[right] = nums[right], nums[left]
left += 1
right -= 1
238. 除自身以外数组的乘积【剑指 Offer 66. 构建乘积数组】
给定一个数组 A[0,1,…,n-1],请构建一个数组 B[0,1,…,n-1],其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。
示例:
输入: [1,2,3,4,5]
输出: [120,60,40,30,24]
提示:
- 所有元素乘积之和不会溢出 32 位整数
- a.length <= 100000
class Solution {
public:
vector<int> constructArr(vector<int>& a) {
vector<int> left(a.size(), 1);
vector<int> right(a.size(), 1);
vector<int> result(a.size(), 1);
for(int i = 1; i < a.size(); i++){
left[i] = left[i - 1] * a[i - 1];
}
for(int i = a.size() - 2; i > -1; i--){
right[i] = right[i + 1] * a[i + 1];
}
for(int i = 0; i < a.size(); i++){
result[i] = left[i] * right[i];
}
return result;
}
};
class Solution:
def constructArr(self, a: List[int]) -> List[int]:
left = [1] * len(a)
right = [1] * len(a)
result = [1] * len(a)
for i in range(1, len(a)):
left[i] = left[i - 1] * a[i - 1]
for i in range(len(a) - 2, -1, -1):
right[i] = right[i + 1] * a[i + 1]
for i in range(len(a)):
result[i] = left[i] * right[i]
return result
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
n = len(nums)
result = [1 for _ in range(n)] # 结果存储数组
left = 1 # 临时保存右侧积
for i in range(1, n): # 计算左侧积
left *= nums[i - 1]
result[i] = left
right = 1 # 临时保存右侧积
for j in range(n - 2, -1, -1): # 计算右侧积
right *= nums[j + 1]
result[j] *= right
return result