第13章 二叉树模型及其扩展

这学期会时不时更新一下伊曼纽尔·德曼（Emanuel Derman） 教授与迈克尔B.米勒（Michael B. Miller）的《The Volatility Smile》这本书，本意是协助导师课程需要，发在这里有意的朋友们可以学习一下，思路不一定够清晰且由于分工原因我是从书本第13章写起，还请大家见谅。

第13章 二叉树模型及其扩展

股价变动方式的二叉树模型

假设股息率=0，在BSM模型下的股价满足：
$$d(\ln (S))=\mu dt+\sigma dZ$$
单位时间内，股票预期对数回报=$\mu$，对数回报波动率=$\sigma$，$t$ 时刻后的总方差=${\sigma }^{2}t$

根据伊藤引理推导（令$\ln (S)=P$）：
$$\begin{gathered} d(S)=d(e^P)=(\frac{\partial e^P}{\partial P}\mu +\frac{\partial e^P}{\partial t}+\frac{1}{2}\frac{{\partial }^2{e}^P}{\partial P^2}{\sigma }^2)dt+\frac{\partial e^P}{\partial P}\sigma dZ \\ =(e^P\mu +\frac{1}{2}{e}^P{\sigma }^2)dt+e^P\sigma dZ \\ =(\mu +\frac{1}{2}{\sigma }^2)Sdt+\sigma SdZ \end{gathered}$$
上式表明：股票价格的预期回报=$\mu +\frac{1}{2}{\sigma }^2$

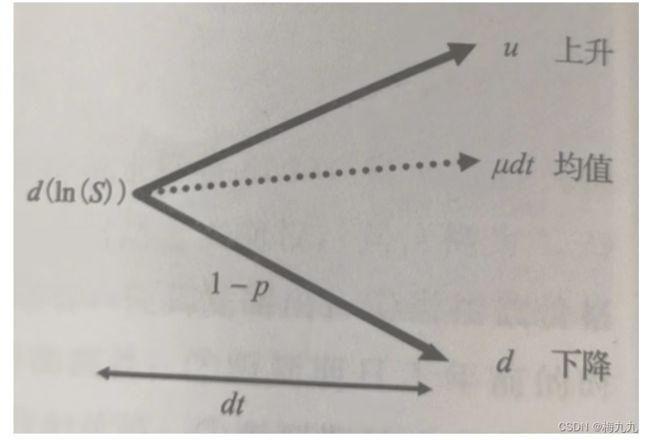
上图展示了单期二叉树下，$dt$ 时间间隔内股价的变动情况。$p,u,d$ 都是由 $\mu ,\sigma$ 决定的。假设上述描述的是真实的股价变动，则 $p，1-p$ 都为真实的概率。真实事件发生的概率通常被称为 $p$ 测度。

对数回报=$u$ 的概率为 $p$，对数回报=$d$ 的概率为 $(1-p)$，均值=$\mu dt$。考虑均值和方程，可以进行如下推导：
$$\begin{gathered} pu+(1-p)d=\mu dt \\ p(u-\mu dt{)}^2+(1-p)(d-\mu dt{)}^2={\sigma }^{2}dt \end{gathered}$$
将第一个式子中的 $\mu dt$ 带入第二个式子可得：
$$\begin{gathered} p[u-pu-(1-p)d{]}^2+(1-p)[d-pu-(1-p)d{]}^2={\sigma }^{2}dt \\ p[(u-d)(1-p){]}^2+(1-p)[p(d-u){]}^2={\sigma }^{2}dt \\ p(u-d{)}^2[(1-p{)}^2+(1-p)p]={\sigma }^{2}dt \\ p(1-p)(u-d{)}^2={\sigma }^{2}dt \end{gathered}$$
对于 $p,u,d$，上述式子只给出了两个约束条件，而这个方程有一系列解。因此，可以自己选择引入额外的约束条件，使其更为简便。

1、Cox-Ross-Rubinstein模型

令 $u+d=0$，保证二叉树中心位置保持不变，即可以得到Cox-Ross-Rubinstein（CRR）模型，上述两个约束条件可以改写为：
$$\begin{gathered} (2p-1)u=\mu dt \\ 4p(1-p)u^2={\sigma }^{2}dt \end{gathered}$$
将1式取平方与2式相加可得：
$$\begin{gathered} (4p^2-4p+1+4p-4p^2)u^2={\mu }^{2}d{t}^2+{\sigma }^{2}dt \\ {u}^2={\mu }^{2}d{t}^2+{\sigma }^{2}dt \end{gathered}$$
当 $dt\to 0$ 时，$d{t}^2$ 相对于 $dt$ 可以忽略不计：
$$\begin{gathered} dt\to 0:u^2={\sigma }^{2}dt \\ u=\sigma \sqrt{dt},d=-\sigma \sqrt{dt} \end{gathered}$$
$u,d$ 即为上述表达式，带入1式可得：
$$\begin{gathered} (2p-1)\sigma \sqrt{dt}=\mu dt \\ p=\frac{1}{2}+\frac{1}{2}\frac{\mu }{\sigma }\sqrt{dt} \end{gathered}$$
至此，在CRR模型下，我们用 $\mu ,\sigma$ 表示 $p,u,d$

二叉树过程的均值与方差如下：
$$\begin{gathered} pu+(1-p)d=(\frac{1}{2}+\frac{1}{2}\frac{\mu }{\sigma }\sqrt{dt})\sigma \sqrt{dt}+(1-\frac{1}{2}-\frac{1}{2}\frac{\mu }{\sigma }\sqrt{dt})(-\sigma \sqrt{dt})=\mu dt \\ p(1-p)(u-d{)}^2=(\frac{1}{2}+\frac{1}{2}\frac{\mu }{\sigma }\sqrt{dt})(\frac{1}{2}-\frac{1}{2}\frac{\mu }{\sigma }\sqrt{dt})(\sigma \sqrt{dt}+\sigma \sqrt{dt}{)}^2 \\ =(1-\frac{{\mu }^2}{{\sigma }^2}dt)({\sigma }^{2}dt)={\sigma }^{2}dt-{\mu }^{2}d{t}^2 \end{gathered}$$
当 $dt\to 0$ 时，$d{t}^2$ 相对于 $dt$ 可以忽略不计：
$$p(1-p)(u-d{)}^2={\sigma }^{2}dt$$
满足一般的约束条件。

不过，如果 $dt\ne 0$，计算得到的方差会比实际方差略小，收敛过程相比实际情况也会稍慢一些。

Jarrow-Rudd模型

该模型令 $p=\frac{1}{2}$，即股价上行下行概率相等：
$$\begin{gathered} \frac{1}{2}u+\frac{1}{2}d=\mu dt\to u+d=2\mu dt \\ \frac{1}{4}(u-d{)}^2={\sigma }^{2}dt\to u-d=2\sigma \sqrt{dt} \end{gathered}$$
易得：
$$\begin{gathered} u=\mu dt+\sigma \sqrt{dt} \\ d=\mu dt-\sigma \sqrt{dt} \end{gathered}$$
设初始股价=$S_0$，在一个时间段 $dt$ 后，预期股价如下推导：
$$E[S_{dt}]=\frac{1}{2}{S}_0{e}^u+\frac{1}{2}{S}_0{e}^d=\frac{1}{2}{S}_0{e}^{\mu dt}(e^{\sigma \sqrt{dt}}+e^{-\sigma \sqrt{dt}})$$
对括号中的两项进行泰勒二阶展开（将 $\sigma \sqrt{dt}$ 看作整体）：
$$E[S_{dt}]\approx \frac{1}{2}{S}_0{e}^{\mu dt}(1+\sigma \sqrt{dt}+\frac{{\sigma }^{2}dt}{2}+1-\sigma \sqrt{dt}+\frac{{\sigma }^{2}dt}{2})=S_0{e}^{\mu dt}(1+\frac{{\sigma }^{2}dt}{2})$$
已知对 $e^x$ 做一阶泰勒展开为：$e^x\approx 1+x$，将该近似带入上式得：
$$E[S_{dt}]\approx S_0{e}^{\mu dt}(1+\frac{{\sigma }^{2}dt}{2})\approx S_0{e}^{\mu dt}{e}^{\frac{{\sigma }^{2}dt}{2}}=S_0{e}^{(\mu +\frac{{\sigma }^2}{2})dt}$$
当 $dt\to 0$ 时，股票预期连续复利回报等于 $\mu +\frac{{\sigma }^2}{2}$，与伊藤引理相符

期权估值的二叉树模型

期权估值

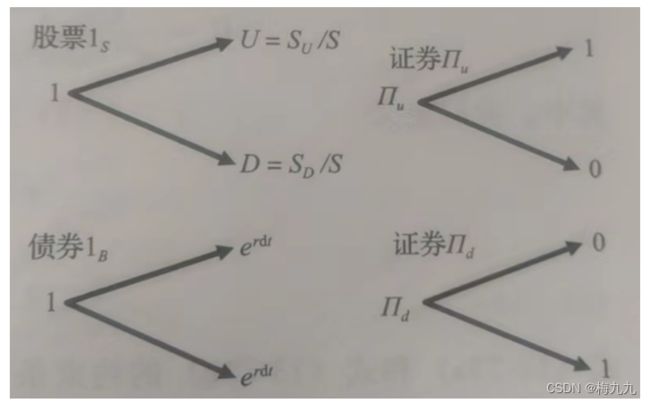
将一只股票 S 和一个无风险债券 B 分解为两个基础状态依赖证券，${\Pi }_u,{\Pi }_d$，其中，在一个微小时间间隔 $dt$ 之后，${\Pi }_u$ 表示当股价上行时支付1美元，股价下行时不支付；${\Pi }_d$ 表示当股价下行时支付1美元，股价上行时不支付。用 $1_S$ 表示买入价值为1美元的股票，用 $1_B$ 表示买入价值为1美元的无风险债券

用 $S_U,S_D$ 表示股价上行和下行状态，假设初始股价=$S$，股价上行时，$1_S$ 的价值等于 $U=S_U/S\equiv e^u$；股价下行时，价值等于 $D=S_D/S\equiv e^d$。而投资于无风险债券的 $1_B$ 在股价上行和下行时都=$e^{rdt},r$ 表示无风险利率。具体如下图所示：

可以将证券 ${\Pi }_u$ 表示成 $1_S,1_B$ 的线性关系式：${\Pi }_u=\alpha 1_S+\beta 1_B$，当股价上行下行的时候，令等式右侧的损益等于 ${\Pi }_u$ 的损益，即可求解得到 $\alpha ,\beta$

一个同时持有 ${\Pi }_u,{\Pi }_d$ 的组合在 $dt$ 时间段后价值一定=1美元，等同于一个在 $dt$ 时面值为1美元的无风险债券，即有如下式子：
$${\Pi }_u+{\Pi }_d=e^{-rdt}{1}_B$$
考虑 ${\Pi }_u$，在股价上行和下行的状态，分别有如下等式：
$$\begin{gathered} \alpha U+\beta e^{rdt}=1 \\ \alpha D+\beta e^{rdt}=0 \end{gathered}$$
联立可得：
$$\begin{gathered} \alpha =\frac{1}{U-D} \\ \beta =\frac{-e^{-rdt}D}{U-D} \end{gathered}$$
带入线性关系式可得：
$$\begin{gathered} {\Pi }_u=\frac{1}{U-D}{1}_S+\frac{-e^{-rdt}D}{U-D}{1}_B=\frac{e^{rdt}{1}_S-D{1}_B}{e^{rdt}(U-D)} \\ {\Pi }_d=e^{-rdt}{1}_B-\frac{e^{rdt}{1}_S-D{1}_B}{e^{rdt}(U-D)}=\frac{U{1}_B-e^{rdt}{1}_S}{e^{rdt}(U-D)} \end{gathered}$$
状态依赖证券的初始价值等于：
$$\begin{gathered} \Pi =\frac{e^{rdt}-D}{e^{rdt}(U-D)}\equiv e^{-rdt}q \\ \Pi =\frac{U-e^{rdt}}{e^{rdt}(U-D)}\equiv e^{-rdt}(1-q) \end{gathered}$$
其中，定义：
$$\begin{gathered} q=\frac{e^{rdt}-D}{U-D} \\ 1-q=\frac{U-e^{rdt}}{U-D} \end{gathered}$$
上述约束条件说明，在风险中性条件下，股价上行和下行不存在无风险套利机会

$q,1-q$ 不是“真实”概率，是伪概率。通常将这些伪概率称为 $q$ 测度，而相对应的真实概率则称为 $p$ 测度

为了更能反映本质，$q$ 的定义也可以写作：
$$\begin{gathered} qU+(1-q)D=e^{rdt} \\ qS{e}^u+(1-q)S{e}^d=S{e}^{rdt} \\ S=e^{-rdt}[q{S}_u+(1-q)S_d] \end{gathered}$$
因此，在 $q$ 测度中，股票的现值等于其未来价格按照概率加权之后，用无风险利率折现后的价值

将股票 S 换成任意的衍生证券 C，同理都有：
$$C=e^{-rdt}[q{C}_u+(1-q)C_d]$$

BSM偏微分方程与二叉树模型

当 $dt\to 0$ 时，对上式求导即可得到BSM的偏微分方程，利用之前得到的CRR公式：
$$u=\sigma \sqrt{dt},d=-\sigma \sqrt{dt}$$
推导得：
$$\begin{gathered} q=\frac{e^{rdt}-D}{U-D}=\frac{e^{rdt}-e^{-\sigma \sqrt{dt}}}{e^{\sigma \sqrt{dt}}-e^{-\sigma \sqrt{dt}}} \\ 1-q=\frac{U-e^{rdt}}{U-D}=\frac{e^{\sigma \sqrt{dt}}-e^{rdt}}{e^{\sigma \sqrt{dt}}-e^{-\sigma \sqrt{dt}}} \end{gathered}$$
带入上述与C相关的方程可得：
$$\begin{gathered} C=e^{-rdt}[q{C}_u+(1-q)C_d]=e^{-rdt}[\frac{e^{rdt}-e^{-\sigma \sqrt{dt}}}{e^{\sigma \sqrt{dt}}-e^{-\sigma \sqrt{dt}}}{C}_u+\frac{e^{\sigma \sqrt{dt}}-e^{rdt}}{e^{\sigma \sqrt{dt}}-e^{-\sigma \sqrt{dt}}}{C}_d] \\ {e}^{rdt}C=\frac{e^{rdt}-e^{-\sigma \sqrt{dt}}}{e^{\sigma \sqrt{dt}}-e^{-\sigma \sqrt{dt}}}{C}_u+\frac{e^{\sigma \sqrt{dt}}-e^{rdt}}{e^{\sigma \sqrt{dt}}-e^{-\sigma \sqrt{dt}}}{C}_d \end{gathered}$$
将 $C$ 表示成 $S,t$ 的连续函数，于是 $C=C(S,t)$，并且：
$$\begin{gathered} C_u=C(S{e}^{\sigma \sqrt{dt}},t+dt) \\ {C}_d=C(S{e}^{-\sigma \sqrt{dt}},t+dt) \end{gathered}$$
带入得：
$$\begin{gathered} C=e^{-rdt}[q{C}_u+(1-q)C_d]=e^{-rdt}[qC(S{e}^{\sigma \sqrt{dt}},t+dt)+(1-q)C(S{e}^{-\sigma \sqrt{dt}},t+dt)] \\ {e}^{rdt}C=qC(S{e}^{\sigma \sqrt{dt}},t+dt)+(1-q)C(S{e}^{-\sigma \sqrt{dt}},t+dt) \end{gathered}$$
通过泰勒展开可得：
$$\begin{gathered} (1+rdt)C=q[C+\frac{\partial C}{\partial S}S(\sigma \sqrt{dt}+\frac{1}{2}{\sigma }^{2}dt)+\frac{1}{2}\frac{{\partial }^{2}C}{\partial S^2}{S}^2{\sigma }^{2}dt+\frac{\partial C}{\partial t}dt] \\ +(1-q)[C+\frac{\partial C}{\partial S}S(-\sigma \sqrt{dt}+\frac{1}{2}{\sigma }^{2}dt)+\frac{1}{2}\frac{{\partial }^{2}C}{\partial S^2}{S}^2{\sigma }^{2}dt+\frac{\partial C}{\partial t}dt] \\ =C+\frac{\partial C}{\partial S}S[(2q-1)\sigma \sqrt{dt}+\frac{1}{2}{\sigma }^{2}dt]+\frac{1}{2}\frac{{\partial }^{2}C}{\partial S^2}{S}^2{\sigma }^{2}dt+\frac{\partial C}{\partial t}dt \end{gathered}$$
在该式中我们需要求得 $(2q-1)$，进行如下推导：
$$\begin{gathered} q=\frac{e^{rdt}-e^{-\sigma \sqrt{dt}}}{e^{\sigma \sqrt{dt}}-e^{-\sigma \sqrt{dt}}} \\ 1-q=\frac{e^{\sigma \sqrt{dt}}-e^{rdt}}{e^{\sigma \sqrt{dt}}-e^{-\sigma \sqrt{dt}}} \\ 2q-1=\frac{e^{rdt}-e^{-\sigma \sqrt{dt}}}{e^{\sigma \sqrt{dt}}-e^{-\sigma \sqrt{dt}}}-\frac{e^{\sigma \sqrt{dt}}-e^{rdt}}{e^{\sigma \sqrt{dt}}-e^{-\sigma \sqrt{dt}}} \\ =\frac{e^{rdt}-e^{-\sigma \sqrt{dt}}-(e^{\sigma \sqrt{dt}}-e^{rdt})}{e^{\sigma \sqrt{dt}}-e^{-\sigma \sqrt{dt}}} \\ =\frac{2e^{rdt}-e^{-\sigma \sqrt{dt}}-e^{\sigma \sqrt{dt}}}{e^{\sigma \sqrt{dt}}-e^{-\sigma \sqrt{dt}}} \end{gathered}$$
将领头阶 $dt$ 代入得：
$$\begin{gathered} 2q-1=\frac{2e^{rdt}-e^{-\sigma \sqrt{dt}}-e^{\sigma \sqrt{dt}}}{e^{\sigma \sqrt{dt}}-e^{-\sigma \sqrt{dt}}} \\ \approx \frac{2rdt+\sigma \sqrt{dt}-\frac{1}{2}{\sigma }^{2}dt-\sigma \sqrt{dt}-\frac{1}{2}{\sigma }^{2}dt}{\sigma \sqrt{dt}+\frac{1}{2}{\sigma }^{2}dt+\sigma \sqrt{dt}-\frac{1}{2}{\sigma }^{2}dt} \\ =\frac{2rdt-{\sigma }^{2}dt}{2\sigma \sqrt{dt}} \\ =\frac{(r-\frac{1}{2}{\sigma }^2)\sqrt{dt}}{\sigma } \end{gathered}$$
带入之前得泰勒展开式可得：
$$\begin{gathered} (1+rdt)C=C+\frac{\partial C}{\partial S}S[(2q-1)\sigma \sqrt{dt}+\frac{1}{2}{\sigma }^{2}dt]+\frac{1}{2}\frac{{\partial }^{2}C}{\partial S^2}{S}^2{\sigma }^{2}dt+\frac{\partial C}{\partial t}dt \\ =C+\frac{\partial C}{\partial S}S[\frac{(r-\frac{1}{2}{\sigma }^2)\sqrt{dt}}{\sigma }\sigma \sqrt{dt}+\frac{1}{2}{\sigma }^{2}dt]+\frac{1}{2}\frac{{\partial }^{2}C}{\partial S^2}{S}^2{\sigma }^{2}dt+\frac{\partial C}{\partial t}dt \\ =C+\frac{\partial C}{\partial S}S[(r-\frac{1}{2}{\sigma }^2)dt+\frac{1}{2}{\sigma }^{2}dt]+\frac{1}{2}\frac{{\partial }^{2}C}{\partial S^2}{S}^2{\sigma }^{2}dt+\frac{\partial C}{\partial t}dt \\ =C+\frac{\partial C}{\partial S}rSdt+\frac{1}{2}\frac{{\partial }^{2}C}{\partial S^2}{S}^2{\sigma }^{2}dt+\frac{\partial C}{\partial t}dt \end{gathered}$$
两边同除 $dt$，可得：
$$Cr=\frac{\partial C}{\partial S}rS+\frac{1}{2}\frac{{\partial }^{2}C}{\partial S^2}{S}^2{\sigma }^2+\frac{\partial C}{\partial t}$$
上式即为BSM偏微分方程。

BSM模型的扩展

基本案例：股息率和无风险利率都等于0，计价单位为无风险债券

在该种情况下，对于标准欧式看涨期权，BSM价格为：
$$\begin{gathered} C(S,K,v)=SN(d_1)-KN(d_2) \\ {d}_{1,2}=\frac{1}{v}\ln (\frac{S}{K})\pm \frac{v}{2} \end{gathered}$$
其中 $v=\sigma \sqrt{\tau }$，$\tau$ 表示到期时间

上式包含了两个证券，即股票和债券。下面我们用债券的价格给股票和看涨期权报价——即将债券价格看作货币或者计价单位

令 $C_B=C/B,S_B=S/B$，相当于用一单位无风险债券给证券报价。若无风险利率=0，则该无风险债券的现值及未来价值都等于面值，且 $B=K,B_B=1$。可以将上式改写为：
$$\begin{gathered} C_B(S_B,v)=S_{B}N(d_1)-N(d_2) \\ {d}_{1,2}=\frac{1}{v}\ln (S_B)\pm \frac{v}{2} \end{gathered}$$
$C_B,S_B$ 不再用美元、欧元或者任何其他一种货币来计价，而是以无风险债券作为计价单位

模型扩展：利率不等于0

此时债券按无风险利率增长，有 $dB=rBdt$，债券价格随时间变化而变化。若债券面值=$K$，距离到期日 $\tau$，则债券价格$B=K{e}^{-r\tau }$

同样的，以债券现值 $B$ 为计价单位，有：
$$B_B=1,S_B=S/B=e^{r\tau }S/K$$
已知：
$$\begin{gathered} C_B(S_B,v,r,\tau )=S_{B}N(d_1)-N(d_2) \\ {d}_{1,2}=\frac{1}{v}\ln (S_B)\pm \frac{v}{2} \end{gathered}$$
上述等式乘以债券当前价值：$B=K{e}^{-r\tau }$，可得：
$$\begin{gathered} C(S,K,\sigma ,r,\tau )=SN(d_1)-K{e}^{-r\tau }N(d_2) \\ {d}_{1,2}=\frac{1}{v}[\ln (\frac{S{e}^{r\tau }}{K})\pm \frac{v^2}{2}],v=\sigma \sqrt{\tau } \end{gathered}$$
上述式子即为标准的BSM公式

当无风险利率 $\ne$ 0时，股票的相对波动率就是以债券价格为计价单位的股价波动率。而如果利率是一个随机变量，那么 $B$ 也是一个随机变量

模型扩展：股票支付连续股利，且股息率已知

假设一只股票股息率为 $b$，按每一单位时间支付。相当于在银行储蓄1美元，而银行按照自己的计价货币支付连续利息 $r$，到到期日时，1美元会增长至 $e^{b\tau }$ 美元，而我们将股息再投资买人股票，那么最终会得到 $e^{b\tau }$ 份股票。1份股票为标的资产的欧式看涨期权在到期日的损益为 $\max [S_T-K，0]$，要想获得这一期权，你可以在今天买入以 $e^{-b\tau }$ 份股票为标的资产的期权，这些股票初始价值为 $S{e}^{-b\tau }$，但是由于进行了再投资，在到期之日这些股票的价值就等于 $S_T$。因此，你可以将式：
$$\begin{gathered} C(S,K,\sigma ,r,\tau )=SN(d_1)-K{e}^{-r\tau }N(d_2) \\ {d}_{1,2}=\frac{1}{v}[\ln (\frac{S{e}^{r\tau }}{K})\pm \frac{v^2}{2}],v=\sigma \sqrt{\tau } \end{gathered}$$
中的 $S$ 替换成为 $S{e}^{-b\tau }$：
$$\begin{gathered} C(S,K,\sigma ,r,\tau )=S{e}^{-b\tau }N(d_1)-K{e}^{-r\tau }N(d_2) \\ {d}_{1,2}=\frac{1}{v}[\ln (\frac{S{e}^{(r-b)\tau }}{K})\pm \frac{v^2}{2}],v=\sigma \sqrt{\tau } \end{gathered}$$
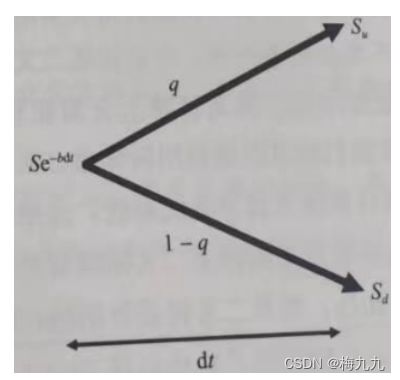
二叉树：若股息率= $b$，那么 $e^{-b(dt)}$ 份价格为 $S$ 的股票在 $dt$ 时间后会增长成1份股票，价格等于 $S_u$ 或 $S_d$，如图所示：

假设无风险利率为 $r$，根据定义，$q$ 测度需要考虑股票的总回报，既包括股利支付，也包括到期日的股票价值。对 $dt$ 时间段后预期股价的约束条件为：
$$q{S}_u+(1-q)S_d=e^{rdt}(S{e}^{-bdt})=S{e}^{(r-b)dt}\equiv F$$
其中 $F$ 表示前瞻股价，其中包括了支付的股利

风险中性下的 $q$ 测度就可以表示为：
$$q=\frac{F-S_d}{S_u-S_d}$$
期权不支付股利，因此它们的预期损益仍然按照无风险利率进行折现：
$$q{C}_u+(1-q)C_d=C{e}^{rdt}$$

时间依赖下的波动率：波动率微笑有期限结构但没有斜度

改变波动率的假设。现在，假设未来股票的回报波动率时一个与时间 $t$ 相关的函数，则股价变动就可以描述为：
$$\frac{dS}{S}=\mu dt+\sigma (t)dZ$$
假设建立CRR二叉树模型，阶段1波动率=${\sigma }_1$，阶段2波动率=${\sigma }_2$，如果每个阶段的时间间隔 $dt$ 是相等的，除非 ${\sigma }_1={\sigma }_2$，即 $\sigma (t)$ 保持不变，否则这个二叉树模型将不是“封闭”的

要使得二叉树模型封闭，只需改变不同节点之间的时间间隔：
$$\begin{gathered} S{e}^{{\sigma }_1\sqrt{d{t}_1}-{\sigma }_2\sqrt{d{t}_2}}=S{e}^{-{\sigma }_1\sqrt{d{t}_1}+{\sigma }_2\sqrt{d{t}_2}} \\ \to {\sigma }_1\sqrt{d{t}_1}={\sigma }_2\sqrt{d{t}_2} \end{gathered}$$
我们需要的是不同阶段的总波动率相等，即 ${\sigma }_i\sqrt{d{t}_i}$ 保持不变

总的来说，对于确定到期期限 $T$ 和已知波动率序列 ${\sigma }_i$​，有：
$$\begin{gathered} {\sigma }_1\sqrt{d{t}_1}={\sigma }_i\sqrt{d{t}_i} \\ \to \frac{d{t}_i}{d{t}_1}=\frac{{\sigma }_1^2}{{\sigma }_i^2} \end{gathered}$$
所以可以得到：
$$T=\sum _{i=1}^{N}d{t}_i=d{t}_1\sum _{i=1}^N\frac{d{t}_i}{d{t}_1}=d{t}_1\sum _{i=1}^N\frac{{\sigma }_1^2}{{\sigma }_i^2}$$
覆盖至到期日需要多少个时间间隔，可以通过解上述方程求得 $N$。

关于时间依赖波动率，还有一点需要注意：每一时间阶段内的二项无套利概率 $q$ 并不需要保持不变，可以随着时间的变化而变化，将 $dt$ 用 $d{t}_i$ 代替可得：
$$\begin{gathered} q_i=\frac{e^{rd{t}_i}-e^{-{\sigma }_i\sqrt{d{t}_i}}}{e^{{\sigma }_i\sqrt{d{t}_i}}-e^{-{\sigma }_i\sqrt{d{t}_i}}} \\ 1-q_i=\frac{e^{{\sigma }_i\sqrt{d{t}_i}}-e^{rd{t}_i}}{e^{{\sigma }_i\sqrt{d{t}_i}}-e^{-{\sigma }_i\sqrt{d{t}_i}}} \end{gathered}$$
欧式期权的价值取决于标的股票价格在到期日的分布情况，在到期日前股价的变动路径并不重要。换句话说，唯一重要就是股票在期权有效期内的总方差，总方差等于每个阶段方差的和：
$$(T-t){\sigma }_{Total}^2=\sum _{i=1}^N{\sigma }_i^{2}dt$$
其中年化方差 ${\sigma }_{Total}^2$ 是每阶段方差按照时间加权之后的平均值，且对于欧式期权，阶段波动率的先后顺序并不重要（对于美式期权，阶段波动率的顺序很重要）

在极限条件下，对于一个连续波动率过程 $\sigma (t)$，通过二叉树模型计算的欧式期权价值，将会收敛成为 BSM 公式，对应的隐含波动率 $\sum (t,T)$ 满足：
$${\sum }^2(t,T)=\frac{1}{T-t}{\int }_t^T{\sigma }^2(s)ds$$
其中 $\sigma (t)$ 表示标的资产的前瞻波动率。若知道了隐含波动率的期限结构，即可根据上式倒推出与隐含波动率相应的前瞻波动率。

相类似的，给定连续复利下零息债券无风险收益率 $Y(t,T)$ 的期限结构，在连续极限中，二叉树模型里面，未来每个时间段相对应的远期（前瞻）无风险利率 $r(t)$，都可以用下面的等式计算而得：
$$Y(t,T)=\frac{1}{T-t}{\int }_t^{T}r(s)ds$$