文献阅读--Σ-Δ 小数频率合成器原理
参考文献
本文为阅读相关论文后的笔记。不同类型的频率合成器有不同的优缺点,本文主要是对PLLFS的Σ-Δ小数频率综合器的原理进行记录学习。
论文:
[1] 刘宝宝.Sigma-Delta小数频率综合器中小数分频器研究与设计[D].华侨大学,2012.
[2] 梁佳琦.高精度Σ-Δ小数分频器的研究与设计[D].中国运载火箭技术研究院,2022.DOI:10.27096/d.cnki.ghtdy.2022.000012
[3] 雷旭.900MHz Delta-sigma小数型频率合成器的设计与实现[D].电子科技大学,2017.
博客:
Σ-Δ ADC的高精度数模转化,是如何实现的?
ΣΔ(Sigma-Delta)技术详解(上):离散ΣΔ调制器
Delta-Sigma调制(DSM)技术
一、频率合成器概述
频率合成器他作为无线收发机系统的一个非常关键的模块,它的功能是用于产生本振信号,本振信号是收发机所必需的,其输出的信号的好坏决定了收发机变频信号的优劣,调频范围决定了收发机的收发频率范围,收发机工作的效率受到其频率的切换时间制约,收发机最小信道宽度受限于频率合成器的精度。常用的频率合成器主要可以用以下几种方式来实现:
- 直接模拟式频率合成器(Direct Analog Synthesizer,DAS)
- 直接数字式频率合成器(Direct Digital Synthesizer,DDS)
- 基于锁相环结构的频率合成器(Phase Locked Loop Frequency Synthesizer,PLLFS)
1.1 直接模拟式频率合成器(Direct Analog Synthesizer,DAS)
DAS 是利用一个或者多个不同的晶体振荡器作为基准信号源,它由倍频器、分频器、混频器等模块组成。它具有信号稳定、频率变化速度快,但是它的调试难度较大,而且这种结构的芯片面积以及它的功耗都很大,不适用于当前电路低功耗、小面积的发展趋势,因此 DAS 一般不被使用。
1.2 直接数字式频率合成器(Direct Digital Synthesizer,DDS)
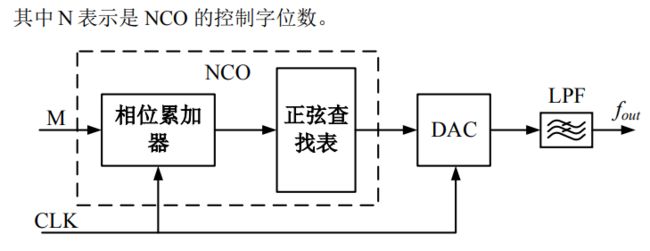
DDS主要由模数转换器(DAC)和数控振荡器(NCO)组成,其中 NCO模块可分为正弦查找表以及相位累加器,结构如图所示。其中,M表示频率控制字,DDS 的输出可以通过调整M 的大小来调节。输入输出频率的关系式为:
f o u t = f o u t ∙ M / 2 N f_{out}=f_{out}\bullet M / 2^{N} fout=fout∙M/2N
1.3 基于锁相环结构的频率合成器(Phase Locked Loop Frequency Synthesizer,PLLFS)
1.3.1 PLLFS简介
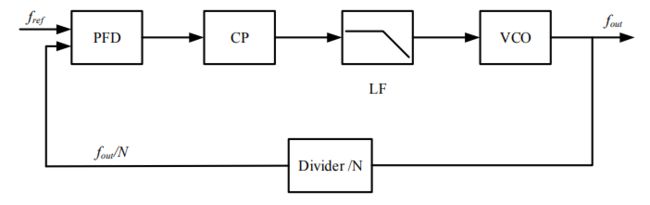
PLLFS 以 PLL 为基础,在传统的 PLL 环路上加入了一个可编程的分频器,这个分频器具有分频比可调节的特点,可以通过调节分频比来改变频率合成器的输出频率。图为 PLLFS 的基本结构。PLLFS 根据分频的形式不同可以分为以下三种结构:整数型频率合成器、小数型频率合成器 和全数字型频率合成器。
1.3.2 PLLFS基本原理
PLLFS 的工作原理如下:环路通过将输入参考频率 f r e f f_{ref} fref与VCO通过分频器处理后的频率 f d i v f_{div} fdiv保持同步,这时VCO的输出频率为参考频率的 N 倍,因此 PLLFS 可以实现对 f r e f f_{ref} fref的倍频功能。DIVIDER 用于实现频率合成器的倍频功能。
PLLFS 子模块主要是鉴频鉴相器(PFD)、电荷泵(CP) 、环路滤波器(LF) 、压控振荡器(VCO)和分频器(DIVIDER)。LF一般采用低通滤波器,主要用于滤波,保证VCO控制电压的稳定;VCO的调谐频率决定了频率合成器的输出频率范围,这个范围理论上越大越好;PFD主要用于比较 f r e f f_{ref} fref和 f d i v f_{div} fdiv的频差和相位差,然后根据差值产生控制CP 充放电的信号UP和DN,CP 的不断充放电会使 VCO的控制电压不断变化,输出频率也一直变化,直到 f r e f f_{ref} fref和 f d i v f_{div} fdiv完全同步,这种状态下的 PLLFS 即为锁定状态。
二、小数型频率合成器
2.1 基本原理
在小数型频率合成器中使用的可编程分频器无法直接实现小数分频功能,可以通过合理的控制可编程分频器的瞬时分频比,用平均值的概念可以认为频率合成器实现了小数分频的功能。双模分频器的分频比由n位累加器控制,当累加器输出y[k]=1 时,双模分频器(N+1)分频,累加器输出y[k]=0 时,则进行N分频,基本结构如图所示。
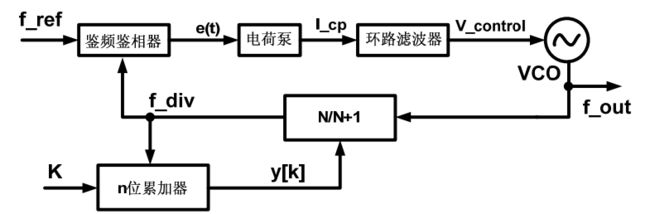
例如: 实现 M = N + α M=N+α M=N+α 分频,其中 0 ≤ α ≤ 1 0≤α≤1 0≤α≤1 为小数部分,则累加器的输入应为 K = α × 2 n K=α×2^n K=α×2n,即在输入时钟 f d i v f_{div} fdiv下,每 K K K个周期,累加器就输出一个 1,其余 ( 2 n − K ) (2^n-K) (2n−K)个周期,累加器则保持 0 状态。当环路锁定时,VCO的输出频率与参考频率满足:
f v c o = M f r e f = ( 2 n − K ) N + K ( N + 1 ) 2 n f r e f = ( N + K 2 n ) f r e f f_{vco}=M f_{ref}=\frac{\left(2^n-K\right) N+K(N+1)}{2^n} f_{r e f}=\left(N+\frac{K}{2^n}\right) f_{r e f} fvco=Mfref=2n(2n−K)N+K(N+1)fref=(N+2nK)fref
实现 f v c o = ( N + α ) f r e f f_{vco}=(N+\alpha) f_{ref} fvco=(N+α)fref 的小数分频
参考频率固定时, 频率分辨率取决于累加器的位数 ( K = 1 ) (K=1) (K=1) :
δ = 1 2 n f r e f \delta=\frac{1}{2^n} f_{ref} δ=2n1fref
小数频率综合器与整数频率综合器最大的区别就是:在锁定状态下,小数频率综合器的瞬态分频比是不停地变化的,从整个周期上看,输出频率的平均值是参考频率的小数倍。但是周期变化的分频比会在压控振荡器控制电压上产生一个叠加在直流电平上的呈现周期性的交流信号,进而导致产生杂散,杂散位于的 ± α ∙ f r e f \pm α \bullet f_{ref} ±α∙fref处,叫做小数杂散。小数杂散是小数频率综合器存在的主要问题
2.2 消除小数杂散的方法
| 结构 | 特点 | 缺陷 |
|---|---|---|
| DAC 相位补偿 | 使用 DAC 产生补偿电压,消除杂散 | DAC 电路的失配 |
| 随机加抖 | 外加数字抖动、随机分频比 | 频率抖动和低频噪声严重 |
| Σ-Δ 调制 | 噪声整形、调制分频比 | 高频量化噪声 |
| 相位插抖 | 使用相位的选择实现小数分频 | 插值引起抖动 |
| 脉冲产生 | 脉冲插入进行倍频操作 | 插值引起抖动 |
三、Σ-Δ 小数频率合成器
Sigma-Delta调制消除杂散是基于Σ-Δ调制器的输出是随机序列,使得双模分频器的分频比亦随机变化,环路的相位误差也具有随机性,则VCO的控制电压只有直流分量,消除了其低频交流成分,达到了消除杂散的目的。基本结构如图所示
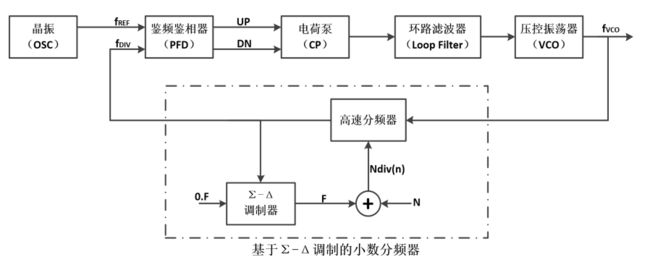
其中Σ-Δ调制器对设置的小数分频值进行调制,输出一系列平均值为小数值的整数分频值。高速分频器受Σ-Δ调制器控制实现不同的分频比。通过这样,Σ-Δ调制器和高速分频器共同将设置的小数分频值量化成不断变化的整数分频值,使其平均值等于设定的小数值。

注:高速分频器、双模分频器
高速分频器的常用结构有两种:2/3 分频器级联的多模分频器和脉冲吞咽分频器。
不论是 2/3 分频器级联的多模分频器还是脉冲吞咽分频器,均需以双模分频器为基础结构进行分频比扩展,双模分频器主要有以下两种技术实现方法:同步逻辑双模分频器、相位切换结构双模分频器
3.1 Σ-Δ调制器
Σ-Δ调制器的作用是将输入模拟信号转换为由二值构成的串行数据。Σ-Δ调制器基于量化和过采样原理,具有噪声整形的作用,能够将量化噪声推向高频,再通过环路滤波器滤除,减少对环路噪声的影响。 同时Σ-Δ调制采用数字电路构成,受工艺的影响较低,因而得到了广泛的应用。
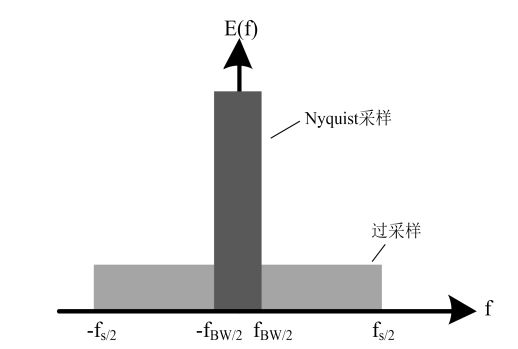
3.1.1 过采样
结论:Nyquist 采样和过采样后的量化噪声功率谱密度对比,可以看出,总噪声功率并未改变,但采用过采样后带内噪声功率大大减小。
3.1.1 噪声整形
一阶 Σ-Δ 调制器由一个积分器和一个量化器构成,如图是其等效模型。输入 x ( n ) x(n) x(n)通过一个积分器和一个量化器得到输出 y ( n ) y(n) y(n), 而量化输出 y ( n ) y(n) y(n) 又通过一个反馈环路跟踪输入 x ( n ) x(n) x(n),可以推得一阶量化器的传递函数为:
Y ( Z ) = Z − 1 X ( Z ) + ( 1 − Z − 1 ) E ( Z ) \mathrm{Y}(\mathrm{Z})=\mathrm{Z}^{-1} \mathrm{X}(\mathrm{Z})+\left(1-\mathrm{Z}^{-1}\right) \mathrm{E}(\mathrm{Z}) Y(Z)=Z−1X(Z)+(1−Z−1)E(Z)
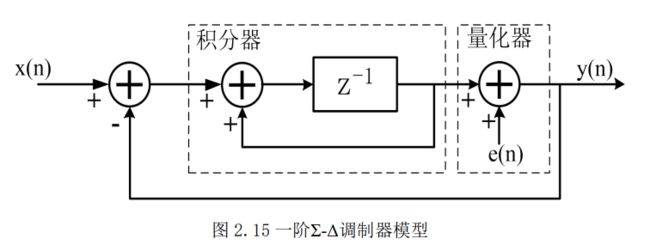
其中, Y ( Z ) 、 X ( Z ) 、 Q ( Z ) Y(Z) 、 X(Z) 、 Q(Z) Y(Z)、X(Z)、Q(Z) 分别为输出信号、输入信号和量化噪声的Z域表示。可以看到,一阶调制器对于输入信号只有一阶延时,对于量化噪声则是一阶高通滤波。其中 X ( Z ) \mathrm{X}(\mathrm{Z}) X(Z) 的系数称为信号传递函数 , Q ( Z ) \mathrm{Q}(\mathrm{Z}) Q(Z) 的系数称为噪声传递函数。因此,数字 Σ-Δ 调制器可以输出完整的输入信号和经过高通滤波的量化噪声。Σ-Δ 调制器对量化噪声的滤波作用即噪声整形。

3.2 高阶 Σ-Δ调制器
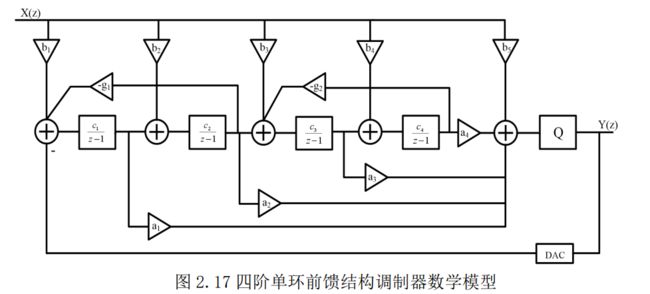
以一阶Σ-Δ调制器作为基本单元,可以构成高阶的Σ-Δ调制器,主要分为单环(SingleLoop)结构和多级噪声级联(Multi Stage Noise Shaping,MASH)结构。高阶结构能调制输出更加随机的分频比,理论研究表明,调制器的阶数越高,其噪声整形效果越好。这部分就不详细展开了,深入了解请阅读相关文献。
3.2.1 单环Σ-Δ调制器
3.2.2 多级噪声级联结构Σ-Δ调制器
多级噪声级联结构Σ-Δ调制器由一阶调制器级联而成,常见类型有 MASH 1-1-1、MASH 1-1-1-1 和 MASH 1-2 等。图为 MASH 1-1-1 结构,18 位的线性反馈移位寄存器(LFSR)置于小数最低位,从而来生成伪随机序列,破坏调制的周期性。

MASH 1-1-1传输函数为:
Y ( z ) = z − 2 Y 1 ( z ) + z − 1 ( 1 − z − 1 ) Y 2 ( z ) + ( 1 − z − 1 ) 2 Y 3 ( z ) ⇒ Y ( z ) = z − 2 X ( z ) + ( 1 − z − 1 ) 3 E 3 ( z ) + ( 1 − z − 1 ) 2 D ( z ) 2 M \begin{aligned} & Y(z)=z^{-2} Y_1(z)+z^{-1}\left(1-z^{-1}\right) Y_2(z)+\left(1-z^{-1}\right)^2 Y_3(z) \\ & \Rightarrow Y(z)=z^{-2} X(z)+\left(1-z^{-1}\right)^3 E_3(z)+\left(1-z^{-1}\right)^2 \frac{D(z)}{2^M} \end{aligned} Y(z)=z−2Y1(z)+z−1(1−z−1)Y2(z)+(1−z−1)2Y3(z)⇒Y(z)=z−2X(z)+(1−z−1)3E3(z)+(1−z−1)22MD(z)
总结
阐述了小数型频率合成器的基本原理和常见结构。为解决合成器的小数杂散问题引入Σ-Δ调制,介绍了Σ-Δ调制调制器的基本原理和作用。