数据结构期末复习(3)栈和队列
堆栈(stack)
堆栈(stack)是一种基于后进先出(LIFO,Last In First Out)原则的数据结构。它模拟了现实生活中的堆栈,类似于一摞盘子或一堆书。
堆栈有两个基本操作:入栈(push)和出栈(pop)。
- 入栈(push):将新元素添加到堆栈的顶部。新元素成为当前堆栈的最上面一个元素。
- 出栈(pop):从堆栈的顶部移除最上面的元素,并返回该元素的值。
除了这两个基本操作外,堆栈还可以支持其他常用操作,例如:
- 栈顶(top):获取堆栈的顶部元素,但不移除它。
- 判空(isEmpty):检查堆栈是否为空。
- 获取大小(size):获取堆栈中元素的数量。
实际上,堆栈可以通过数组或链表来实现。
使用数组实现的堆栈称为顺序堆栈(array-based stack)。在顺序堆栈中,数组的末尾被用作栈顶,每次入栈操作都会将元素放置在数组末尾,而出栈操作则会从数组末尾移除元素。

使用链表实现的堆栈称为链式堆栈(linked stack)。在链式堆栈中,每个节点包含一个元素和一个指向下一个节点的引用。入栈操作将在链表头部插入新节点,而出栈操作则会移除链表头部的节点。
堆栈在计算机科学中有广泛的应用。例如,在编程中,堆栈常用于函数调用的过程中,每当一个函数被调用时,其相关信息(如参数、局部变量等)都会被压入堆栈中,当函数执行完毕后,这些信息又会被弹出堆栈。这种方式使得程序可以追踪函数的嵌套调用,并正确恢复执行状态。
堆栈还被用于解决许多其他问题,如括号匹配、表达式求值、深度优先搜索算法、回溯算法等。其简单性和高效性使得堆栈成为一种重要的数据结构。
后缀表达式
堆栈的抽象数据描述
堆栈(stack)是一种抽象数据类型(ADT),用于描述具有后进先出(LIFO,Last In First Out)特性的数据结构。它定义了以下操作:
- 初始化(Initialize):创建一个空的堆栈。
- 入栈(Push):将一个新元素添加到堆栈的顶部。
- 出栈(Pop):从堆栈的顶部移除最上面的元素,并返回该元素的值。
- 栈顶(Top):获取堆栈的顶部元素,但不移除它。
- 判空(IsEmpty):检查堆栈是否为空。
- 获取大小(Size):获取堆栈中元素的数量。
这些操作定义了堆栈的基本行为和特点。使用这些操作,可以实现各种具体的堆栈实现,如基于数组或链表的实现。

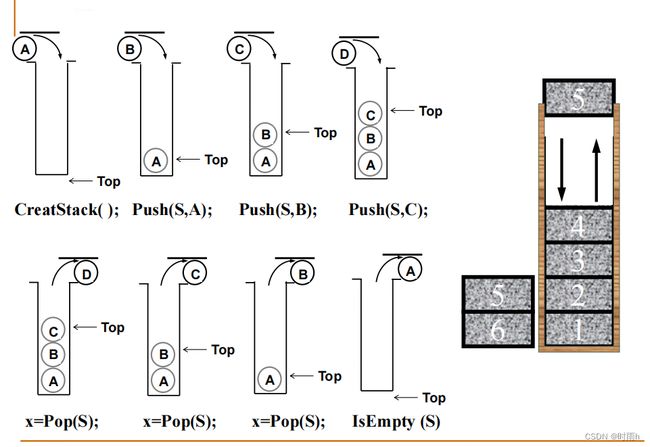

[例] 如果三个字符按ABC顺序压入堆栈
• ABC的所有排列都可能
是出栈的序列吗?
• 可以产生CAB这样的序
列吗?
在递归的过程中,我们维护一个栈和一个指向原始字符序列的指针。如果当前栈顶元素与指针指向的元素相同,则可以将其出栈;否则,需要将指针指向的元素入栈。当原始字符序列中的所有元素都已经被入栈后,我们可以逐步将栈中的元素出栈,从而得到一种可能的出栈序列。
使用上述方法,我们可以得到所有可能的出栈序列。如果其中包含了以CAB为开头的序列,那么就说明CAB是一种可能的出栈序列。否则,就不能产生CAB这样的序列。
总结:按照ABC的顺序依次压入堆栈,其所有可能的出栈序列有6种,分别是ABC、ACB、BAC、BCA、CBA和CAB。因此,CAB是一种可能的出栈序列。
栈的顺序存储实现
#define MAXSIZE 100 // 定义栈的最大容量
typedef struct {
ElementType data[MAXSIZE]; // 用数组存储栈元素
int top; // 栈顶指针,指向当前栈顶元素的位置
} Stack;
// 初始化栈
void InitStack(Stack *S) {
S->top = -1; // 初始化栈顶指针为-1,表示空栈
}
// 判断栈是否为空
int IsEmpty(Stack *S) {
return (S->top == -1);
}
// 判断栈是否已满
int IsFull(Stack *S) {
return (S->top == MAXSIZE - 1);
}
// 入栈操作
void Push(Stack *S, ElementType item) {
if (IsFull(S)) {
printf("Stack is full. Cannot push element %d.\n", item);
} else {
S->data[++(S->top)] = item;
}
}
// 出栈操作
ElementType Pop(Stack *S) {
if (IsEmpty(S)) {
printf("Stack is empty. Cannot pop element.\n");
return ERROR; // ERROR可以是一个预定义的错误值
} else {
return S->data[(S->top)--];
}
}
// 获取栈顶元素
ElementType GetTop(Stack *S) {
if (IsEmpty(S)) {
printf("Stack is empty. No top element.\n");
return ERROR;
} else {
return S->data[S->top];
}
}
堆栈的链式存储实现
typedef struct StackNode {
ElementType data; // 数据域
struct StackNode *next; // 指针域,指向下一个节点
} StackNode;
typedef struct {
StackNode *top; // 栈顶指针,指向当前栈顶元素
} LinkedStack;
// 初始化栈
void InitStack(LinkedStack *S) {
S->top = NULL; // 初始化栈顶指针为空,表示空栈
}
// 判断栈是否为空
int IsEmpty(LinkedStack *S) {
return (S->top == NULL);
}
// 入栈操作
void Push(LinkedStack *S, ElementType item) {
StackNode *newNode = (StackNode *)malloc(sizeof(StackNode)); // 创建新节点
newNode->data = item; // 设置新节点的数据域为要入栈的元素
newNode->next = S->top; // 将新节点插入到栈顶
S->top = newNode; // 更新栈顶指针
}
// 出栈操作
ElementType Pop(LinkedStack *S) {
if (IsEmpty(S)) {
printf("Stack is empty. Cannot pop element.\n");
return ERROR; // ERROR可以是一个预定义的错误值
} else {
StackNode *temp = S->top; // 保存当前栈顶节点
ElementType item = temp->data; // 获取栈顶元素的值
S->top = temp->next; // 更新栈顶指针
free(temp); // 释放原栈顶节点
return item;
}
}
// 获取栈顶元素
ElementType GetTop(LinkedStack *S) {
if (IsEmpty(S)) {
printf("Stack is empty. No top element.\n");
return ERROR;
} else {
return S->top->data;
}
}
堆栈应用:表达式求值
当涉及到表达式求值时,我们可以考虑使用堆栈的应用。以下是一个更复杂的例子来演示如何使用堆栈进行中缀表达式的求值。
假设我们要求解的表达式为中缀表达式:(3 + 4) * 5 - 6 / 2
- 创建一个空栈和运算符优先级字典。
- 从左到右遍历中缀表达式中的每个元素。
- 如果当前元素是数字,则将其转换为整数并直接入栈。
- 如果当前元素是运算符,进行以下操作:
- 如果栈为空或者栈顶元素是左括号"(",则将当前运算符入栈。
- 如果栈不为空,并且当前运算符的优先级大于栈顶运算符的优先级,则将当前运算符入栈。
- 如果栈不为空,并且当前运算符的优先级小于等于栈顶运算符的优先级,则弹出栈顶运算符并进行计算,并将计算结果入栈。重复此步骤直到满足条件,然后将当前运算符入栈。
- 如果当前元素是右括号")“,则弹出栈顶运算符并进行计算,直到遇到左括号”(“。左括号”("从栈中弹出,但不进行计算。
- 当遍历完中缀表达式后,将栈中剩余的运算符依次弹出并进行计算。
- 栈中仅剩下一个元素,即为表达式的计算结果。
以下是对中缀表达式(3 + 4) * 5 - 6 / 2求值的具体步骤:
- 创建一个空栈和运算符优先级字典(加法和减法优先级为1,乘法和除法优先级为2)。
- 遍历到"(",将其入栈。
- 遍历到3,将其转换为整数并入栈。
- 遍历到"+“,栈顶是”(“,将”+"入栈。
- 遍历到4,将其转换为整数并入栈。
- 遍历到")“,弹出栈顶运算符”+"并进行计算,得到3+4=7,并将计算结果7入栈。
- 遍历到"“,栈顶元素是7,优先级大于”“,将”*"入栈。
- 遍历到5,将其转换为整数并入栈。
- 遍历到"-“,栈顶元素是”“,优先级小于等于”-“,弹出栈顶运算符”"并进行计算,得到7*5=35,并将计算结果35入栈。
- 遍历到6,将其转换为整数并入栈。
- 遍历到"/“,栈顶元素是6,优先级小于等于”/“,弹出栈顶运算符”/"并进行计算,得到6/2=3,并将计算结果3入栈。
- 遍历完中缀表达式后,栈中仅剩下一个元素35-3,即为表达式的计算结果。
因此,中缀表达式(3 + 4) * 5 - 6 / 2的值为32。
中缀表达式如何转换为后缀表达式
将中缀表达式转换为后缀表达式的一种常用方法是使用栈。
以下是转换过程的步骤:
- 创建一个空栈和一个空列表,用于存储后缀表达式。
- 从左到右遍历中缀表达式中的每个元素。
- 如果当前元素是数字或字母,则直接添加到后缀表达式列表的末尾。
- 如果当前元素是左括号"(",则将其入栈。
- 如果当前元素是右括号")“,则将栈中的元素弹出并添加到后缀表达式列表,直到遇到左括号”("。然后将左括号从栈中弹出,但不将其添加到后缀表达式列表中。
- 如果当前元素是运算符(如"+", “-”, “*”, "/"等),则进行以下操作:
- 如果栈为空,则将当前运算符入栈。
- 如果栈不为空,并且栈顶元素是左括号"(",则将当前运算符入栈。
- 如果栈不为空,并且当前运算符的优先级小于等于栈顶运算符的优先级,则将栈顶运算符弹出并添加到后缀表达式列表,重复此步骤直到满足条件,然后将当前运算符入栈。
- 如果栈不为空,并且当前运算符的优先级大于栈顶运算符的优先级,则将当前运算符入栈。
- 当遍历完中缀表达式后,将栈中剩余的运算符依次弹出并添加到后缀表达式列表。
- 后缀表达式列表即为转换后的后缀表达式。
以下是一个示例:
中缀表达式:2 + 3 * 4
转换过程:
- 遍历到2,直接添加到后缀表达式列表。
- 遍历到+,栈为空,将其入栈。
- 遍历到3,直接添加到后缀表达式列表。
- 遍历到*,栈不为空,栈顶是+,将*入栈。
- 遍历到4,直接添加到后缀表达式列表。
- 遍历完中缀表达式,将栈中剩余的运算符+和*依次弹出并添加到后缀表达式列表。
转换后的后缀表达式:2 3 4 * +
因此,中缀表达式2 + 3 * 4可以转换为后缀表达式2 3 4 * +。
队列
队列(Queue)是一种线性数据结构,它具有先进先出(FIFO)的特性。队列可以看作是一个有头有尾的队伍,新元素被添加到队尾,而删除元素则从队头进行。在队列中,数据元素的插入操作叫做入队(enqueue),删除操作则叫做出队(dequeue)。队列常用于操作系统调度、消息传递、任务处理等场景。
队列可以使用数组或者链表来实现。使用数组实现时,需要维护队头和队尾指针,以便快速进行入队和出队操作;使用链表实现时,则只需要维护队头和队尾节点即可。
在队列中,还有一些其他的操作,例如获取队头元素(peek)、判断队列是否为空(isEmpty)等。同时,队列还可以分为普通队列和优先级队列,后者可以根据元素的优先级来进行出队操作。


队列的基本操作
- 初始化队列(initQueue):创建一个空队列,并进行必要的初始化工作,例如设置队头和队尾指针为 NULL。
void initQueue(Queue *q) {
q->front = q->rear = NULL;
}
- 入队操作(enqueue):将新元素插入到队列的队尾,使其成为新的队尾元素。
void enqueue(Queue *q, int data) {
Node *newNode = (Node*)malloc(sizeof(Node));
newNode->data = data;
newNode->next = NULL;
if (q->front == NULL) { // 如果队列为空,新节点同时也成为队头节点
q->front = q->rear = newNode;
} else {
q->rear->next = newNode; // 将新节点插入到队尾
q->rear = newNode; // 更新队尾指针
}
}
- 出队操作(dequeue):删除队列的队头元素,并返回该元素的值。如果队列为空,则出队操作失败。
int dequeue(Queue *q) {
if (q->front == NULL) { // 如果队列为空,出队失败
printf("Queue is empty!\n");
return -1;
}
int data = q->front->data; // 获取队头元素的值
Node *temp = q->front;
q->front = temp->next; // 将队头指针指向下一个节点
free(temp); // 释放原队头节点的内存空间
if (q->front == NULL) { // 如果队列为空,更新队尾指针
q->rear = NULL;
}
return data;
}
- 获取队头元素(front):返回队列的队头元素的值,但不删除该元素。
int front(Queue *q) {
if (q->front == NULL) { // 如果队列为空,返回错误值
printf("Queue is empty!\n");
return -1;
}
return q->front->data; // 返回队头元素的值
}
- 判断队列是否为空(isEmpty):检查队列是否为空,即判断队列的队头指针是否为 NULL。
bool isEmpty(Queue *q) {
return (q->front == NULL); // 如果队头指针为空,则队列为空
}
- 清空队列(clearQueue):释放队列中所有节点的内存空间,并将队头和队尾指针设置为 NULL,使队列变为空队列。
void clearQueue(Queue *q) {
Node *temp;
while (q->front != NULL) {
temp = q->front;
q->front = temp->next;
free(temp);
}
q->rear = NULL; // 将队尾指针置为 NULL
}
这些是队列的详细操作,可以根据实际需求进行使用和扩展。注意,在使用完队列后,需要调用清空队列的函数来释放内存空间。
队列的存储结构

队列有两种常见的存储结构:数组(顺序队列)和链表(链式队列)。
- 数组实现的顺序队列:
顺序队列使用数组作为底层存储结构,通过数组的下标来表示元素在队列中的位置。需要两个指针,分别指向队头和队尾元素。队头指针指向队列的第一个元素,队尾指针指向队列最后一个元素的下一个位置。
优点:简单、易于实现和理解,占用连续的内存空间,访问元素方便。
缺点:如果队列长度不固定,会浪费一部分空间。
- 链表实现的链式队列:
链式队列使用链表作为底层存储结构,每个节点包含数据元素和指向下一个节点的指针。需要两个指针,分别指向队头和队尾节点。
优点:没有长度限制,可以动态地分配内存,节省空间。
缺点:访问元素时需要遍历链表,稍微复杂一些。
无论是顺序队列还是链式队列,它们都支持队列的基本操作,如入队、出队、获取队头元素、判断队列是否为空等。选择使用哪种存储结构取决于具体的需求和使用场景。
队列的假溢出
队列的假溢出(False Overflow)是指当队列未满时,仍然无法插入新元素的情况。这通常发生在使用数组实现的循环队列中,当队列尾指针 rear 指向数组的最后一个位置后,如果队头指针 front 也指向数组的最后一个位置,则队列被认为已满。
举个例子,假设有一个长度为5的循环队列,初始时 front = rear = 0,队列中已经存在3个元素。此时,队列的状态如下:
[1, 2, 3, _, _]
^ ^
front rear
如果此时要入队一个新元素,即使队列中还有空闲位置,也无法插入新元素,因为 rear 指针已经指向数组的最后一个位置,而 front 也指向了同样的位置,导致假溢出。
解决假溢出问题的方法是使用循环队列。当 rear 指针到达数组末尾时,将其重新指向数组的起始位置,使得队列能够循环利用数组空间。
在上述的例子中,如果要入队一个新元素,可以将 rear 指针从数组末尾位置移到数组起始位置,然后插入新元素:
[_, _, 3, 4, _]
^ ^
rear front
这样,假溢出的问题就得到了解决。循环队列的实现可以通过取模运算来实现,以保证 rear 和 front 指针始终在合法范围内。
循环队列

循环队列是一种使用数组实现的队列,通过循环利用数组的空间来解决假溢出的问题。循环队列的关键是要使用取模运算来计算队列的下标,以保证队列的循环性质。
循环队列通常由以下几个属性组成:
- 一个固定大小的数组,用于存储队列元素。
- 两个指针,分别指向队头和队尾元素在数组中的位置。
- 一个计数器,用于记录当前队列中元素的个数。
下面是循环队列的一些基本操作:
- 初始化队列(initQueue):创建一个空队列,并进行必要的初始化工作,例如设置队头和队尾指针为初始位置,计数器为零。
void initQueue(CircularQueue *q) {
q->front = 0;
q->rear = 0;
q->count = 0;
}
- 入队操作(enqueue):将新元素插入到队列的队尾,并更新队尾指针和计数器。
void enqueue(CircularQueue *q, int data) {
if (q->count == MAX_SIZE) { // 队列已满,无法插入新元素
printf("Queue is full!\n");
return;
}
q->data[q->rear] = data; // 插入新元素到队尾位置
q->rear = (q->rear + 1) % MAX_SIZE; // 更新队尾指针
q->count++; // 增加计数器
}
- 出队操作(dequeue):删除队列的队头元素,并返回该元素的值。如果队列为空,则出队操作失败。
int dequeue(CircularQueue *q) {
if (q->count == 0) { // 队列为空,无法删除元素
printf("Queue is empty!\n");
return -1;
}
int data = q->data[q->front]; // 获取队头元素的值
q->front = (q->front + 1) % MAX_SIZE; // 更新队头指针
q->count--; // 减少计数器
return data;
}
- 获取队头元素(front):返回队列的队头元素的值,但不删除该元素。
int front(CircularQueue *q) {
if (q->count == 0) { // 队列为空,返回错误值
printf("Queue is empty!\n");
return -1;
}
return q->data[q->front]; // 返回队头元素的值
}
- 判断队列是否为空(isEmpty):检查队列是否为空,即判断计数器是否为零。
bool isEmpty(CircularQueue *q) {
return (q->count == 0); // 如果计数器为零,则队列为空
}
循环队列的实现通过使用取模运算来循环利用数组空间,使得队列能够重复使用数组中的位置。这种实现方式可以有效地解决假溢出问题,并且在时间复杂度上具有较好的性能。
队伍的链式存储结构
队列的链式存储结构使用链表来实现队列的基本操作。每个节点包含一个数据元素和一个指向下一个节点的指针。队列的头部指向链表的第一个节点,队列的尾部指向链表的最后一个节点。
链式存储结构的队列相比于数组实现的循环队列,具有更灵活的空间管理和动态扩展的能力。下面是队列链式存储结构的一些基本操作:
- 定义队列节点结构体:
typedef struct Node {
int data;
struct Node* next;
} Node;
- 初始化队列(initQueue):创建一个空队列,并进行必要的初始化工作,例如设置头部和尾部指针为空。
void initQueue(LinkedQueue* q) {
q->front = NULL;
q->rear = NULL;
}
- 入队操作(enqueue):创建一个新节点,并将其插入到队列的尾部。更新尾部指针。
void enqueue(LinkedQueue* q, int data) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->data = data;
newNode->next = NULL;
if (isEmpty(q)) { // 队列为空,更新头部指针
q->front = newNode;
} else { // 队列不为空,更新尾部指针
q->rear->next = newNode;
}
q->rear = newNode; // 更新尾部指针
}
- 出队操作(dequeue):删除队列的头部节点,并返回该节点的值。更新头部指针。
int dequeue(LinkedQueue* q) {
if (isEmpty(q)) { // 队列为空,出队操作失败
printf("Queue is empty!\n");
return -1;
}
Node* temp = q->front; // 保存头部节点
int data = temp->data; // 获取头部节点的值
q->front = q->front->next; // 更新头部指针
free(temp); // 释放头部节点的内存
if (isEmpty(q)) { // 队列为空,更新尾部指针
q->rear = NULL;
}
return data;
}
- 获取队头元素(front):返回队列的头部节点的值,但不删除该节点。
int front(LinkedQueue* q) {
if (isEmpty(q)) { // 队列为空,返回错误值
printf("Queue is empty!\n");
return -1;
}
return q->front->data; // 返回头部节点的值
}
- 判断队列是否为空(isEmpty):检查队列是否为空,即判断头部指针是否为空。
bool isEmpty(LinkedQueue* q) {
return (q->front == NULL);
}
需要注意的是,在使用链式存储结构的队列时,需要小心内存管理,确保在不需要的节点时进行及时的释放操作,以防止内存泄漏。
当使用链式存储结构实现队列时,可以根据需要进行进一步的扩展和优化。下面是一些可能的操作和注意事项:
-
判断队列是否已满(isFull):由于链式存储结构没有固定大小的限制,所以一般情况下不需要判断队列是否已满。但如果你想设置一个最大长度,可以通过计数器或者限制节点数量来判断队列是否已满。
-
清空队列(clearQueue):释放所有节点的内存,并将头部和尾部指针都置为空。
void clearQueue(LinkedQueue* q) {
while (!isEmpty(q)) {
dequeue(q);
}
// 重置头部和尾部指针
q->front = NULL;
q->rear = NULL;
}
- 遍历队列(traverseQueue):从队列的头部开始,依次访问每个节点的值。
void traverseQueue(LinkedQueue* q) {
if (isEmpty(q)) {
printf("Queue is empty!\n");
return;
}
Node* current = q->front;
while (current != NULL) {
printf("%d ", current->data);
current = current->next;
}
printf("\n");
}
-
动态扩展队列:链式存储结构的队列天然具备动态扩展的能力。当队列需要存储更多元素时,只需创建新的节点并添加到尾部即可。这样可以避免数组存储结构中固定大小的限制。
-
内存管理:在使用链式存储结构时,需要注意及时释放不再需要的节点的内存,以防止内存泄漏。在出队操作时,需要释放被删除节点的内存。在清空队列或销毁队列时,需要释放所有节点的内存。
下面是一个完整的链式存储结构的队列示例(使用C语言实现):
#include 




















