数学知识：约数

---

前言

复习acwing算法基础课的内容，本篇为讲解数学知识：约数，关于时间复杂度：目前博主不太会计算，先鸽了，日后一定补上。

---

一、约数，质因子

约数（又称因数）是指若整数a除以整数b(b≠0)除得的商正好是整数而没有余数，就说a能被b整除，或b能整除a，其中a称为b的倍数，b称为a的约数。

质因子就是质数的因子，也称质因数或质约数。 255的因子有1 、3、5、15、17、51、85、255。其中是质数的是1、3、5、17 所以255的质因子就是1、3、5、17

---

二、例题，代码

AcWing 869. 试除法求约数

本题链接：AcWing 869. 试除法求约数
本博客提供本题截图：

本题解析

用到了vector，用法见：STL—vector

AC代码

#include 
#include 
#include 

using namespace std;

vector<int> get_divisors(int x)
{
    vector<int> res;
    for (int i = 1; i <= x / i; i ++ )
        if (x % i == 0)
        {
            res.push_back(i);
            if (i != x / i) res.push_back(x / i);
        }
    sort(res.begin(), res.end());
    return res;
}

int main()
{
    int n;
    cin >> n;

    while (n -- )
    {
        int x;
        cin >> x;
        auto res = get_divisors(x);

        for (auto x : res) cout << x << ' ';
        cout << endl;
    }

    return 0;
}

AcWing 870. 约数个数

本题链接：AcWing 870. 约数个数
本博客提供本题截图：

本题解析

约数个数计算公式：首先把这个数写成质因数的乘积的形式：

这个数的约数的个数就是：

用到了unordered_map，用法同map，见：STL—map

AC代码

#include 
#include 
#include 
#include 

using namespace std;

typedef long long LL;

const int N = 110, mod = 1e9 + 7;

int main()
{
    int n;
    cin >> n;

    unordered_map<int, int> primes;

    while (n -- )
    {
        int x;
        cin >> x;

        for (int i = 2; i <= x / i; i ++ )
            while (x % i == 0)
            {
                x /= i;
                primes[i] ++ ;
            }

        if (x > 1) primes[x] ++ ;
    }

    LL res = 1;
    for (auto p : primes) res = res * (p.second + 1) % mod;

    cout << res << endl;

    return 0;
}

AcWing 871. 约数之和

本题链接：AcWing 871. 约数之和
本博客提供本题截图：

本题解析

计算约数之和的公式：首先把这个数写成质因数的乘积的形式：

这个数的约数之和就是：

如何凑出：

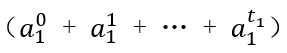
利用：

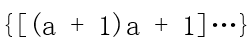
AC代码

#include 
#include 
#include 
#include 

using namespace std;

typedef long long LL;

const int N = 110, mod = 1e9 + 7;

int main()
{
    int n;
    cin >> n;

    unordered_map<int, int> primes;

    while (n -- )
    {
        int x;
        cin >> x;

        for (int i = 2; i <= x / i; i ++ )
            while (x % i == 0)
            {
                x /= i;
                primes[i] ++ ;
            }

        if (x > 1) primes[x] ++ ;
    }

    LL res = 1;
    for (auto p : primes)
    {
        LL a = p.first, b = p.second;
        LL t = 1;
        while (b -- ) t = (t * a + 1) % mod;
        res = res * t % mod;
    }

    cout << res << endl;

    return 0;
}

AcWing 872. 最大公约数

本题链接：AcWing 872. 最大公约数
本博客提供本题截图：

本题解析

求最大公约数模板：（需要背过）

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

AC代码

#include 
#include 

using namespace std;


int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}


int main()
{
    int n;
    cin >> n;
    while (n -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        printf("%d\n", gcd(a, b));
    }

    return 0;
}

---

三、时间复杂度

关于约数各步操作的时间复杂度以及证明，后续会给出详细的说明以及证明过程，目前先鸽了。