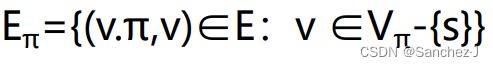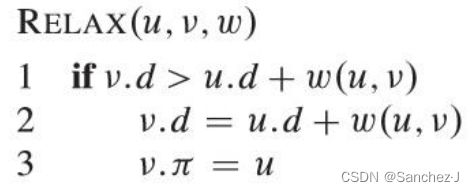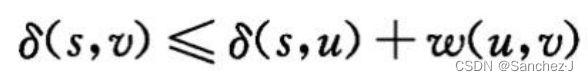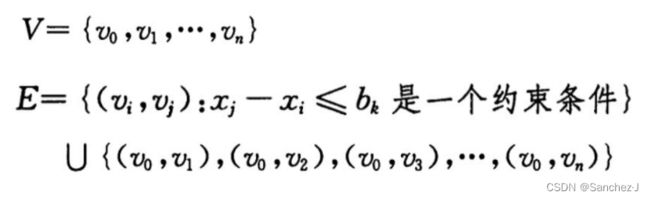算法导论复习——CHP24 单源最短路

        单源最短路径问题： 给定一个图G =(V,E)，找出从给定的源点s∈V到其它每个结点v∈V的最短路径。

        这样最短路径具有最优子结构性：两个结点之间的最短路径的任何子路径都是最短的。

        基本概念

        负权边：权重为负值的边称为负权重的边。 如果存在负权重的边，则有可能存在权重为负值的环路， 而造成图中最短路径无定义（路径的权重为-∞）。

        环路：最短路不应包含环路。

        简单路径：不包含环路的路径称为简单路径。 对任何简单路径最多包含|V|-1条边和|V|个结点。 不失一般性，假设后续算法寻找的最短路径都不包含环路。

        前驱节点：v.π

        前驱子图：,其中，

终止时，前驱子图是一颗最短路径树（包含了从源结点s到每个可以从s到达的结点的一条最短路径）

        松弛操作（Relax）

        最短路径估计 

        对于每个结点v，维持一个属性v.d，记录从源点s到结点v的最短路径权重的上界。

        松弛 

        首先测试一下是否可以对从s到v的最短路径进行改善。如果可以改善，则v.d更新为新的最短路径估计值，v的前驱v.π更新为新的前驱结点。其中，测试指对s到v所经过的最后一个中 间结点u，按下列方式计算从s出发， 经过u而到达v的路径的权重： 将从结点s到结点u之间最短路 径加上结点u到v之间的边的权重， 然后与当前的s到v的最短路径估计 v.d进行比较，看有没有变小。如果 变小，则对v.d和v.π进行更新—— 这一操作就称为“松弛”

        

        三角形不等式

        设G=(V,E)为一个带权重的有向图，其权重函数为 ω:E→R，设其源结点为s。那么对于所有的边(u,v)∈E，有：

         上界性质

        设G=(V,E)为一个带权重的有向图，其权重函数为 ω:E→R，设其源结点为s。对于所有的结点v∈V，v.d ≥ δ(s,v)，并且该不变式在对图G的边进行任何次序的松弛过程中都保持成立，而一 旦v.d取得其下界 δ(s,v)后，将不再发生变化。

        非路径性质

        给定一个带权重的有向图G=(V,E)，其权重函数 为ω:E→R。假定从源结点s到给定点v之间不存在路径，则该图在初始化后，有 v.d≥δ(s,v)=∞， 并且该等式作为不变式一直维持到图G的所有松弛操作结束。

        收敛性质

        设G=(V,E)为一个带权重的有向图，其权重函 数为ω:E→R。设s∈V为某个源结点， 为图G中的 一条最短路径（u，v∈V）。 如果在对边(u,v)进行松弛操作 之前的某时刻有u.d=δ(s,u)，则在该松弛操作之后的所有时刻 有v.d=δ(s,v)

        路径松弛性质

        设G=(V,E)为一个带权重的有向图，其权重函数为ω:E→R。设s∈V为某个源结点，考虑从源结点s到结点vk 的任意一条最短路径p=，v0=s。 如果图G进行了一系列边的松弛操作，其中包括对 边(v0 ,v1 )、 (v1 ,v2 )、…、 (vk-1 ,vk )按照所列次序而进行的松弛操作，则在所有这些松弛操作之后，有vk .d=δ(s,vk )，并且在此之后该等式一直保持。

Bellman-Ford算法

        可以有负权边，不能有负权环。

        可以判断负权环。

        

        时间复杂度O(VE) 

        Dijkstra算法

                该算法要求所有边的权重均为非负值，即对于所有的边 (u,v)∈E，ω(u,v)≥0。

                是一个贪心算法：每次总是选择 V - S 集合中最短路径估计值最小的结点加入S中

                

                时间复杂度分析:

                根据算法的处理规则，每个结点 u 仅被加入集合S一次，邻接链表Adj[u]中的每条边在整个运行期间也只被检查一次。因此算法第7-8行的for循环执行次数总共为 |E| 次（即松弛判定总次数）。         

                Dijkstra算法的总运行时间依赖于最小优先队列Q的实现:

                如果用线性数组(无序或者按序插入)实现，每次找d最小的结点u需要 O(V)的时间，所以算法的总运行时间为O(V * V + E)=。

                如果用二叉堆实现，每次找d最小的结点u需要O(lgV )的时间，所以 算法的总运行时间为O((V+E)lgV )。

                如果用斐波那契堆实现，算法的总运行时间可以改善至O(VlgV+E )。

应用——差分约束系统

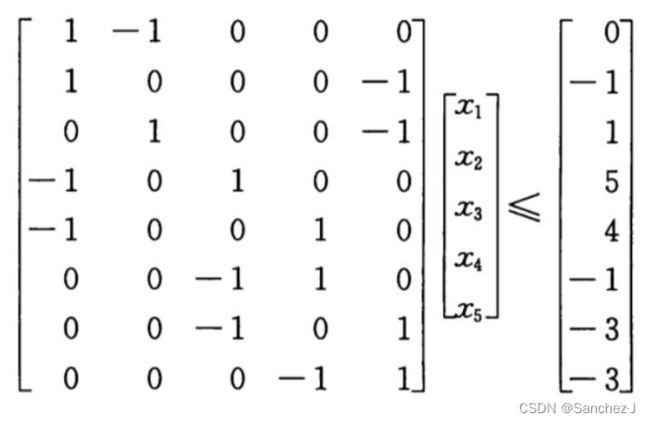
        差分约束系统：在一个差分约束系统中，线性规划矩阵A的每一行包括一个 1 和一个 -1 ，其它所有项皆为0。由Ax≤b给出的约束条件形式上是m个涉及n个变量的差额限制条件(difference constraints)，每个约束条件是以下简单的线性不等关系：

        

如：

现在问题是，如何找出一组解？

引理 

        设向量x=(x1 ,x2 ,…,xn)为差分约束系统Ax≤b的 一个解，设d为任意常数，则x+d=(x1+d,x2+d,…, xn+d) 也是个该差分约束系统的一个解。

差分约束系统的求解可以转化到图的问题上 ：

约束图

        在一个 Ax ≤b 的差分约束系统中，将m╳n的矩阵A看成是一 张有n个结点和m条边构成的图的邻接矩阵的转置。

        定义如下：

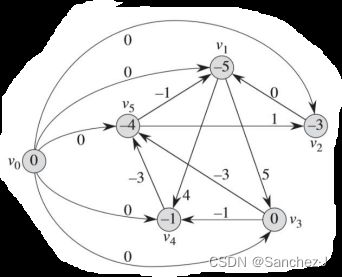
        对给定的差分约束系统Ax≤b，其对应的约束图是一个带权重的有向图G=(V,E)，这里， 每条有向边对应一个不等式，(v0 ,vi)是从新增的v0到其他所有结点的边

                 

        如果 xj - xi ≤ bk是一个差分约束条件，则边(vi,vj) 的权重记为 ω(vi, vj) = bk，而从v0出发到其他结点的边的权重ω(v0 ,vj)=0。 

定理 

        给定差分约束系统Ax≤b，设G=(V,E)是该差分约束系统所对应的约束图。

        (1) 如果图G不包含权重为负值的回路，则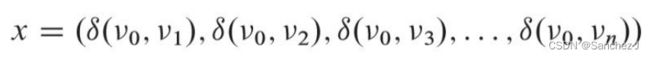是该系统的一个可行解。

        (2) 如果图G包含权重为负值的回路，则该系统没有可行解。

因为可能需要判断负环，所以一般用Bellman-Ford算法