pytorch入门:权重正则化,Dropout正则化,BN ,权重初始化
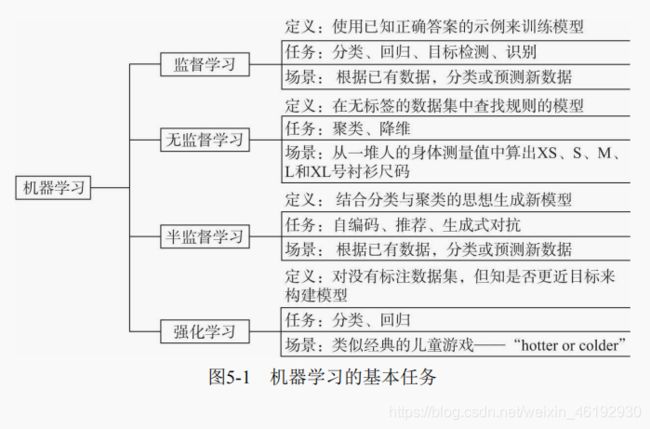
机器学习基础
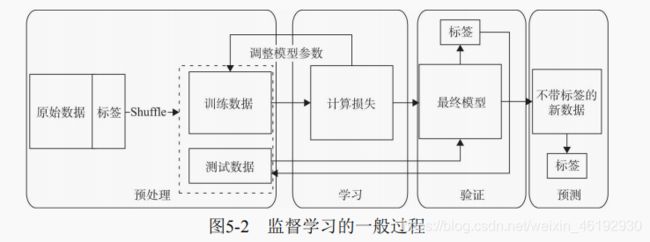
监督学习
给定学习目标(标签),让预测值与目标更加接近。主要是 传统的二分类,多分类,多标签分类,还有新的目标检测,目标识别,图形分割等
无监督学习
没有标签的数据,通过推断输入数据中的结构来建模,模型包括关联学习,降维,聚类等
半监督学习
这个就是前两者的结合,使用大量的没标记的数据,同时由部分使用标记数据进行模式识别。自编码器就是一种半监督学习,生成的目标就是未经修改的输入,语言处理中根据给定文本中的次预测下一个词就是一个例子。
还有对抗生成网络,给定一些真的图片或语音,通过对抗生成网络生成一些与真图片或是语音逼真的图形或语音。
强化学习
强化学习是多学科多领域交叉的一个产物,主要包含四个元素,智能体,环境状态,行动和奖励。强化学习的目的就是获得更多的累计奖励。学习过程就是试探评价的过程,智能体选择一个动作应用于环境,然后得到强化信号(奖励或惩罚),智能体再根据强化信号和当前环境状态选择下一个动作,选择的原则是让正强化(奖励)的概率加大。选择的动作不仅影响立即强化值,也影响下一时刻的状态和最终的强化值。
与监督学习不同的是,教师信号来自于环境不是我们提供的,自能提要通过自身的经历区学习,通过这种方式,智能体再行动被评价的化境中学习,改进行动方案来适应环境。
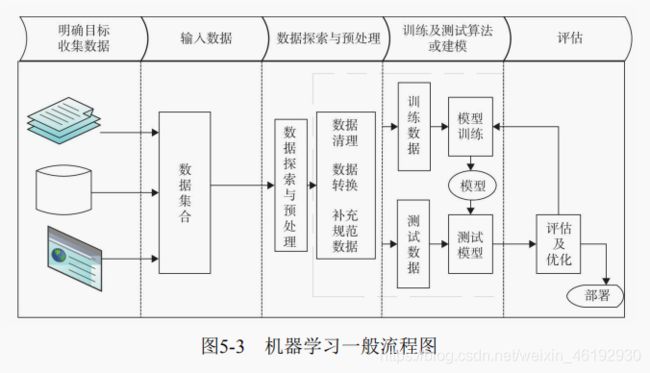
机器学习的一般流程
以前写的感觉更具体
过拟合和欠拟合
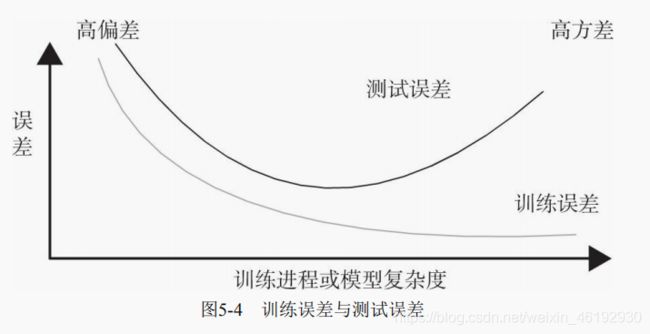
随之训练迭代次数的增加或不断优化,训练精度或损失值改善但测试精度或损失值不降反升。这就优化过头了,将训练数据种的一些无关甚至错误数据也学习了。解决过拟合的方法统称为正则化
权重正则化
显式的减少测试误差的策略就是正则化。减少泛化误差,通过正则化使参数变小甚至趋于原点。简单来说就是降低模型的复杂度,对于高次多项式就可以降低系数。
损失函数:

正则化:让 θ3 θ4 接近零
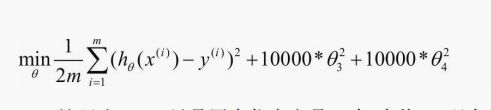

正则化一般分为 L0 L1 L2 L∞ 。
L2正则化就是权重衰减,torch.optim 里的优化器,如 SGD, Adiadelta,Adam,Adagrad RMSprop 等。都有一个自带的参数,weight_decay,用于指定权值衰减率,就相当于下面的 λ。
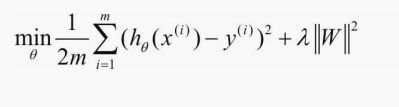
Dropout 正则化
一种针对神经啊网络模型的正则化。做法就是再训练过程中按一定比例(比例参数设置)随机忽略或屏蔽一些神经元,神经元被随机抛弃,也就是说他们再正向传播过程种对于下游神经元的贡献效果暂时消失,反向传播时该神经元也不会由任何权重的更新。所以,传播过程种Dropout 会产生和 L2 范数收缩权重相同的效果。
随着神经网络模型的不断学习,神经元的权值会与整个网络的上下文相匹配。神经元的权重针对某些特征进行优化,进而产生一些特殊变换,周围的神经元则会依赖于这种特殊化,但如果过于特殊化,模型会因为对训练数据的过拟合而变得脆弱,神经元再训练过程种的这种依赖于上下文的现象被称为复杂的协同效用(Complex Co-Adaptaions)
加入了Drpuout 后,输入的特征都有可能随机清除,所以该神经元不会再特别依赖于任何一个输入特征,也就是说不给给任何一个i输入设置太大的权重,由于网络模型对神经元特定的权重不那么敏感,这反过来由提升了模型的泛化能力,不容易对训练数据过拟合。
Dropout训练的集成包括所有从基础网络除去非输出单元形成子网络
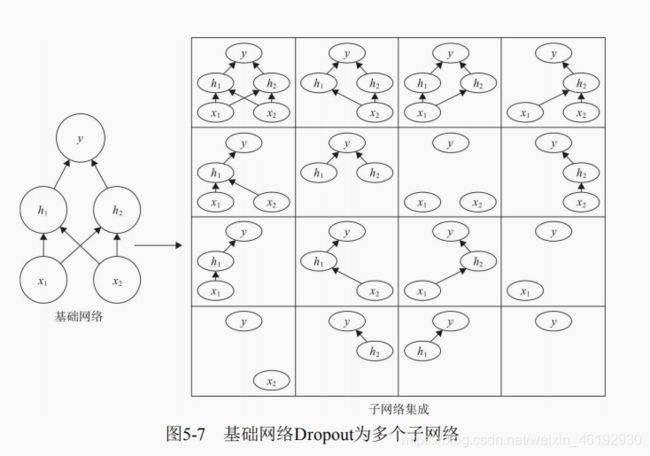
Dropout 训练所有去除非输出单元构成的子网络,这样就有16 个子网络,当层很宽时,丢弃所有从输入到输出的可能路径的概率很小,就不会像这个一样很多没有输入单元,或没有输入连接到输出的路径。至于删除单元的做法,就是乘零啦。
Dropout在训练阶段和测试阶段是不同的,一般在训练中使用,测试时不使用。不过在测试时,为了平衡(因训练时舍弃了部分节点或输出),一 般将输出按Dropout Rate比例缩小。
使用原则:
- 通常丢弃率再 20% - 50% ,比例太低没有效果,太高就可能导致欠拟合。
- 再大的网络上应用,再大的网络种更有可能得到效果的提升,模型有更多机会学习到多种独立的特种。
- 再输入层和隐藏层都使用Dropout ,神经元较小的层会设置keep_prob为接近1 的数,神经元较大设置0.5或更小
- 增加学习速率和冲量,将学习速率扩大10-100 倍,冲量值调高 0.9-0.99
- 限制网络模型的权重。大的学习速率往往会导致大的权重值。对网络的权重值做最大范数的正则化,可以提升模型的性能。
批量正则化
解决梯度消失问题的,就是 BN 批量归一化,还可以让调试超参数变得更加简单,提高训练模型效率的同时还可以让网络模型更加健壮。

这个 γ和β 是反向传播额外学习的参数,BN 是对隐藏层的标准化处理,与输入的标准化处理是有区别的,标准化输入是让输入的均值为0,方差为1。BN 是让个隐藏层输入的均值和方差为任意值(从激活函数的角度来看,如果各隐藏层的输入均值靠近0,即处于激活函数的线性区域,这样不利于训练好的非线性神经网络。
(5-7)就是中的两个额外参数代表缩放和平移的参数向量,离开线性区域,而且还可以通过简单的变换再回到原来的x 。BN 一般作用在非线性映射之前,再每一个全连接和激励函数之间。再神经网络训练出现收敛速度很慢,或梯度爆炸等无法训练的情况下可以使用BN 来解决。加入BN 可以加速训练速度,提高模型精度,提高训练模型的效率。
- 可以选择较大的初始学习率,让训练速度提升,之前还需要慢慢的调整学习率,现在就可以直接采用很大的学习率,然而学习率的衰减速率很快,因为这个算法具有快速训练收敛的特性。
- 采用了BN 后就可以不用选择 Dropout, L2 正则项的参数,可以移除,或选择更小的约束参数,因为BN 可以提高网络泛化能力的特性。
- 不需要使用局部相应归一化
- 可以将训练数据彻底打乱
比较一下两种的效果
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
boston = load_boston() # 波士顿房价的数据集
X,y = (boston.data, boston.target)
dim = X.shape[1]
# 分割训练集和测试集 20% 测试
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
num_train = X_train.shape[0]
#对训练数据进行标准化
mean=X_train.mean(axis=0)
std=X_train.std(axis=0)
X_train-=mean
X_train/=std
X_test-=mean
X_test/=std
train_data=torch.from_numpy(X_train)
dtype = torch.FloatTensor
train_data.type(dtype)
# 实例化模型
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
train_data=torch.from_numpy(X_train).float()
train_target=torch.from_numpy(y_train).float()
test_data=torch.from_numpy(X_test).float()
test_target=torch.from_numpy(y_test).float()
print(train_data.shape,test_data.shape)
# 四种网络
net1_overfitting = torch.nn.Sequential(
torch.nn.Linear(13, 16),
torch.nn.ReLU(),
torch.nn.Linear(16, 32), # 三层网络
torch.nn.ReLU(),
torch.nn.Linear(32, 1),
)
net1_bn = torch.nn.Sequential(
torch.nn.Linear(13, 16),
nn.BatchNorm1d(num_features=16), # 这个加上了批量归一化
torch.nn.ReLU(),
torch.nn.Linear(16, 32),
nn.BatchNorm1d(num_features=32),
torch.nn.ReLU(),
torch.nn.Linear(32, 1),
)
net2_bn = torch.nn.Sequential(
torch.nn.Linear(13, 8),
nn.BatchNorm1d(num_features=8), # 中间神经元个数少了
torch.nn.ReLU(),
torch.nn.Linear(8, 4),
nn.BatchNorm1d(num_features=4),
torch.nn.ReLU(),
torch.nn.Linear(4, 1),
)
net1_dropped = torch.nn.Sequential(
torch.nn.Linear(13, 16),
torch.nn.Dropout(0.5), # 丢去一半的神经元
torch.nn.ReLU(),
torch.nn.Linear(16, 32),
torch.nn.Dropout(0.5), # drop 50% of the neuron
torch.nn.ReLU(),
torch.nn.Linear(32, 1),
)
loss_func = torch.nn.MSELoss()
optimizer_ofit = torch.optim.Adam(net1_overfitting.parameters(), lr=0.01)
optimizer_drop = torch.optim.Adam(net1_dropped.parameters(), lr=0.01)
optimizer_bn = torch.optim.Adam(net1_bn.parameters(), lr=0.01)
optimizer_bn2 = torch.optim.Adam(net2_bn.parameters(),lr=0.01)
from tensorboardX import SummaryWriter
writer = SummaryWriter(log_dir='logs')
for epoch in range(200):
net1_overfitting.train()
net1_dropped.train() # 训练
net1_bn.train()
net2_bn.train()
pred_ofit = net1_overfitting(train_data).squeeze() # 进行预测
pred_drop = net1_dropped(train_data).squeeze()
pred_nb = net1_bn(train_data).squeeze()
pred_nb2 = net2_bn(train_data).squeeze()
loss_ofit = loss_func(pred_ofit, train_target)
loss_drop = loss_func(pred_drop, train_target)
loss_nb = loss_func(pred_nb, train_target) # 计算损失
loss_nb2 = loss_func(pred_nb2, train_target)
optimizer_ofit.zero_grad()
optimizer_drop.zero_grad() # 梯度清零
optimizer_bn.zero_grad()
optimizer_bn2.zero_grad()
loss_ofit.backward() # 反向
loss_drop.backward()
loss_nb.backward()
loss_nb2.backward()
optimizer_ofit.step() # 更新参数
optimizer_drop.step()
optimizer_bn.step()
optimizer_bn2.step()
# 保存loss的数据与epoch数值
# writer.add_scalar('train_loss', loss_ofit, t)
writer.add_scalars('train_group_loss', {'train_ofit_loss': loss_ofit.item(),
'train_nb_loss': loss_nb.item(),
'train_drop_loss': loss_drop.item(),
'train_nb2_loss':loss_nb2.item()}, epoch)
# change to eval mode in order to fix drop out effect
net1_overfitting.eval()
net1_dropped.eval() # 不在求梯度
net1_bn.eval()
net2_bn.eval()
test_pred_orig = net1_overfitting(test_data).squeeze() # 使用测试集
test_pred_drop = net1_dropped(test_data).squeeze()
test_pred_nb = net1_bn(test_data).squeeze()
test_pred_nb2 = net2_bn(test_data).squeeze()
orig_loss = loss_func(test_pred_orig, test_target)
drop_loss = loss_func(test_pred_drop, test_target)
nb_loss = loss_func(test_pred_nb, test_target)
nb_loss2 = loss_func(test_pred_nb2, test_target)
# writer.add_scalars('test_nb_loss',{'orig_loss':orig_loss.item(),'nb_loss':nb_loss.item()}, epoch)
writer.add_scalars('test_group_loss',
{'droploss': drop_loss.item(), 'origloss': orig_loss.item(), 'nb_loss': nb_loss.item(),'np_loss2':nb_loss2.item()}, epoch)

??? 这河里吗。。。感觉加不加 dropout 好像没啥区别啊。。。为啥人家的效果就那么明显呢。。。不够BN 的作用还是明显的(用了对数坐标轴后,相差也不算太大的)
权重初始化
深度学习的算法一般采用迭代方法,而且参数多层数也多,所以不行机器学习一样需要初始化的参数不多。
初始化可以决定算法是否收敛,初始值过大可能导致传播过程中出现爆炸值,过小导致丢失信息。适当的初始化可以加快收敛速度,影响模型收敛局部最小值还是全局最小值。。
一般采用正太分布或均匀分布的初始值。继承自nn.Module 的模块参数都采用了较合理的初始化策略,一般情况下使用默认的初始化策略就行。如果要修改可以使用 nn.init 模块,提供了常用的初始化策略,比如 xavier, kaiming 等。使用这些初始化策略有利于激活值得分布呈现更有过度或更贴近正态分布。。xavier 适合S 型得权重初始化,kaiming 适合ReLU 类得权重初始化