归并排序算法(java实现)
基本思想
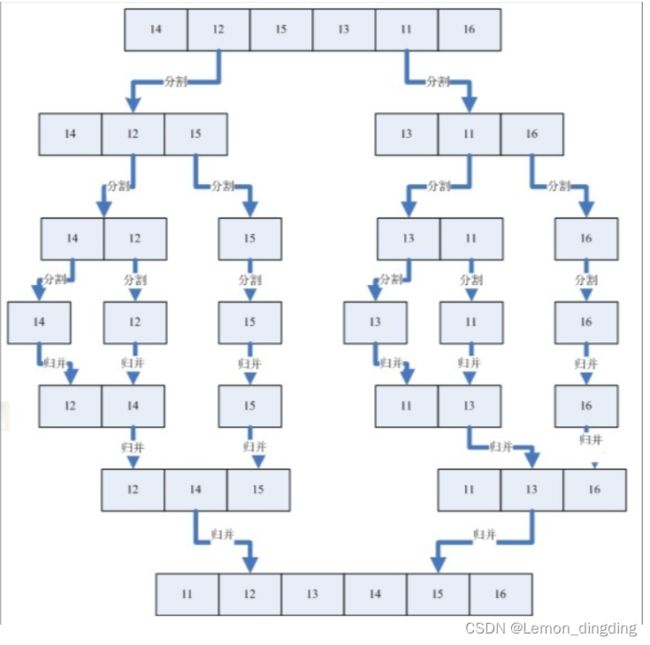
归并排序是由递归实现的,主要是分而治之的思想,也就是通过将问题分解成多个容易求解的局部性小问题来解开原本的问题的技巧。
归并排序在合并两个已排序数组时,如果遇到了相同的元素,只要保证前半部分数组优先于后半部分数组, 相同元素的顺序就不会颠倒。所以归并排序属于稳定的排序算法。
每次分别排左半边和右半边,不断递归调用自己,直到只有一个元素递归结束,开始回溯,调用 merge 函数,合并两个有序序列,再合并的时候每次给末尾追上一个最大 int 这样就不怕最后一位的数字不会被排序。
归并排序的效率是比较高的,设数列长为N,将数列分开成小数列一共要logN步,每步都是一个合并有序数列的过程,时间复杂度可以记为O(N),故一共为O(N log N)。因为归并排序每次都是在相邻的数据中进行操作,所以归并排序在O(N*logN)的几种排序方法(快速排序,归并排序,希尔排序,堆排序)也是效率比较高的。
排序过程
算法流程:
1、将一个数组拆分为两个,从中间点拆开,通过递归操作来实现一层一层拆分。
2、从左右数组中选择小的元素放入到临时空间,并移动下标到下一位置。
3、重复步骤2直到某一下标达到尾部。
4、将另一序列剩下的所有元素依次放入临时空间。
5、将临时空间的数据依次放入原数据数组。
基础代码
package Sort;
//针对 一个数组 左右两部分已经排好序
public class 归并排序基础 {
public static void main(String[] args) {
int[] arr = {1,4,7,8,3,6,9};
merge(arr);
}
// 把数组arr = {1,4,7,8,3,6,9} 分成两部分 分别为1,4,7,8 和 3,6,9
static void merge(int[] arr) {
int mid = arr.length / 2;
int[] temp = new int[arr.length];
int i = 0; //i是数组arr前部分的第一位
int j = mid+1; //j是数组arr后部分的第一位
int k = 0; //k是 新数组temp的第一位
//当 arr数组两边都还有数 时
while (i <= mid && j < arr.length) {
if (arr[i] <= arr[j]) {
temp[k] = arr[i];
i++;
k++;
} else {
temp[k] = arr[j];
j++;
k++;
}
}
//将右边剩余的归并
while (i <= mid) {
temp[k++] = arr[i++];
}
//将左边剩余的归并
while (j < arr.length) {
temp[k++] = arr[j++];
}
print(temp);
}
//排序
static void swap(int[] arr,int i,int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
//打印
static void print(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}
加入归并的代码
package Sort;
public class 归并排序递归 {
public static void main(String[] args) {
// int[] arr = {1,4,7,8,3,6,9};
int[] arr = {3,0,6,4,1,3,7,8,5,9};
sort(arr,0,arr.length-1);
print(arr);
}
public static void sort(int[] arr,int left,int right) {
if (left == right) {
return;
}
//分成两半
int mid = left +(right-left)/2;
//左边排序
sort(arr, left, mid);
//右边排序
sort(arr, mid +1, right);
merge(arr, left, mid+1, right);
}
//leftPtr 指数组最左边
//rightPtr 指数组中间
//rightBound 数组最右边
static void merge(int[] arr,int leftPtr,int rightPtr,int rightBound) {
int mid = rightPtr - 1;
int[] temp = new int[rightBound - leftPtr + 1];
int i = leftPtr;
int j = rightPtr;
int k = 0;
while (i <= mid && j <= rightBound) {
if (arr[i] <= arr[j]) {
temp[k] = arr[i];
i++;
k++;
} else {
temp[k] = arr[j];
j++;
k++;
}
}
// 将右边剩余的归并
while (i <= mid) {
temp[k++] = arr[i++];
}
//将左边剩余的归并
while (j <= rightBound) {
temp[k++] = arr[j++];
}
for(int m = 0; m < temp.length;m++) arr[leftPtr+m] = temp[m];
}
//排序
static void swap(int[] arr,int i,int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
//打印
static void print(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}