【论文阅读】Forecasting at scale
Forecasting at scale
- 一、前言
- 二、背景
-
- 1、数据集
- 2、现有模型
- 三、prophet 模型
-
- 1、模型概述
- 2、趋势部分
-
- 2.1、非线性模型
- 2.2 线性模型
- 2.3 自动变点选择
- 2.4 趋势预测的不确定性
- 3、周期项
- 4、节假日事件项
- 5、模型拟合
- 6、分析闭环建模
- 三、预测自动评估
-
- 1、使用基线预测
- 2、模型预测精度
- 3、模拟历史预测
- 4、 识别大的预测误差
- 四、结束语
一、前言
该文章是fbprophet 提出时对应的官方论文,同时fbprophet官方文档可以进该网站,了解fbprophet的实际使用与参数配置等方法。该论文中具体包括了fbprophet的原理,公式,特点,以及构建该模型的一些出发点,动机;数据预测与基线模型的对比,以及闭环时序预测的理念展示。阅读该文章对于初次接触fbprophet模型的人来说可以较好的对fbprophet模型有一个全面的了解。
二、背景
1、数据集
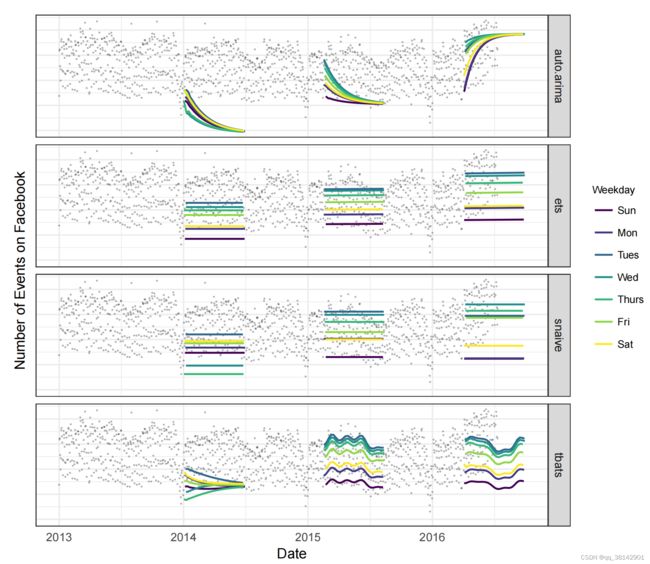
数据取自facebook的事件数在时间上的统计数据,其数据如下图2,可以发现数据集存在明显的周效应,年效应,异常值,在每年的年底会有一个短暂的低谷点,根据业务知识可以知道是由于感恩节与圣诞节,以及在2016年后出现了明显的趋势变化,这是Facebook一些新的产品发布所引起。接下来我们用我们常用的时序序列预测模型进行拟合,看这些模型们的表现。

2、现有模型
ARIMA自回归综合移动平均模型,可以发现其在凹点处的误差非常大,而且没有拟合到周期性的效应;ets(由误差项,趋势项与季节项组成,也叫指数平滑模型)与snaive(季节朴素预测法),可以看到这两个模型拟合到了周效应,但是对长期效应拟合失败;tbats模型(用指数平滑的方式来对复杂季节因素进行建模)捕捉到了周效应与年效应,但是这些均对年自适应性的节假日拟合很差。由现有模型的原理与表现,提出了作者提出新模型的动机是希望建立一个模块化的,拥有直观理解的参数且可以被拥有业务知识的分析师进行直观的调整,这个模型可以满足对趋势的调整,周期效应的捕捉,节假日的配置,这样大大简化了对预测人员的要求(现有模型大部分调整需要具有统计知识),提高了观测人员的工作效率(直观的参数与直观的可视化功能,以及闭环的建模设计)。
三、prophet 模型
1、模型概述
prophet模型由趋势项,周期项,节假日事件项与误差项组成,g(t)是趋势函数,可以设置不同的可变趋势;s(t)是周期项,可以设置多个周期;h(t)节假日事件项,可以设置多个节假日事件项;这里面误差项假设其符合正态分布。该模型拟合速度快,无需规律的次序分布即无需对缺失值进行特别处理。同时其模块组合的方式,对回归较了解的分析师还可以对现有模型进行扩展,添加新的组成成分。
2、趋势部分
这块注意有两种趋势选择:饱和生长模型(也叫罗辑回归logistic,如生态系统的生长模式类有天花板的存在),分段式线性模型。
2.1、非线性模型
整体公式如(3),
C(t)为容量阈值(天花板),这里可以根据不同的业务知识与一些额外的数据去得到一个变化的C(如随着新产品的上市,其客户容量扩大一倍等情况);
k为增长率,通常是一个常数,在实际场景中它可能会随着时间的变化发生改变(如促销,用户量的增长),因此增加了变点来改变增长率,假设有S个变点在时间 s j s_j sj上,其中j=1,…,S;那么定义调整率向量为 δ \delta δ, δ j \delta_j δj为时间 s j s_j sj上的变化率;则t> s j s_j sj后的增长率等于k加上前面变点的全部调整率( k + ∑ j : t > s j δ j k+\sum_{\substack{j:t>s_j}}\delta_j k+∑j:t>sjδj),为方便表示,引入a(t),其构造如下
a ( t ) = { 1 if t ⩾ s j 0 if 其它 a(t) = \begin{cases} 1 &\text{if } t\geqslant s_j \\ 0 &\text{if } 其它 \end{cases} a(t)={10if t⩾sjif 其它
m是调整变点处的连接,其 γ \gamma γ计算如下

其中变点的向量 δ \delta δ,可以自动根据历史数据算出,得到先验分布 δ j \delta_j δj~Laplace(0, τ \tau τ),这里面的参数 τ \tau τ可以直接控制模型趋势改变的灵活性,当参数 τ \tau τ趋于0时,趋势函数变为不分段的趋势函数。
在实际使用中变点除了可以让模型自动选择,还可以手动进行设置。

由上面的公式可以看到趋势函数的个性化程度高,主要表现在可变的限制设置,与灵活性可调的趋势变化上。
同时在个性化时要注意其设定均是根据历史数据得到,也就意味着趋势改变的频率与大小与历史上的表现强相关,理论上参数 τ \tau τ增加,趋势项越灵活,训练误差越小,但是这样也会造成模型过拟合的风险增大。
2.2 线性模型
线性趋势,容易根据非线性模型得到,同样可以设置变点,变化灵活性参数。

2.3 自动变点选择
变点数可以根据专家的建议进行明确的指定,也可以通过先验分布 δ j \delta_j δj~Laplace(0, τ \tau τ)根据趋势模型自动进行选择;其中参数 τ \tau τ控制了模型变点的改变率的灵活性,注意的是,调整率 δ \delta δ的稀疏先验性不影响原始生长率k,因此 τ \tau τ趋于零时,模型拟合为标准的非分段逻辑回归或者线性生长趋势。
2.4 趋势预测的不确定性
如果模型直接根据历史推断未来,趋势将有一个常数率。在本文模型中,未来趋势根据历史变点其对应的变化率分布仿真或者最大似然得出未来的变化率,未来变点由历史里匹配的变点的平均频率进行随机采样得到。以上对未来趋势的预测基于以下假设:未来趋势会以历史里同样的平均频率与幅度的变化率发生,因此未来的趋势预测的强烈依赖历史,其覆盖的变化区间(仿真或者最大似然得到置信区间)不一定完全覆盖住未来实际情况; τ \tau τ越大,其对历史的拟合越贴合,训练误差越小,同时过拟合的风险越大。
3、周期项
周期采用傅立叶函数实现,这个比较好理解,关键是里面N的选择,与参数的估计(放到后面的模型拟合出实现),其中N越大意味着周期性的模式变化越快,同样的其过拟合的风险也会增大;在本文中,作者建议年效应N选10,周效应N选3;其它周期性效应可以用AIC进行选择。

4、节假日事件项
采用节假日名称,对应日期(事件影响就对应日期这一天);或者节假日名称,开始日期,与涉及区间;通过产生一个回归矩阵,类似周期性起作用,其公式如下:

5、模型拟合
将周期特征与事件特征与观测值组合起来为X,变点指示器a(t)表示为矩阵A,则一个完整的模型如下图,其中k,m为上方提到的趋势增长率,变点处连接参数,epsilon即 ϵ \epsilon ϵ为随机误差,delta 为变点对应的分布,beta为周期性的先验分布。采用L-FBFGS 优化算法进行最大后验估计进行模型拟合,可分解模型的一个重要优势在于可以分开来看每一个组成的预测情况,有利于我们直观的洞察到模型上问题,从而进行调整,得到最终预测。下面模型中的参数 τ \tau τ, σ \sigma σ控制着模型变点部分与周期性部分的正则力度,是防止模型过拟合的重要参数。通常模型的默认值能适用大部分场景,当需要调整时,可以采用交叉验证进行参数调优。
6、分析闭环建模
该模型无需任何对统计基础的了解,即可应用分析者的业务知识与专业能力进行模型调整。对容量上限参数,变点,节假日与周期性,平滑参数,可结合自己的业务与专业知识与优秀的绘图工具即可进行调整,从而改变模型。对趋势,周期性,节假日成分的可视化,可以很快的对模型拟合情况进行直观的判断,有利于使用者快递调整检验模型,提升使用者的建模效率。
预测通常分为概率型预测与决策型预测,前者的优势在于容易适用更多场景,后者优势在于对场景内发生变化时更具代表性即泛化性能强,当然这要求分析者进行更多的投入。本文模型试图将两种类型的优势组合起来,因此设计出了类似转换可视化建模的方式,既给出很多直观的参数与选项,同时也保留了自动进行统计预测的能力。当然分析闭环的建模方式在很大程度上依赖于对预测结果的自动评估与优秀的可视化工具上,在这一块本文团队也将不断完善最新预测上的评估与分析。
三、预测自动评估
1、使用基线预测
与基线预测对比是出于在实际应用中基线预测产生的是一个合理的预测,最简单的基线预测如最近的值或者样本均值。
2、模型预测精度
预测通常会定一个水平基线H(外推预测多长),在本文作者的项目中通常是30,90,180,365天作为水平基线。衡量模型的精度采用下方公式进行,h表示预测的第几天,T表示历史数据的最新日期,d()为计算预测值与实际值的距离函数,在算法中,距离函数的选择也是一个需要进行探讨的问题,本文作者采用的是平均绝对百分比误差MAPE。
![]()
在衡量模型精度中通常有两种方式,一个是根据模型拟合公式,去估计误差项的方差,但是这个方法是建立在正确搭建模型的基础上,显然这个在实际应用中无法实现,因此我们在实际应用中均采用第二种方式,即采用对历史数据的预测,通过上方公式进行计算,来对模型精度进行评估。
3、模拟历史预测
采用历史预测的时候,有两个问题要注意,一是决定进行多少历史预测合适,选择过多的话计算量大,且邻天之间的误差与信息通常是很相似的;选择过少的话又无法很好的评估模型精度从而进行选择,文中作者提出,在直观感受下,给定水平基线H,通常进行H/2的历史预测进行精度评估。二是预测方法在更多数据下可能更坏,也可能更好,在模型错误拟合与者过拟合下,一个更长的历史可能会导致更糟糕的预测。因此在进行模拟历史预测时,可以选用不同的水平基线H进行,以及改变不同的预测起点进行,可以比较全面的对模型精度进行评估。
4、 识别大的预测误差
基于历史预测,有以下几种方法去识别:
– 当与基线相比预测误差大时,很有可能是模型搭建有误,此时可以根据需要调整模型的趋势或者周期性等。
– 当在所有方法中均误差大时,此时可能是数据中有异常值,分析者可以进行异常数据识别,并去除它。
– 误差只只某一段历史预测开始突然增大,这有可能是数据突然发生了大的变化,此时可以添加变点,或者对不同阶段进行单独建模进行解决。
当然这些方法不总是正确的,不过本文作者遇到的问题大部分能通过调整变点与异常点剔除进行解决,一旦在回测与可视化中发现预测的波动,这些问题可以快速的被识别出来。
四、结束语
到这里,这篇论文的核心内容就结束了,此文只做个人学习的笔记与理解记录,若有理解错误的地方,欢迎大家指正。