统计学基础——常用的概率分布(二项分布、泊松分布、指数分布、正态分布)
变量类型:
- 连续型变量 如:指数分布、正态分布
- 离散型变量 如:二项分布、泊松分布
三者之间的关系
![]()
二项分布(Binomial distribution)
二项分布(Binomial distribution)是n重伯努利试验成功次数的离散概率分布,记作。伯努利试验是只有两种可能结果的单次随机试验。
伯努利试验都可以表达为“是或否”的问题。例如,抛一次硬币是正面向上吗?刚出生的小孩是个女孩吗?等等
- 如果试验E是一个伯努利试验,将E独立重复地进行n次,则称这一串重复的独立试验为n重伯努利试验。
- 进行一次伯努利试验,成功(X=1)概率为p(0<=p<=1),失败(X=0)概率为1-p,则称随机变量X服从伯努利分布。伯努利分布是离散型概率分布,伯努利分布(Bernoulli distribution)又名两点分布或0-1分布。
二项分布的三个特点:
- 每次实验结果,只能是两个互斥的结果之一。
- 各次实验独立,各次的实验结果互不影响。。
- 相同的实验条件下,每次实验中事件A的发生具有相同的概率
 。
。
二项分布的概率函数![]() 可用公式
可用公式
其中,![]()
对于任何二项分布,总有
例1.如果某地钩虫感染率为13%,随机观察当地150人,其中恰好有10人感染钩虫的概率有多大?
分析:
(1)钩虫感染只有两个互斥的结果,即感染与非感染;
(2)每个人被钩虫感染的概率相同;
(3)人与人之间钩虫感染可假设为相互独立的,所以感染钩虫的人数 X 可认为服从 n = 150,π = 0.13的二项分布。
二项分布的特征
- 是二项分布的两个参数,所以二项分布的形状取决于(阳性率)。
- 当
 =0.5时分布对称,近似对称分布。
=0.5时分布对称,近似对称分布。 - 当
 ≠0.5时,分布呈偏态,特别是
≠0.5时,分布呈偏态,特别是  较小时,
较小时, 偏离0.5越远,分布的对称性越差,但只要不接近1和0时,随着
偏离0.5越远,分布的对称性越差,但只要不接近1和0时,随着 的增大,分布逐渐逼近正态。
的增大,分布逐渐逼近正态。 - 当
 或 不太小,而
或 不太小,而  足够大,通常 和 均大于或等于5,我们常用正态近似的原理来处理二项分布的问题。
足够大,通常 和 均大于或等于5,我们常用正态近似的原理来处理二项分布的问题。
二项分布的正态近似
- 根据中心极限定理,在
 较大,与 均大于或等于5时,二项分布接近与正态分布。
较大,与 均大于或等于5时,二项分布接近与正态分布。 - 当
 无穷大时,二项分布B()的极限分布是总体均数为,总体标准差为的正态分布,此时可用该正态分布进行估计。
无穷大时,二项分布B()的极限分布是总体均数为,总体标准差为的正态分布,此时可用该正态分布进行估计。
二项分布的均数和标准差
对于任何一个二项分布,如果每次试验出现“阳性” 结果的概率均为![]() ,则在
,则在 ![]() 次独立重复实验中:
次独立重复实验中:
1、出现 X 次阳性结果
总体均数(出现阳性结果的次数X的均值):
标准差(出现阳性结果的次数X的标准差):
2、阳性结果的频率记做为
![]() 的总体均数(出现阳性结果频率
的总体均数(出现阳性结果频率![]() 的均值):
的均值):
标准差(出现阳性结果频率![]() 的标准差):
的标准差):
是频率P的标准误,反映阳性频率的抽样误差的大小。
泊松分布(Poisson distribution)
泊松分布是二项分布在阳性率特别小时的一种情形,用于描述单位时间、空间、面积等的罕见事件发生次数的概率分布,如:
- 每毫升水中的大肠杆菌数
- 单位时间(如1分钟)内放射性质点数
- 每1000个新生儿中某出生缺陷、多胞胎、染色体异常等事件出现的例数
泊松分布的三个特点:
泊松分布是二项分布当中的一种特殊情况,则泊松分布也遵循二项分布的三个特点:
- 观察结果相互独立
- 每次试验只有两个结果
- 发生的概率
 不变
不变
如,人群中传染性疾病首例出现后便成为传染源,会增加后续病例出现的概率,因此病例数的分布不能看作是Poisson分布。
又如,污染的牛奶中细菌成集落存在,单位容量牛奶中细菌数不能认为服从Poisson分布。
泊松分布分布一般记作![]() ,其概率函数为:
,其概率函数为:
![]()
式中,![]() 为Poisson分布的总体均数(
为Poisson分布的总体均数(![]() 表示概率);
表示概率);![]() 为观察单位内某稀有事件的发生次数;
为观察单位内某稀有事件的发生次数;![]() 为自然对数的底,为常数,约等于2.71828,自然对数的底数e是由一个重要极限给出的:当
为自然对数的底,为常数,约等于2.71828,自然对数的底数e是由一个重要极限给出的:当![]() 趋于无限时,
趋于无限时,![]() 。
。
泊松定理(泊松分布是二项分布当中的一种特殊情况)
设随机变量服从二项分布,即。其中,是与![]() 有关的数,且设是常数,则有,
有关的数,且设是常数,则有,
证明:依题设有,代入中,有
对于固定的![]() ,有
,有
(根据![]() )
)
所以,
可见,二项分布的极限分布是泊松分布,当n很大,![]() 很小时,可用近似代替,一般时,可采用上次近似公式代替。
很小时,可用近似代替,一般时,可采用上次近似公式代替。
泊松分布的特征
- 随着
 的增大,Poisson分布逐渐趋于对称分布。
的增大,Poisson分布逐渐趋于对称分布。 - 当
 >20时,Poisson分布可视为近似正态分布。
>20时,Poisson分布可视为近似正态分布。
下图表示出了![]() 对泊松分布的影响,
对泊松分布的影响,![]() 表示泊松分布的均值。当
表示泊松分布的均值。当![]() 变大时,不仅整个分布模式向右移动,数据也更加分散,方差随之变大。
变大时,不仅整个分布模式向右移动,数据也更加分散,方差随之变大。
![]()
泊松分布的特性
- 总体均数与总体方差相等:均为
 。
。 - 可加性:从总体均数分别为
 1 和
1 和 2 的两个Poisson分布总体中各自随机抽出一份样本,其中稀有事件的发生次数分别为
2 的两个Poisson分布总体中各自随机抽出一份样本,其中稀有事件的发生次数分别为 和
和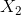 ,则合计发生数也服从Poisson分布,总体均数为
,则合计发生数也服从Poisson分布,总体均数为 1 +
1 + 2 。
2 。
可加性的运用:分5次,每次都是监测5毫升的水样,得到的![]() 都比20小,但是5次
都比20小,但是5次![]() 相加的之后形成的
相加的之后形成的![]() 比20大的话,我们就可以10毫升水样当中的细菌数的分布用正态近似法了
比20大的话,我们就可以10毫升水样当中的细菌数的分布用正态近似法了
例:某放射性物质半小时内发出的脉冲数服从Poisson分布,平均为 360个,试估计该放射性物质半小时内发出的脉冲数大于400个的概率。
其中,0.5表示连续型校正,表示处理离散型变量,应用到连续型的正态分布的时候,效果更佳的一种修正。
注意:泊松分布不具备可乘性。
指数分布
设随机变量X的分布密度函数为
![]()
其中![]() 为常数,我们称
为常数,我们称![]() 服从参数为
服从参数为![]() 的指数分布,记作,其相应的分布函数为
的指数分布,记作,其相应的分布函数为
![]() 和
和![]() 的图形见下图。
的图形见下图。
![]()
指数分布的特性
- 总体均数,总体方差。
指数分布通常用作各种“寿命”的分布。例如,无线电元件的寿命,动物的寿命等,另外电话问题的通话时间、随机服务系统中的服务时间等都可以认为服从指数分布,因此,它在排队论和可靠性理论等领域中有广泛的应用。
例、某电子元件的使用寿命X是一个连续型随机变量,其概率密度为
(1)确定常数k
(2)求寿命超过100小时的概率
(3)已知该元件已经正常使用200小时,求它至少还能正常使用100小时的概率。
解:
(1)由概率密度函数性质2知
,得。
(2)寿命超过100小时的概率为
(3)条件概率
由(2),(3)可知,该元件寿命超过100小时的概率等于已使用200小时的条件下至少还能使用100小时的概率,这个性质称为指数分布的“无记忆性”。
若随机变量X对任意的都有,则称X的分布具有无记忆性。
因此,指数分布具有无记忆性,若某元件或动物的寿命服从指数分布,则上式表明,如果已知寿命长于s年,则再“活”t年的概率与s无关,即对过去的s时间没有记忆,也就是说只要在某时刻s仍“活”着,它的剩余寿命的分布和原来的寿命分布相同,所以人们也戏称指数分布是“永远年轻的”。
正态分布(Normal distribution)
正态分布的概率密度函数(即纵向的曲线高度)
![]() ,
,![]()
![]() 规定了曲线的形状,
规定了曲线的形状,![]() 反应了其在横轴上的位置不同。
反应了其在横轴上的位置不同。
正态分布的特征
- 关于
 对称,即正态分布以均数为中心,左右对称。
对称,即正态分布以均数为中心,左右对称。 - 在
 处取得概率密度函数的最大值,在处有拐点,表现为 钟形曲线。即正态曲线在横轴上方均数处最高。
处取得概率密度函数的最大值,在处有拐点,表现为 钟形曲线。即正态曲线在横轴上方均数处最高。 - 正态分布有两个参数,即均数
 和标准差
和标准差 。
。 是位置参数,
是位置参数, 是变异度参数(形状参数)。常用
是变异度参数(形状参数)。常用 表示均数为
表示均数为 ,标准差为
,标准差为 的正态分布;用表示标准正态分布。
的正态分布;用表示标准正态分布。 - 正态曲线下面积分布有一定规律。横轴上正态曲线下的面积等于1(也常写作100%)。
正态方程的积分式(概率分布函数):
概率分布函数即为正态概率密度曲线下的面积 。
![]() 为正态变量
为正态变量![]() 的累计分布函数,反映正态曲线下,横轴尺度自
的累计分布函数,反映正态曲线下,横轴尺度自![]() 到
到![]() 的面积,即下侧累计面积。
的面积,即下侧累计面积。
标准正态分布
均数为0,标准差为1的正态分布,这种正态分布称为标准正态分布。
对于任意一个服从正态分布![]() 的随机变量,可作如下的标准化变换,也称
的随机变量,可作如下的标准化变换,也称![]() (z-score)变换:
(z-score)变换:
其中,![]() ,标准正态分布的概率密度函数:
,标准正态分布的概率密度函数:
标准正态分布方程积分式(概率分布函数):
为标准正态变量![]() 的累计分布函数,反映标准正态曲线下,横轴尺度自
的累计分布函数,反映标准正态曲线下,横轴尺度自![]() 到
到![]() 的面积,即下侧累计面积,如下图所示。
的面积,即下侧累计面积,如下图所示。
![]()
标准正态分布表
用查表代替计算必须注意:
- 表中曲线下面积为
 到
到 的面积。
的面积。 - 当
 ,
, 和
和 已知时,先求出
已知时,先求出 值,
值,  ,再用Z值查表,得所求区间占总面积的比例。
,再用Z值查表,得所求区间占总面积的比例。 - 当
 和
和 未知时,要用样本均数
未知时,要用样本均数 和样本标准差
和样本标准差 来估计
来估计 值,。
值,。 - 曲线下对称于0的区间,面积相等。
- 曲线下横轴上的面积为1 (即100% )。
正态分布是一种对称分布,其对称轴为直线,即均数位置。
理论上:
- 范围内曲线下的面积占总面积的68.27%
- 范围内曲线下的面积占总面积的95%
- 范围内曲线下的面积占总面积的99%
实际上:
- 范围内曲线下的面积占总面积的68.27%
- 范围内曲线下的面积占总面积的95%
- 范围内曲线下的面积占总面积的99%
实际应用中,我们一般将1.96看似成2,2.58看似成3。
![]()
标准正态分布的![]() =0,
=0,![]() =1,则
=1,则
- 相当于区间(1,1)
- 相当于区间(1.96,1.96)
- 相当于区间(2.58,2.58)
- 区间(1,1)的面积:=1-2×0.1587=0.6826=68.26%
- 区间(1.96,1.96)的面积:=1-2×0.0250=0.9500=95.00%
- 区间(2.58,2.58)的面积:=1-2×0.0049=0.9902=99.02%
例: 已知某地1986年120名8岁男童身高均数 ,,估计(1)该地8岁男孩身高在130以上者占该地8岁男孩总数的百分比;(2)身高界于120~128者占该地8岁男孩总数的比例;(3)该地80%男孩身高集中在哪个范围?
(1)先做标准化转换:
根据标准正态分布的对称性
理论上该地8岁男孩身高在130 以上者占该地8岁男孩总数的7.21%。
(2)
(3)
查标准正态分布界值表,标准正态分布曲线下左侧面积为0.10所对应的
值为1.28,所以80%的8岁男孩身高值集中在区间内,即116.9~129.2。
正态分布的应用
制定参考值范围的步骤:
- 选择足够数量的正常人作为调查对象。
- 样本含量足够大。
- 确定取单侧还是取双侧正常值范围。
有些指标过高过低都是异常的,我们需要制定双侧的正常值范围
有些指标过低才是异常的,比如肺活量,我们只要制定单侧的正常值范围
- 选择适当的百分界限。
在实际操作当中,我们一般将正常人中的5%排除在外,计算95%参考值范围。
- 选择适当的计算方法。
![]()
正态近似法:适用于正态分布或近似正态分布的资料。
例1 某地调查120名健康女性血红蛋白,直方图显示,其分布近似于正态分布,得均数为117.4g/L,标准差为10.2g/L ,试估计该地正常女性血红蛋白的95%医学参考值范围。
分析:正常人的血红蛋白过高过低均为异常,要制定双侧正常值范围。
该指标的95%医学参考值范围为97.41~137.39(g/L)
百分位数法:适用于偏态分布资料。
例2 某年某市调查了200例正常成人血铅含量(μg/100g) 如下,试估计该市成人血铅含量的95%医学参考值范围。
![]()
分析:血铅的分布为偏峰分布,且血铅含量只以过高为异常,要用百分位数法制定单侧上限。