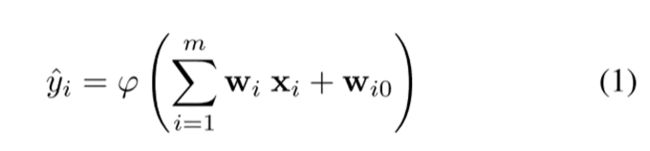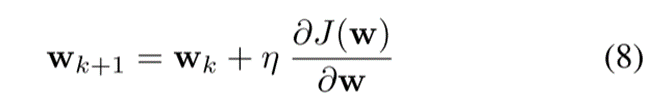2023/12/31周报

摘要

本周阅读了一篇关于时序预测在汇率中的应用的文章，作者混合使用多种非线性模型，还调整了自回归积分移动平均（ARIMA）和自回归分数积分移动平均（ARFIMA）模型，用多种误差指标分析结果，结果表明，混合神经网络模型优于其他方法来预测汇率。此外，还对self-attention等内容进行复习和代码实现。

Abstract

This week, an article about the application of time series forecasting in exchange rate is readed. The author uses a variety of nonlinear models, and also adjusts the autoregressive integral moving average (ARIMA) and autoregressive fractional integral moving average (ARFIMA) models. The results are analyzed with various error indicators. The results show that the hybrid neural network model is superior to other methods in forecasting exchange rate. In addition, the self-attention and other contents are reviewed and the code is implemented.

文献阅读

题目

时间序列预测中的深度学习技术：在汇率中的应用

引言

在特定的汇率下，预测金融序列在决策、投资组合配置、风险管理和衍生品定价问题中起着关键作用。近年来，机器学习模型由于其处理非线性关系的能力而被应用于时间序列预测。这项研究评估了神经网络模型，如MLP，LSTM，GRU和拟议的AE-BiGRU-Swish预测汇率序列。使用深度学习技术调整了这些模型的参数，比较了神经网络模型预测汇率序列的性能与传统的方法，如ARIMA和ARFIMA模型的时间范围为1，7，14，21和30天的提前预测。结果表明，混合神经网络模型优于其他方法来预测汇率。

本文中，作者提出了使用非线性模型，特别是非递归多层感知器神经网络，长短期记忆，门控递归单元网络和AutoEncoder双向门控递归单元多步提前（1，7，14，21和30天）预测汇率，试图验证这些模型是否可以捕捉汇率序列中的非线性关系。
为了评估非线性模型的性能，作者还调整了自回归积分移动平均（ARIMA）和自回归分数积分移动平均（ARFIMA）模型，并根据MAE，MAPE，MSE，RMSE，ACCURACY和CE等误差指标比较结果。

模型与方法

多层感知器神经网络MLP

MLP是静态的，模型输出表示如下：

其中，φ（·）是激活函数， ∑是输入的线性聚合函数，由权重W加权。
MLP训练需要确定通过误差反向传播算法（BP）获得的权重向量w。
BP算法基于误差校正规则，这意味着应用迭代的基于梯度的方法，该方法寻求最小化估计输出y和期望输出y。信息处理有两个步骤：向前和向后。前向步骤通过网络传播输入，生成输出（传播），后向步骤包括基于误差 计算成本函数的梯度，通过以下公式获得：

BP算法使用基于向下梯度的搜索技术：

最后用下式更新W：

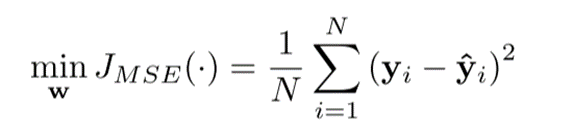
其中η ∈ [0，1]是学习率或自适应步长， ∇(·)是梯度算子。

LSTM

LSTM单元由输入信号Xi和输出yi-1反馈，LSTM单元在所有阶段共享相同的参数。

LSTM使用误差反向传播时间算法（BPTT）进行估计，该方法旨在最小化模型提供的输出与期望输出之间的成本函数：

BPTT计算成本函数关于向量w的导数：

使用以下公式更新W：

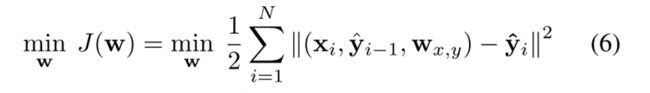
GRU

门控递归单元（GRU）是LSTM单元的简化版本，以相同的方式工作。
GRU是一个动态模型，它提供递归映射并存储先前状态的信息，以影响当前时刻的预测。GRU与其他网络的不同之处在于，它将细胞的整个状态暴露给网络中的其他单元，而LSTM细胞控制其内存内容的暴露。GRU单元有两个因子：更新因子zt，即遗忘门和输入门在单个门上的连接点，以及复位因子rt。

AE-BiGRU-Swish神经网络

本文提出混合模型AE-BiGRU-Swish，结合了监督和无监督学习。该模型与其他模型一起进行了跨不同时间范围（长达30天）的多步预测测试。自动编码器（AE）是一种利用无监督学习的神经网络模型。它由两个主要阶段组成：编码器和解码器。在编码器中，输入数据被转换为较低的维度，而解码器的目标是基于编码层提供的压缩表示来重新创建原始输入。在训练期间，目标是最大化原始输入数据的重建并最小化重建误差（等式9）。编码器（CODEC）包括两个连续的双向GRU（BiGRU），然后是具有Swish激活函数的dense层。另一方面，解码器（D）由dense层和两个BiGRU层组成。解码器的输出是高光谱向量，表示为D(Ξ(xi))，具有与原始向量相同的维度。

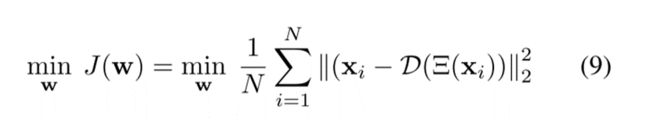
所提出的AE-BiGRU-Swish具有两个明显的特征：AE结构提供的非线性低维表示能力和使用Swish激活函数训练的BiGRU结构进行的系列预测。

实验

实验过程

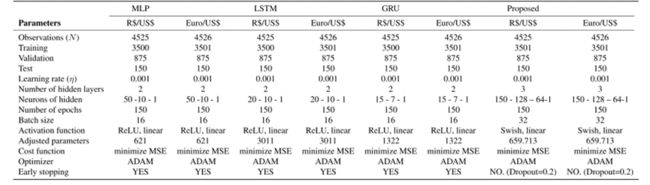
本研究旨在评估MLP，LSTM，GRU和AE-BiGRU-Swish神经网络模型在预测雷亚尔/美元和欧元/美元汇率的1，7，14，21和30天的时间范围内的表现。我们从yahoo finance中提取了这些系列，这些系列公开表示为汇率BRL=X（R$/US$）和EURUSD=X（Euro/US$）。这两个系列分别是2003年12月31日至2021年5月4日的雷亚尔/美元数据和2003年12月31日至2021年5月5日的欧元/美元数据的日平均值，分别为4525和4526次观测。
图1（a）和（B）说明了雷亚尔/美元和欧元/美元汇率的演变情况。

神经网络模型的参数和超参数如下表所示：

评估标准

平均绝对误差（MAE）、平均绝对百分比误差（MAPE）、均方误差（MSE）、均方根误差（RMSE）、方向精密度（ACCURACY）和Nash-Sutcliffe效率（CE），定义如下：

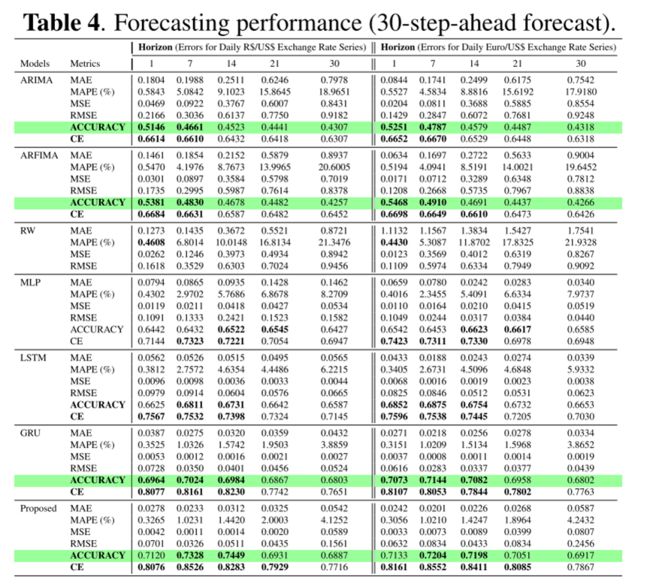
实验结果

比较了不同模型对30步前的预测结果如下表所示：

深度学习

Self-attention

背景

注意力机制的出现，使序列问题在预测每一个输出词的时候都可以关注不同的输入部分，更加接近解决问题的实际情况，提高了预测的准确率，但是原有的attention机制的实现都是借助于RNN、LSTM这样的循环神经网络，由于循环网络固有的缺陷，后面的计算依赖前面的输出，只能顺序计算，无法并行计算，当数据量大时，需要耗费很长的时间；之后又提出了借助于conv卷积网络的attention，可以实现并行计算，但是对于序列中距离较远的词语，学习它们之间的关系就又有问题了。

总的来说，在之前attention机制实现中遇到的问题主要是无法高效的并行计算，无法有效解决长依赖问题，因此提出了self attention 自注意力机制。

作用

本质上self attention依然是为了在解决序列问题中，预测不同的位置的输出时有着对输入不同的关注点，是注意力机制的一种实现方式。只不过它直接对输入序列进行计算，不再借助RNN或conv网络提取特征，创造性的提出了一种自己获取注意力，然后得到应该关注的特征的一种自注意力机制。

无论是依附于RNN还是conv，原始的注意力机制都需要借助其他网络提取特征，得到中间状态，然后利用注意力机制对各个状态赋予不同的关注程度。而self attention不再需要任何的其他网络结构帮助学习序列中的特征，直接对整个序列计算，实现注意力机制。从而就避免了RNN和conv网络所带来的无法并行计算或无法有效解决长依赖的问题。

实验证明，自注意力机制不仅带来了计算性能的提升，而且在许多领域的准确率上都有明显提升。
假如输入序列有三个词 ABC，对ABC词向量编码后，self attention做的就是在输出预测A词时候，对整体的加权关注，可以表示为：
A’= AWaa +BWab+ C*Wac
式中Waa，Wab，Wac就是通过selfattention计算得到的关注度矩阵

实现方式

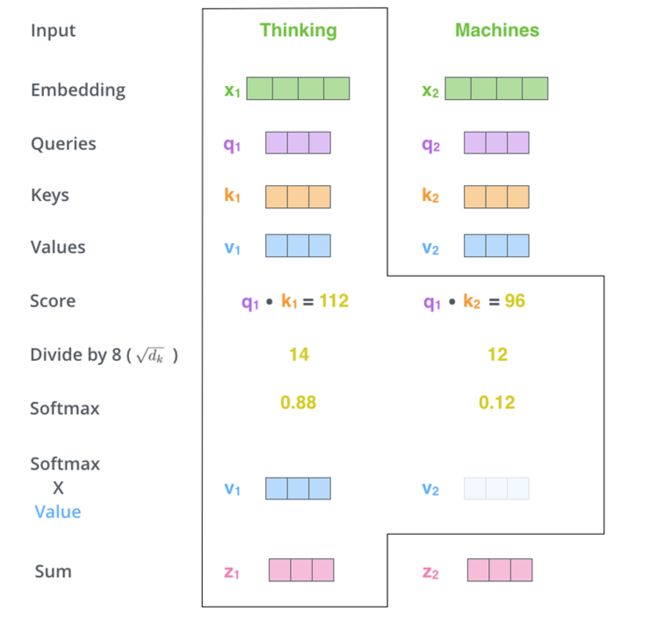
q\k\v分别对应attention机制中的Q\K\V，它们是通过输入词向量分别和W(Q)、W(K)、W(V)做乘积得到的。其目的主要是计算权值。

q与k做点乘、然后归一化，就得到权值（乘积越大，相似度越高，权值越高）。得到的两个权值分别与v相乘后，再相加就是输出。同理就可以得到另一个单词的输出。

以上是一个单词一个单词的输出，如果写成矩阵形式就是Q*K，得到的矩阵归一化直接得到权值。

简单self-attention模型的搭建

#self-attentiom模型的搭建：

from keras.preprocessing import sequence
from keras.datasets import imdb
from matplotlib import pyplot as plt
import pandas as pd
 
from keras import backend as K
from keras.engine.topology import Layer
 
 
class Self_Attention(Layer):
 
    def __init__(self, output_dim, **kwargs):
        self.output_dim = output_dim
        super(Self_Attention, self).__init__(**kwargs)
 
    def build(self, input_shape):
        # 为该层创建一个可训练的权重
        #inputs.shape = (batch_size, time_steps, seq_len)
        self.kernel = self.add_weight(name='kernel',
                                      shape=(3,input_shape[2], self.output_dim),
                                      initializer='uniform',
                                      trainable=True)
 
        super(Self_Attention, self).build(input_shape)  # 一定要在最后调用它
 
    def call(self, x):
        WQ = K.dot(x, self.kernel[0])
        WK = K.dot(x, self.kernel[1])
        WV = K.dot(x, self.kernel[2])
        print("WQ.shape",WQ.shape)
        print("K.permute_dimensions(WK, [0, 2, 1]).shape",K.permute_dimensions(WK, [0, 2, 1]).shape)
        QK = K.batch_dot(WQ,K.permute_dimensions(WK, [0, 2, 1]))
        QK = QK / (64**0.5)  #64*5是归一化的值，不同问题不一样
        QK = K.softmax(QK)
        print("QK.shape",QK.shape)
        V = K.batch_dot(QK,WV)
        return V
        
    def compute_output_shape(self, input_shape):
        return (input_shape[0],input_shape[1],self.output_dim)

在Keras上对IMDB进行简单的测试（不做Mask）：

from __future__ import print_function
from keras.preprocessing import sequence
from keras.datasets import imdb

max_features = 20000
maxlen = 80
batch_size = 32

print('Loading data...')
(x_train, y_train), (x_test, y_test) = imdb.load_data(num_words=max_features)
print(len(x_train), 'train sequences')
print(len(x_test), 'test sequences')

print('Pad sequences (samples x time)')
x_train = sequence.pad_sequences(x_train, maxlen=maxlen)
x_test = sequence.pad_sequences(x_test, maxlen=maxlen)
print('x_train shape:', x_train.shape)
print('x_test shape:', x_test.shape)

from keras.models import Model
from keras.layers import *

S_inputs = Input(shape=(None,), dtype='int32')
embeddings = Embedding(max_features, 128)(S_inputs)
# embeddings = Position_Embedding()(embeddings) # 增加Position_Embedding能轻微提高准确率
O_seq = Attention(8,16)([embeddings,embeddings,embeddings])
O_seq = GlobalAveragePooling1D()(O_seq)
O_seq = Dropout(0.5)(O_seq)
outputs = Dense(1, activation='sigmoid')(O_seq)

model = Model(inputs=S_inputs, outputs=outputs)
# try using different optimizers and different optimizer configs
model.compile(loss='binary_crossentropy',
              optimizer='adam',
              metrics=['accuracy'])

print('Train...')
model.fit(x_train, y_train,
          batch_size=batch_size,
          epochs=5,
          validation_data=(x_test, y_test))

总结

自注意力机制是注意力机制的变体，其减少了对外部信息的依赖，更擅长捕捉数据或特征的内部相关性。自注意力机制在文本中的应用，主要是通过计算单词间的互相影响，来解决长距离依赖问题。