数据结构第二弹---空间复杂度

1、算法效率

1.1、如何衡量一个算法的好坏

上一弹我们讲述了用时间复杂度（程序指令的执行次数）来衡量一个算法的好坏，这一弹我们讲述用空间复杂度来衡量算法的好坏。

2、空间复杂度

2.1、空间复杂度的概念

空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的
是变量的个数。
空间复杂度计算规则基本跟时间复杂度类似，也使用大O渐进表示法。

注意：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。

简而言之空间复杂度就是额外开辟的变量个数。

2.2、常见空间复杂度计算举例

1.

// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n)
{
	assert(a);
	for (size_t end = n; end > 0; --end)
	{
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

因为空间复杂度是额外开辟的变量个数
冒泡排序额外开辟的变量有exchange和交换数值函数的临时变量，但是两个变量都不会随着N的变化而变化，所以属于常量个变量，因此空间复杂度为O(1)。

2.

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
	if (n == 0)
		return NULL;

	long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
	fibArray[0] = 0;
	fibArray[1] = 1;
	for (int i = 2; i <= n; ++i)
	{
		fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
	}
	return fibArray;
}

因为空间复杂度是额外开辟的变量个数
该函数额外开辟的变量是动态开辟的指针变量fibArray，个数为n+1，根据大O渐进表示法，只保留最高阶数(N)，因此该函数空间复杂度为O(N)。

3.

// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{
	if (N == 0)
		return 1;

	return Fac(N - 1) * N;
}

因为空间复杂度是额外开辟的变量个数（包括新开辟的栈空间）
该函数为递归计算阶层的函数，函数执行时会先调用Fac(N-1)，再调用Fac(N-2)，直到N=0才停止，当中新开辟了N个栈空间(从N-1到0),因此该函数的空间复杂度为O(N)。

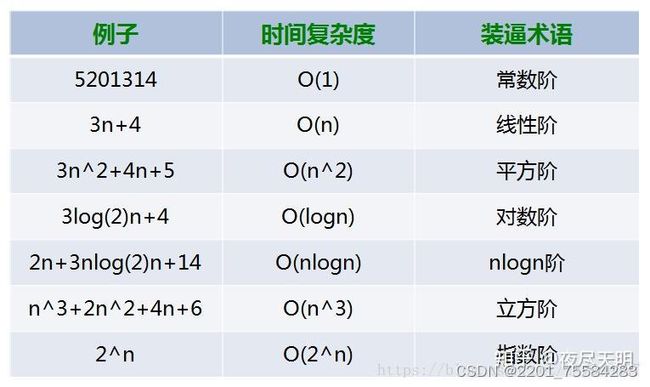
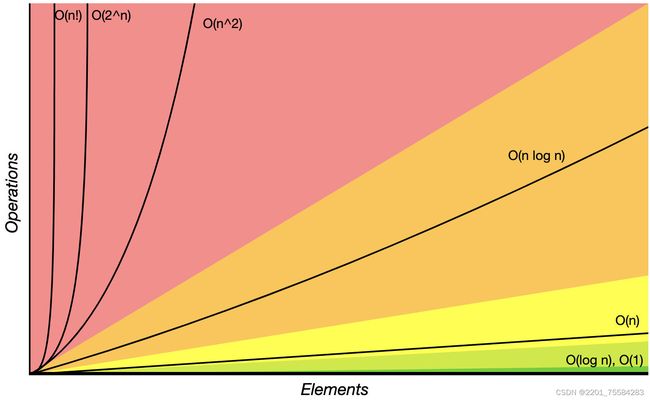
2.3、常见的复杂度对比

3、常见复杂度OJ练习

3.1、旋转数组

链接: 3.2 旋转数组OJ链接：https://leetcode-cn.com/problems/rotate-array/

思路一

void rotate(int* nums, int numsSize, int k) 
{
    k%=numsSize;
   //定义一个变长数组，用来存储交换的数
   int tmp[numsSize];
   int j=k;
   //将原数组前n-k拷贝到新数组的后面
   for(int i=0;i<numsSize-k;i++)
   {
       tmp[j++]=nums[i];
   }
   //将原数组后k个数据拷贝到新数组前k位置
   j=0;
   for(int i=numsSize-k;i<numsSize;i++)
   {
       tmp[j++]=nums[i];
   }
   //将新数组的数据拷贝到原来数组
   for(int i=0;i<numsSize;i++)
   {
       nums[i]=tmp[i];
   }
}

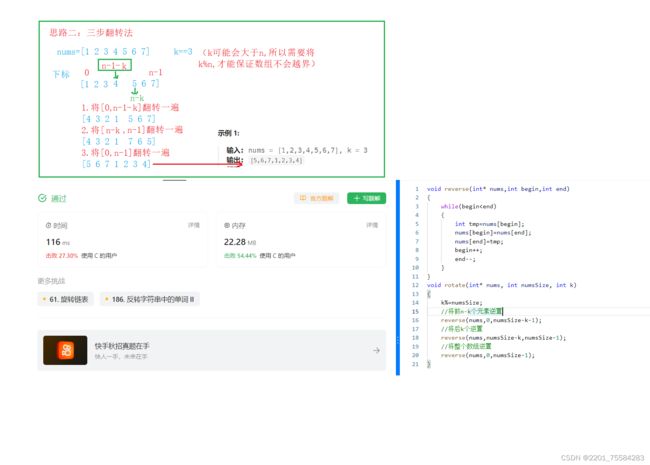
思路二

void reverse(int* nums,int begin,int end)
{
    while(begin<end)
    {
        int tmp=nums[begin];
        nums[begin]=nums[end];
        nums[end]=tmp;
        begin++;
        end--;
    }
}
void rotate(int* nums, int numsSize, int k) 
{
    k%=numsSize;
    //将前n-k个元素逆置
    reverse(nums,0,numsSize-k-1);
    //将后k个元素逆置
    reverse(nums,numsSize-k,numsSize-1);
    //将整个数组逆置
    reverse(nums,0,numsSize-1);
}

总结

本篇博客就结束啦，谢谢大家的观看，如果公主少年们有好的建议可以留言喔，谢谢大家啦！