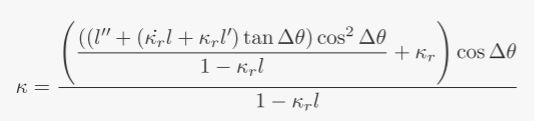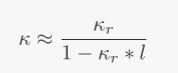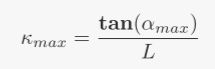分段加加速度之《Optimal Vehicle Path Planning Using Quadratic Optimization for Baidu Apollo Open Platform》解读
Apollo piecewise jerk path
参考资料来源:《Optimal Vehicle Path Planning Using Quadratic Optimization for Baidu Apollo Open Platform》一文、Apollo开发者社区、B站老王、csdn和知乎上的博客
注:本文章在于《Optimal Vehicle Path Planning Using Quadratic Optimization for Baidu Apollo Open Platform》一文的解读,大家在学习过程中请思考piecewise jerk path与EM planner的区别与联系
0 piecewise jerk path介绍
大家在学习过程中,可以将piecewise jerk path视作EM planner的路径规划的改进版,其处理的是静态和低速障碍物的path规划过程,动态障碍物依旧靠速度规划处理(不在该论文讨论范畴)。
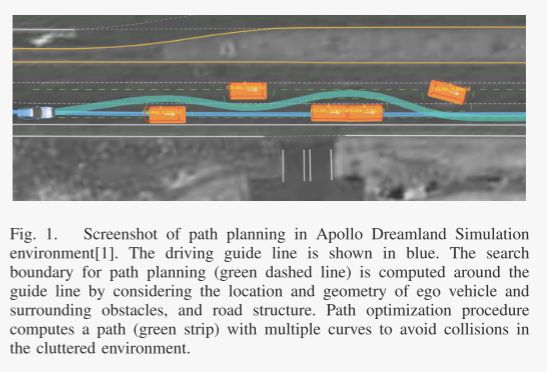
Fig.1为 path planning的仿真截图。蓝色代表着生成的参考线(依照该参考线生成自然坐标系),绿色虚框代表着车辆进行搜索的空间(也即路径边界),绿色代表着规划的路径。
在学习过程中,需要把握以下几个点:
- 参考线如何平滑
- 路径边界如何生成
- 路径优化的目标函数和约束条件是什么
- 与EM planner的联系与区别
1 基础知识
1.1 自行车模型
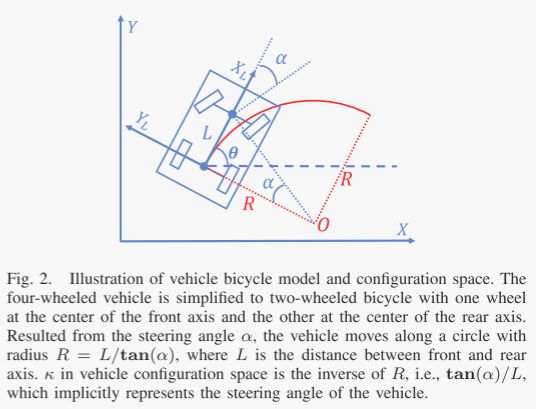
对于一辆车,我们可以将其抽象成一个自行车模型。一般而言,对于一个二维刚体,描述其状态需要 ( x , y , θ ) (x,y,\theta) (x,y,θ)三个状态量表述即可,而Apollo同时又考虑 κ \kappa κ曲率这一物理量,其可以想象成车辆转弯半径 R R R的倒数,同时根据图中几何关系有 R = L / t a n ( α ) R=L/tan(\alpha) R=L/tan(α)( L L L为前后轴距离, α \alpha α为转向角),所以 κ \kappa κ曲率也隐含着转向角 α \alpha α的信息
1.2 曲率约束的推导
关于曲率约束的推导论文给的比较模糊,所以这里推导一下(属于4 路径优化中的约束条件模块)。
注:这个公式其实就是自然坐标系与笛卡尔坐标系的转换公式,大家可以通过老王视频或者下面博客学习https://blog.csdn.net/u013468614/article/details/108748016.(这里假设你会了,直接往下看就好)。
这里解释几个不常见的符号:
- κ \kappa κ : 车辆轨迹 ( s i , l i ) (s_{i},l_{i}) (si,li)对于的曲率
- κ r \kappa_{r} κr : 车辆轨迹 ( s i , l i ) (s_{i},l_{i}) (si,li)投影到参考线对于的投影点 p r p_{r} pr的曲率
- κ ˙ r \dot\kappa_{r} κ˙r : κ r \kappa_{r} κr的倒数
- Δ θ \Delta\theta Δθ :车辆航向方向与点 p r p_{r} pr的切线方向之间的角度差。
提出两点假设即可推出简化版公式:
- 假设车辆的航向角与相应点处的引导线的方向相同,因此 Δ θ = 0 \Delta\theta = 0 Δθ=0。
- l ′ ′ l^{''} l′′数值上很小(约为 1 0 − 2 10^{-2} 10−2),假定为0。
根据这两点假设,带入a中的曲率转换公式即可推出曲率简化公式
根据1.1介绍的自行车模型,可以推出 κ m a x \kappa_{max} κmax
这个论文公式给的比较抽象,其实就是自车的转角不能超过最大转角。大家可以通过下面的不等式推出论文结论 ∣ κ r ∣ 1 − κ r l ≤ tan α m a x L \frac{\left |\kappa _{r}\right |}{1-\kappa _{r}l}\le \frac{\tan \alpha _{max}}{L} 1−κrl∣κr∣≤Ltanαmax(转向角有正有负所以加绝对值,曲率都要小于最大曲率)
2 参考线平滑算法
关于参考线需要思考几个问题:
Q :参考线真实长什么样子,是连续的嘛?
A :真实的参考线实际上一系列的点组成,也即 p 0 = ( x 0 , y 0 ) , . . . , p n − 1 = ( x n − 1 , y n − 1 ) p_{0} = (x_{0},y_{0}),...,p_{n-1} = (x_{n-1},y_{n-1}) p0=(x0,y0),...,pn−1=(xn−1,yn−1)
Q : 参考线为什么要平滑?
A :一般来说参考线是选择道路中心线作为参考线,为了提高后面优化路径解的质量,需要对原来的参考线进行平滑。
Q :平滑意味着什么?
A :平滑意味着其曲率及其变化率较小(也就是越直越好),同时平滑后参考线要在道路边界
好的,思考完上述问题,我们开始进行参考线平滑。其本质是一个优化问题,输入是原始的参考线(一系列点),输出平滑后的参考线(还是一系列点)
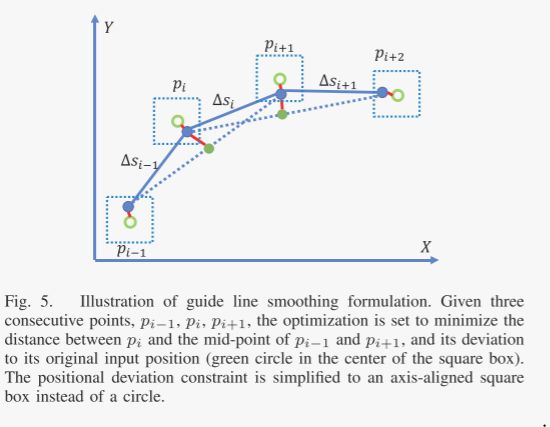
如图五所示,绿色空心代表原始的参考线,蓝色实心代表平滑后参考线,绿色实心代表间隔一个的相邻两个点连线的中点。
以 p i − 1 , p i , p i + 1 p_{i-1},p_{i},p_{i+1} pi−1,pi,pi+1优化为例:
- 目标函数1: p i p_{i} pi距离 p i − 1 p_{i-1} pi−1和 p i + 1 p_{i+1} pi+1的中点最小
- 目标函数2:优化前和优化后的 p i p_{i} pi的距离尽可能小
- 约束条件:优化后和优化前的距离范围在蓝色虚框范围内
3 路径边界生成
在路径边界生成介绍之前,请大家思考几个问题
Q:EM planner中决策(向左或向右变道)使用的何种思想,而piecewise jerk path中的决策如何生成呢?
A: EM planner中决策采用的是动态规划的思想,本质上是一个轻决策算法,而piecewise jerk path中的决策采用的是一种基于交通规则、自车状态、堵塞障碍物信息的决策树算法,其输出会告诉车辆一个可行区域
Q:路径边界的形式具体是如何的?
A:其形式可以 l B l_{B} lB,也即,给定一个 s i s_{i} si,其输出是一个安全边界 ( l m i n , l m a x ) (l_{min},l_{max}) (lmin,lmax)
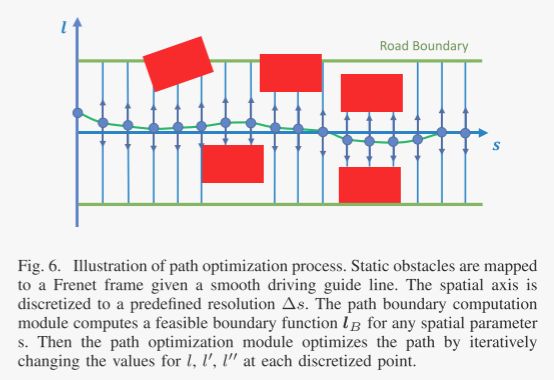
具体形式就是长成下面这样,根据道路边界、障碍物、车自身、将s离散化,输出一条路径边界(后续会在该区域内优化)
4 路径优化
在开始路径优化过程中,请大家思考下几个问题
Q:EM planner中在DP过程后得到了一个粗解和可行区域,之后如何进行路径优化?对于piecewise jerk path中如何处理呢?
A:EM planner中在DP之后采用QP算法对粗解进行平滑,piecewise jerk path与EM planner类似也是使用QP算法,不同的是目标函数和约束条件有些不同,同时还多加一个相邻点jerk恒定的假设
Q:对于一个路径 l ( s ) l(s) l(s),需要考虑哪些因素进行优化
A:可以归结为以下几点
1.安全无碰撞
2.车辆尽量靠近车道中心线
3.横向位移的变化缓慢(舒适)
4.车辆尽量靠近与其相应路径边界中心。
综上,可以将目标函数写为如下形式:前四项项保证光滑性、以及横向位移的变化缓慢。最后一项保证车辆尽量靠近与其相应路径边界中心
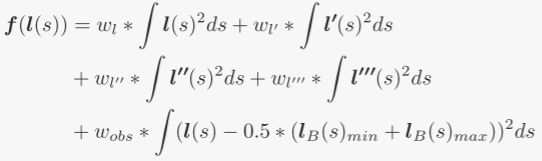
另外这也并非完整形式,我们需要将其写成离散形式,引入相邻点jerk恒定的假设,利用下述公式近似计算jerk(同时假设相邻点恒定,注意不同对点之间的jerk是不一样的),故可以写成离散形式
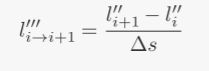
- 目标函数离散形式:注意第四项利用的jerk恒定假设得到
- 连续性约束:关于连续性约束(类似于泰勒展开,就不细说了)
- 安全性约束:规划的路径必须在可行区域内,从而保证安全无碰撞
- 曲率约束:自车的转角不能超过最大转角
5 与EM planner的联系与区别
- 该论文属于EM planner的path规划过程,不包括速度规划过程,本质上是对EM planner的path规划的改进
- EM planner的决策过程是基于DP思想的,属于一种轻决策算法,而分段加加速度法决策是基于规则生成
- 二者处理问题的思想类似,都是找一条质量好的 l ( s ) l(s) l(s)。思路大概为决策可行空间,在可行空间中优化路径。不同的是分段加加速度法提出了相邻点之间jerk恒定,简化了问题