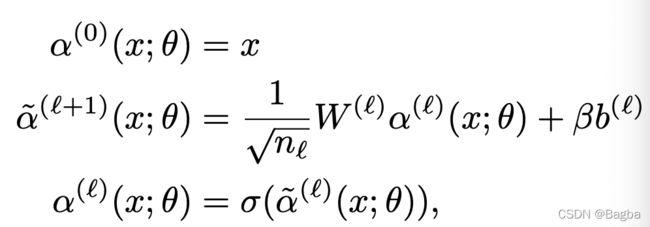Neural Tangent Kernel 理解（一）原论文解读

• 欢迎关注WX公众号，每周发布论文解析：PaperShare,
  点我关注

NTK的理解系列 暂定会从（一）论文解读，（二）kernel method基础知识，（三）神经网络表达能力，（四）GNN表达能力 等方面去写。当然，可能有的部分会被拆开为多个小部分来写，毕竟每一个点拿出来都可以写本书了。

（本人各个系列旨在让复杂概念通俗易懂，力求获得进一步理解）

---

Neural Tangent Kernel (NTK) 理论由 [1] 提出，后续有很多跟进的研究工作，比如和我自己领域比较相关的，Simon Du老师提出的Graph neural tangent kernel [2].

NTK在深度学习理论中是很有意思的，通过学习该理论和相关论文，我们能够得到许多启发，所以我准备通过记录自己学习NTK的过程来巩固和分享一些自己的理解。由于本文主要是以自己的视角来看，难免有疏漏，错误和偏见。

我们按照论文的顺序来叙述。

（一） Neural Tangent Kernel 目的

Abstract第一句话：

无限宽的ANN初始化等价于高斯过程，所以可以和Kernel method联系起来。然后作者证明了，训练过程，也可以用一个kernel method来描述，并且能够通过kernel gradient descent来训练，这个kernel就是NTK。

论文目的总结起来就是：

1. 理论证明了可以 用NTK来描述ANN训练过程。
2. 理论证明了可以 用Kernel gradient descent in funcion space来训练ANN。
3. 理论证明了收敛性.
4. 理论证明了当数据服从某些特性时，NTK是p.d.的。
5. 用least-squares regression举了一个例子。
6. 实验结果体现了NTK的一些理论分析。

（二） Neural Tangent Kernel 预备知识

为了方便描述，首先引入一些数学符号和公式定义。

1. 定义一个有 L 层的ANN：

$$F^{(L)}:{\mathbb{R}}^P\to \mathcal{F}$$
即，将维度为P的参数$\theta$映射到一个属于函数域$\mathcal{F}$的函数$f_{\theta }$。$f_{\theta }$即:参数为$\theta$的ANN。这里$P={\sum }_{l=0}^{L-1}(n_l+1)(n_{l+1})$, $n_l$为第$l$层的输入维度。

2. 定义每一层NN：

3. Kernel gradient.

要理解这部分内容，需要像泛函分析等的数学基础知识。这里，我用类比简单概念来帮助理解。比如，首先我们将$f_{\theta }$想象成一个变量，这个变量的值域是$\mathcal{F}$，目标是找到一个optimal的$f_{\theta }$，使得cost最小。

3.1 定义cost：$C:\mathcal{F}\to \mathbb{R}$。

3.2 定义 multi-dimensional kernel K: ${\mathbb{R}}^{n_0}\times {\mathbb{R}}^{n_0}\to {\mathbb{R}}^{n_L}\times {\mathbb{R}}^{n_L}$, 且，$K(x,x^{\prime })=K(x^{\prime },x)$.

3.3 定义 bilinear map on $\mathcal{F}$ 或叫seminorm $||\cdot |{|}_{p^{in}}$:
$$⟨f,g{⟩}_{p^{in}}:={\mathbb{E}}_{x\sim p^{in}}[f(x{)}^{T}g(x^{\prime })].$$

3.4 定义基于kernel K的 bilinear map on $\mathcal{F}$:
$$⟨f,g{⟩}_K:={\mathbb{E}}_{x,x^{\prime }\sim p^{in}}[f(x{)}^{T}K(x,x^{\prime })g(x^{\prime })].$$
即，求一个在输入概率分布$p^{in}$下的基于kernel的线性变换下的期望。

3.5 定义$\mathcal{F}$的对偶${\mathcal{F}}^{\ast }$: $\mu :\mathcal{F}\to \mathbb{R}$, where $\mu =⟨d,\cdot {⟩}_{p^{in}}$，$d\in \mathcal{F}$. 这里可以把$\mu$当成一个输入为$f$的函数，或者是一个线性变换。

3.6 定义一个map ${\Phi }_K$:${\mathcal{F}}^{\ast }\to \mathcal{F}$, 利用kernel的性质: $K_{i,\cdot }(x,\cdot )\in F$, 则可以利用${\Phi }_K$将$\mu$映射为$f$：$f_{\mu }={\Phi }_K(\mu )$，对于每一个$i$, 有：$f_{\mu ,i}(x)=\mu K_{i,\cdot }(x,\cdot )=⟨d,K_{i,\cdot }(x,\cdot ){⟩}_{p^{in}}$

3.6 定义cost function $C$关于$f$的泛函导数（functional derivative）。给定数据集$x_1,...,x_n$, 那么在点$f_0\in F$处的导数${\partial }_f^{in}C{|}_{f_0}=⟨d{|}_{f_0},\cdot ⟩$, 这里$d{|}_{f_0}\in F$.

3.7 定义kernel gradient ：${\nabla }_{K}C{|}_{f_0}\in F={\Phi }_K\left({\partial }_f^{in}C{|}_{f_0}\right)$. 这里可以把$x$的范围从数据集1-n扩展到任意$x$:

那么，$f(t)$ 就可以进行kernel gradient descent，只要满足：

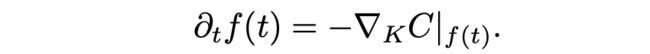
对cost function的进行梯度更新的梯度：

这里，可以保证收敛，因为kernel $K$是p.d.的，只要C是convex，且bounded，则当$t\to \infty$ 时，$f(t)$就可以收敛到全局最优。

明天继续。。。。码我自己的论文去了。。

[1] Jacot, Arthur, Franck Gabriel, and Clément Hongler. “Neural tangent kernel: Convergence and generalization in neural networks.” arXiv preprint arXiv:1806.07572 (2018).
[2] Du, Simon S., et al. “Graph neural tangent kernel: Fusing graph neural networks with graph kernels.” Advances in Neural Information Processing Systems 32 (2019): 5723-5733.