力扣刷题-python-回溯算法-1(回溯算法模板、题型)
文章目录
-
- 1.回溯算法
- 2.回溯算法模板
- 3.回溯实例(77、216、17、39、40、131、93、78、90、491、46、47)
- 4.总结
1.回溯算法
回溯算法的本质就是穷举,最多再加上剪枝,剪掉一部分不必要的。
关于排列组合的区别,组合无序,排列有序
回溯算法解决问题都可以抽象为树形结构(N叉树),树的宽度代表集合的大小,树的深度代表递归的深度,树的高度是有限的,也就是递归是有终止条件的。
2.回溯算法模板
void backtracking(参数) :
if (终止条件) :
存放结果
return
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)):
处理节点
backtracking(路径,选择列表) # 递归
回溯,撤销处理结果
3.回溯实例(77、216、17、39、40、131、93、78、90、491、46、47)
77. 组合 - 力扣(LeetCode) (leetcode-cn.com)


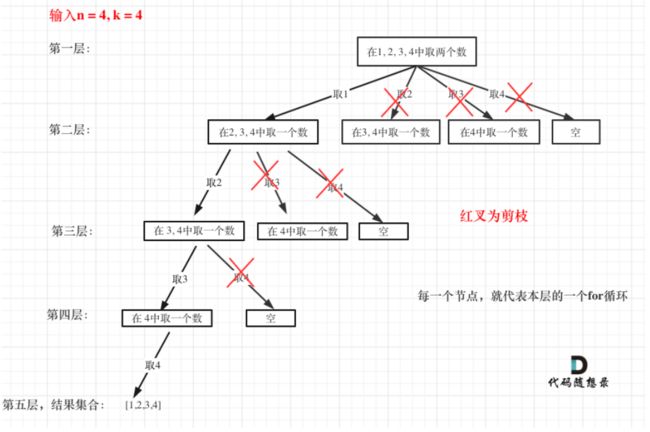
剪枝需要在for里面做处理
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
def backtracking(i):
if not len(path)-k: return res.append(path[:])
for j in range(i,n-(k-len(path)-1)):
#if j>n-(k-len(path)):break #剪枝
path.append(j+1)
backtracking(j+1)
path.pop()
res=[] #存放符合条件结果的集合
path=[] #用来存放符合条件结果
backtracking(0)
return res
216. 组合总和 III - 力扣(LeetCode) (leetcode-cn.com)
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
def backtracking(sumer,i):
if not sumer and not len(path)-k:return res.append(path[:])
for j in range(i,9):
if sumer-j-1<0:break #剪枝
path.append(j+1)
backtracking(sumer-j-1,j+1)
path.pop()
path =[]
res = []
backtracking(n,0)
return res
17. 电话号码的字母组合 - 力扣(LeetCode) (leetcode-cn.com)
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
def backtracking(digits):
if not digits:return res.append(''.join(path)) #如果为空开始收集数据
index = int(digits[0])-2
for i in nums[index]:
path.append(i)
backtracking(digits[1:])
path.pop()
nums=['abc','def','ghi','jkl','mno','pqrs','tuv','wxyz']
path =[]
res = []
backtracking(digits)
return res if digits else []
39. 组合总和 - 力扣(LeetCode) (leetcode-cn.com)
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
def backtacking(target,index):
if not target: return res.append(path[:])
for i in range(index,len(candidates)):
if target-candidates[i]<0:return #剪枝
path.append(candidates[i])
backtacking(target-candidates[i],i)
path.pop()
res, path = [], []
candidates.sort()
backtacking(target,0)
return res
40. 组合总和 II - 力扣(LeetCode) (leetcode-cn.com)
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
def backtacking(target,index):
if not target: return res.append(path[:])
for i in range(index,len(candidates)):
if target-candidates[i]<0: break #剪枝
if i>index and not candidates[i]-candidates[i-1]:continue #剪掉重复项
path.append(candidates[i])
backtacking(target-candidates[i],i+1)
path.pop()
res, path = [], []
candidates.sort() #排序方便后面的回溯
backtacking(target,0)
return res
131. 分割回文串 - 力扣(LeetCode) (leetcode-cn.com)
class Solution:
def partition(self, s: str) -> List[List[str]]:
def backtracking(index):
if not index-len(s): return res.append(path[:])
for i in range(index,len(s)):
selectS= s[index:i+1]
if selectS!=selectS[::-1]:continue
path.append(selectS)
backtracking(i+1)
path.pop()
res, path = [], []
backtracking(0)
return res
93. 复原 IP 地址 - 力扣(LeetCode) (leetcode-cn.com)
class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
def backtracking(index,count):
if not index- len(s) and not count:return res.append('.'.join(path[:]))
for i in range(index,len(s)):
temp = s[index:i+1]
if count<0: break #大于4个的 跳出
if int(temp)>255 or len(temp)>1 and not int(temp[0]):break #判断是否为有效ip
path.append(s[index:i+1])
backtracking(i+1,count-1)
path.pop()
res, path = [], []
backtracking(0,4)
return res
78. 子集 - 力扣(LeetCode) (leetcode-cn.com)
不同于前面的是每次结果,它都会收集

class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
def backtracking(nums):
res.append(path[:])
if not len(nums): return
for i in range(len(nums)):
path.append(nums[i])
backtracking(nums[i+1:])
path.pop()
res, path = [], []
backtracking(nums)
return res
90. 子集 II - 力扣(LeetCode) (leetcode-cn.com)
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
def backtracking(nums):
res.append(path[:])
if not nums:return
for i in range(len(nums)):
if i>0 and not nums[i]-nums[i-1]:continue#剪枝
path.append(nums[i])
backtracking(nums[i+1:])
path.pop()
res, path = [], []
nums.sort()
backtracking(nums)
return res
491. 递增子序列 - 力扣(LeetCode) (leetcode-cn.com)
class Solution:
def findSubsequences(self, nums: List[int]) -> List[List[int]]:
def backtracking(nums):
if len(path)>1:res.append(path[:]) #只取内元素个数大于等于2
if not nums:return 0
# 深度遍历中每一层都会有一个全新的usage_list用于记录本层元素是否重复使用
usage_list = set()
for i in range(len(nums)):
#递增的保证
if path and nums[i]<path[-1]:continue #判断是为递增
if nums[i] in usage_list:continue #去除重复项
usage_list.add(nums[i])
path.append(nums[i])
backtracking(nums[i+1:])
path.pop()
res, path = [], []
backtracking(nums)
return res
46. 全排列 - 力扣(LeetCode) (leetcode-cn.com)
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
def backstacking(nums):
if not nums:return res.append(path[:])
for i in range(len(nums)):
path.append(nums[i])
backstacking(nums[:i]+nums[i+1:])
path.pop()
res, path = [], []
backstacking(nums)
return res
47. 全排列 II - 力扣(LeetCode) (leetcode-cn.com)
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
def backtracking(nums):
if not nums:return res.append(path[:])
dedup= set() #去掉某一层一样的
for i in range(len(nums)):
if nums[i] in dedup:continue
dedup.add(nums[i])
path.append(nums[i])
backtracking(nums[:i]+nums[i+1:])
path.pop()
res, path= [], []
backtracking(nums)
return res
4.总结
还留下三道困难题,明天再看了,如果明天看完比较早,那就往下看贪心算法,希望一切顺利!