Julia集和Mandelbrot集绘制(C++)
在本文中, 我们主要考虑两个特殊的迭代, 即分形几何中非常有名的Julia集和Mandelbrot集. 两者均是由复函数 f ( z ) = z 2 + C f(z)=z^2+C f(z)=z2+C迭代实现的, 但在具体实现上有所不同.
Julia集
算法描述
输入:绘图区域[a,b] x [c,d], 复常数C, 逃逸半径M, 最大迭代次数N, 区间分割数n
输出:格点的迭代次数矩阵R
R初始化为全零矩阵- 将
[a,b]分为n等份,得到向量x - 将
[c,d]分为n等份,得到向量y - 用
x + i*y生成网格,得到矩阵z - 找出
z中模大于M的元素,得到下标向量t - 将
z(t)设置为NaN - 循环
N次:- 将
z替换为z^2 + C - 找出
z中模大于M的元素,得到下标向量t - 将
z(t)设置为NaN - 将
R(t)设置为当前循环次数i
- 将
- 找出
z中模不是NaN的元素,得到下标向量t - 将
R(t)设置为N - 返回
R
实现代码
#include 测试案例
取 a = c = − 1.5 , b = d = 1.5 , C = − 0.46 + 0.57 i , M = 2 , N = 100 , n = 512 a=c=-1.5,b=d=1.5,C=-0.46+0.57{\rm i},M=2,N=100,n=512 a=c=−1.5,b=d=1.5,C=−0.46+0.57i,M=2,N=100,n=512, 可利用Origin绘制Julia集如图所示:

Mandelbrot集
算法描述
输入:绘图区域[a,b] x [c,d], 逃逸半径M, 最大迭代次数N, 区间分割数n
输出:格点的迭代次数矩阵R
R初始化为全零矩阵z0赋值为z- 将
[a,b]分为n等份,得到向量x - 将
[c,d]分为n等份,得到向量y - 用
x + i*y生成网格,得到矩阵z - 找出
z中模大于M的元素,得到下标向量t - 将
z(t)设置为NaN - 循环
N次:- 将
z替换为z^2 + z0 - 找出
z中模大于M的元素,得到下标向量t - 将
z(t)设置为NaN - 将
R(t)设置为当前循环次数i
- 将
- 找出
z中模不是NaN的元素,得到下标向量t - 将
R(t)设置为N - 返回
R
实现代码
/*
* Mandelbrot集绘制
* [xa,xb]: 绘图区域的x范围
* [ya,yb]: 绘图区域的y范围
* M : 逃逸半径
* N : 最大迭代数
* n : 区间分割数
*/
umat Mandelbrot(double xa, double xb, double ya, double yb, double M = 2, unsigned N = 100, unsigned n = 512)
{
++n;
umat R = zeros<umat>(n, n);
rowvec x(linspace(xa, xb, n));
vec y(linspace(ya, yb, n));
cx_mat z(repmat(x, n, 1), repmat(y, 1, n)), c(z);
unsigned k(0);
uvec ind = find(abs(z) > M);
for (auto &i : ind)
z.at(i) = NAN;
while (++k != N)
{
ind = find(abs((z %= z) += c) > M);
for (auto &i : ind)
{
z.at(i) = NAN;
R.at(i) = k;
}
}
ind = find_finite(z);
for (auto &i : ind)
R.at(i) = N;
return R;
}
测试案例
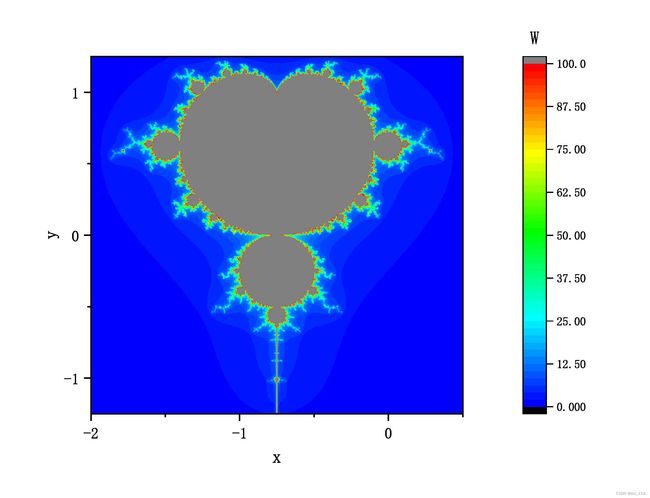
取 a = − 2 , b = 0.5 , c = − 1.25 , d = 1.25 , M = 2 , N = 100 , n = 512 a=-2,b=0.5,c=-1.25,d=1.25,M=2,N=100,n=512 a=−2,b=0.5,c=−1.25,d=1.25,M=2,N=100,n=512, 可绘制Mandelbrot集如图所示: