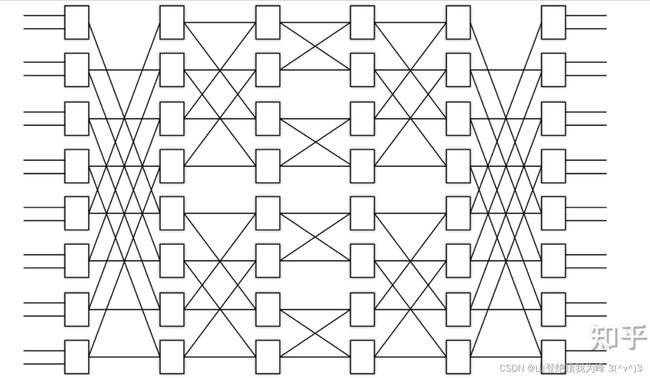
FHE 的槽置换:Benes Network
参考文献:
- [SV11] Smart N P, Vercauteren F. Fully homomorphic SIMD operations[J]. Designs, codes and cryptography, 2014, 71: 57-81.
- [GHS12] Gentry C, Halevi S, Smart N P. Fully homomorphic encryption with polylog overhead[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 465-482.
- [HS13] Halevi S, Shoup V. Design and implementation of a homomorphic-encryption library[J]. IBM Research (Manuscript), 2013, 6(12-15): 8-36.
- [HS14] Halevi S, Shoup V. Algorithms in helib[C]//Advances in Cryptology–CRYPTO 2014: 34th Annual Cryptology Conference, Santa Barbara, CA, USA, August 17-21, 2014, Proceedings, Part I 34. Springer Berlin Heidelberg, 2014: 554-571.
- 多项式和有限域的Galois群 - 知乎
- 有限 Abel 群结构定理 - 知乎
- 神奇的Banyan Network - 知乎
- Hall 定理 & 正则二分图的完美匹配
- 匈牙利算法的实现原理是什么? - 知乎
文章目录
- SIMD & Rotate
-
- SIMD Packing
- Slot Rotation
- Permutaion Network
-
- Hyper-Rectangles
- Cloning
- Batch Selection
- Shift Network
- Shift-Networks
-
- Benes Network
- General Benes Network
SIMD & Rotate
假设 P P P 是素域,令 E E E 是 X m − 1 X^m-1 Xm−1 的在素域 P P P 上的分裂域,则 E / P E/P E/P 是代数单扩张:任意本原根 ζ m \zeta_m ζm,扩域 E = P ( ζ m ) E=P(\zeta_m) E=P(ζm),循环群 G = ( ζ m ) G=(\zeta_m) G=(ζm)
- 如果 c h a r ( P ) = p char(P)=p char(P)=p,那么扩张次数 [ E : Z p ] = r [E:\mathbb Z_p]=r [E:Zp]=r,它是满足 p r = 1 ( m o d m ) p^r =1 \pmod m pr=1(modm) 的最小整数,并且 ζ m \zeta_m ζm 在 P P P 上的极小多项式为 f ( x ) = ( x − ζ m ) ( x − ζ m p ) ⋯ ( x − ζ m p r − 1 ) f(x)=(x-\zeta_m)(x-\zeta_m^p)\cdots(x-\zeta_m^{p^r-1}) f(x)=(x−ζm)(x−ζmp)⋯(x−ζmpr−1),这里的 ζ m p j − 1 \zeta_m^{p^j-1} ζmpj−1 是本原单位根的共轭
- 如果 c h a r ( P ) = 0 char(P)=0 char(P)=0,那么扩张次数 [ E : Q ] = ϕ ( m ) [E:\mathbb Q]=\phi(m) [E:Q]=ϕ(m),并且 ζ m \zeta_m ζm 在 P P P 上的极小多项式 ϕ m ( x ) = ∏ j ∈ Z m ∗ ( x − ζ m j ) \phi_m(x)=\prod_{j \in \mathbb Z_m^*}(x-\zeta_m^j) ϕm(x)=∏j∈Zm∗(x−ζmj) 称为分圆多项式,它是 Q [ x ] \mathbb Q[x] Q[x] 上的不可约多项式, E = Q ( ζ m ) E=\mathbb Q(\zeta_m) E=Q(ζm) 称为分圆域
令 ϕ m ( x ) \phi_m(x) ϕm(x) 是分圆多项式, ζ m \zeta_m ζm 是本原单位根,分圆数域 K = Q ( ζ m ) ≅ Q [ x ] / ( ϕ m ( x ) ) K=\mathbb Q(\zeta_m) \cong \mathbb Q[x]/(\phi_m(x)) K=Q(ζm)≅Q[x]/(ϕm(x)),它的整数环是 O K = Z [ ζ m ] ≅ Z [ x ] / ( ϕ m ( x ) ) \mathcal O_K = \mathbb Z[\zeta_m] \cong \mathbb Z[x]/(\phi_m(x)) OK=Z[ζm]≅Z[x]/(ϕm(x)),其中 x = ζ m x=\zeta_m x=ζm,令 N = deg ϕ m ( x ) = ϕ ( m ) N=\deg\phi_m(x)=\phi(m) N=degϕm(x)=ϕ(m)
根据 Galois Theory, K K K 是可分多项式 x n − 1 x^n-1 xn−1 的分裂域,因此 K / Q K/\mathbb Q K/Q 是 Galois 扩张,并且 G a l ( K / Q ) ≅ Z m ∗ Gal(K/\mathbb Q) \cong \mathbb Z_m^* Gal(K/Q)≅Zm∗ 是阿贝尔群,于是 K / Q K/\mathbb Q K/Q 是阿贝尔扩张。全部的自同构都落在 Galois 群内 A u t ( K ) = G a l ( K / Q ) Aut(K) = Gal(K/\mathbb Q) Aut(K)=Gal(K/Q),形如 κ j : f ( x ) ↦ f ( x j ) , ∀ j ∈ Z m ∗ \kappa_j: f(x) \mapsto f(x^j),\forall j \in \mathbb Z_m^* κj:f(x)↦f(xj),∀j∈Zm∗
对于有限域 F = G F ( p d ) F=GF(p^d) F=GF(pd),它是可分多项式 x p d − x x^{p^d}-x xpd−x 的分裂域,因此 F / Z p F/\mathbb Z_p F/Zp 是 Galois 扩张,并且 G a l ( F / Z p ) = ( κ p ) Gal(F/\mathbb Z_p)=(\kappa_p) Gal(F/Zp)=(κp) 是循环群,其中 κ p : x ↦ x p \kappa_p:x \mapsto x^p κp:x↦xp 是 Frobenius 映射,此时 F / Z p F/\mathbb Z_p F/Zp 是循环扩张。
令 A = Z [ x ] / ( ϕ m ( x ) ) \mathbb A = \mathbb Z[x]/(\phi_m(x)) A=Z[x]/(ϕm(x)),我们令 A p \mathbb A_p Ap 是明文空间, A q \mathbb A_q Aq 是密文空间,其中 p p p 是较小素数(比如 32 比特素数),而 q q q 是很大的模数(可以是素数,也可以是一些素数乘积)。我们用 A q \mathbb A_q Aq 模拟 A \mathbb A A 的运算,对于明文 a ∈ A p a \in \mathbb A_p a∈Ap,在编码到 A q \mathbb A_q Aq 中的 a + p e a+pe a+pe,只要运算过程中 a + p e a+pe a+pe 的规模没有越过 q q q,那么 A q \mathbb A_q Aq 确实正确地模拟了 A \mathbb A A 上的运算,从而再模掉 p p p 即可得到 A p \mathbb A_p Ap 中的计算结果。
SIMD Packing
虽然 ϕ m ( x ) \phi_m(x) ϕm(x) 在 Q \mathbb Q Q 上不可约,但是在有限域 Z p \mathbb Z_p Zp 上是可约的: ϕ m ( x ) \phi_m(x) ϕm(x) 拥有次数 d d d 的素因子,当仅当 m ∣ p d − 1 m|p^d-1 m∣pd−1(此时扩域 G F ( p d ) GF(p^d) GF(pd) 中包含 m m m 次本原单位根),多项式分解为 ϕ m ( x ) = ∏ i = 1 l F i ( x ) ( m o d p ) \phi_m(x)=\prod_{i=1}^{l}F_i(x) \pmod p ϕm(x)=∏i=1lFi(x)(modp),其中 l = N / d l=N/d l=N/d, deg F i = d , ∀ i \deg F_i=d,\forall i degFi=d,∀i
整环 Z [ x ] \mathbb Z[x] Z[x] 的理想 p = ( p , ϕ m ( x ) ) \mathscr p=(p,\phi_m(x)) p=(p,ϕm(x)), p i = ( p , F i ( x ) ) \mathscr p_i=(p,F_i(x)) pi=(p,Fi(x)),易知 p = ⋂ i p i \mathscr p=\bigcap_i \mathscr p_i p=⋂ipi,根据 CRT 得到:
Z p [ x ] / ( ϕ m ( x ) ) ≅ ∏ i = 1 l Z p [ x ] / ( F i ( x ) ) \mathbb Z_p[x]/(\phi_m(x)) \cong \mathbb \prod_{i=1}^l \mathbb Z_p[x]/(F_i(x)) Zp[x]/(ϕm(x))≅∏i=1lZp[x]/(Fi(x))
由于 F i ( x ) F_i(x) Fi(x) 是不可约的,因此 L i = Z p [ x ] ( F i ( x ) ) ≅ G F ( p d ) \mathbb L_i=\mathbb Z_p[x](F_i(x)) \cong GF(p^d) Li=Zp[x](Fi(x))≅GF(pd) 都是同一个有限域。我们要求明文模数 p p p 足够大,使得槽的数量 l = N / d l=N/d l=N/d 足够多。
假设消息空间是子域 K n ≤ G F ( p d ) \mathbb K_n \le GF(p^d) Kn≤GF(pd),满足 [ K n : Z p ] = n ∣ d [\mathbb K_n:\mathbb Z_p]=n|d [Kn:Zp]=n∣d。定义映射 ψ n , i : K n → L i \psi_{n,i}: \mathbb K_n \to \mathbb L_i ψn,i:Kn→Li 是同态嵌入(当 d = n d=n d=n 时是自同构),编码函数 ψ n : K n l → A p \psi_n:\mathbb K_n^l \to A_p ψn:Knl→Ap 定义为
ψ n : ( m 1 , ⋯ , m l ) ↦ ( ψ n , 1 ( m 1 ) , ⋯ , ψ n , l ( m l ) ) \psi_n: (m_1,\cdots,m_l) \mapsto (\psi_{n,1}(m_1),\cdots,\psi_{n,l}(m_l)) ψn:(m1,⋯,ml)↦(ψn,1(m1),⋯,ψn,l(ml))
简记 A p = C R T p ( A p ) \mathbb A_p=CRT_p(A_p) Ap=CRTp(Ap),其中 A p A_p Ap 是 l l l 维向量空间,令 e ⃗ i ∈ A p \vec e_i \in A_p ei∈Ap 是单位向量,再令 π i = C R T p ( e ⃗ i ) \pi_i=CRT_p(\vec e_i) πi=CRTp(ei) 是对应的环元素。易知, π i ⋅ C R T p ( m ⃗ ) = C R T p ( 0 , ⋯ , m i , ⋯ , 0 ) \pi_i \cdot CRT_p(\vec m) = CRT_p(0,\cdots,m_i,\cdots,0) πi⋅CRTp(m)=CRTp(0,⋯,mi,⋯,0),于是 π i \pi_i πi 定义了投影映射。它可做为掩码,构造 Select 函数。
Slot Rotation
域自同构映射 κ j ∈ G a l ( K / Q ) \kappa_j \in Gal(K/\mathbb Q) κj∈Gal(K/Q),作用在整环 A p \mathbb A_p Ap 或者线性空间 A p A_p Ap 上(注意它们不是有限域),容易验证
κ j ( x ) ( m o d F i ) = κ j ( x ( m o d F i ) ) κ j ( C R T p ( x ⃗ ) ) = C R T p ( ⋯ , κ j ( x ( m o d F i ) ) , ⋯ ) \kappa_j(x) \pmod{F_i} = \kappa_j(x \pmod{F_i})\\ \kappa_j(CRT_p(\vec x)) = CRT_p(\cdots,\kappa_j(x \pmod{F_i}),\cdots) κj(x)(modFi)=κj(x(modFi))κj(CRTp(x))=CRTp(⋯,κj(x(modFi)),⋯)
因此 κ j \kappa_j κj 相对于 C R T p CRT_p CRTp 是可交换的。
由于整环 A p \mathbb A_p Ap 分解为 l = N / d l=N/d l=N/d 个有限域 G F ( p d ) GF(p^d) GF(pd) 的直积,因此 G a l ( K / Q ) Gal(K/\mathbb Q) Gal(K/Q) 包含循环子群 G = ( κ p ) \mathcal G=(\kappa_p) G=(κp),生成元是 Frobenius 映射 κ p : x ↦ x p \kappa_p:x \mapsto x^p κp:x↦xp。群 G \mathcal G G 是 p p p 的分解群。
定义商群 H = Z m ∗ / G \mathcal H = \mathbb Z_m^*/\mathcal G H=Zm∗/G,易知 o r d ( H ) = N / d = l ord(\mathcal H)=N/d=l ord(H)=N/d=l,且 H \mathcal H H 是阿贝尔群。根据有限阿贝尔群结构定理,可以分解为若干循环群的直积: H ≅ ∏ i = 1 t Z n i \mathcal H \cong \prod_{i=1}^t\mathbb Z_{n_i} H≅∏i=1tZni,并且满足 n i ∣ n i + 1 n_i|n_{i+1} ni∣ni+1 以及 ∏ i n i = l \prod_i n_i=l ∏ini=l,这些 n i n_i ni 称为不变因子。令 h i h_i hi 是循环群 Z n i \mathbb Z_{n_i} Zni 的陪集代表,那么 h = ∏ i = 1 t h i e i , 0 ≤ e i ≤ n i h=\prod_{i=1}^t h_i^{e_i},0 \le e_i \le n_i h=∏i=1thiei,0≤ei≤ni 就是全部的 H \mathcal H H 中陪集代表。
由于 ϕ m ( x ) = ∏ i F i ( x ) ( m o d p ) \phi_m(x)=\prod_i F_i(x) \pmod p ϕm(x)=∏iFi(x)(modp),我们将 ϕ m ( x ) \phi_m(x) ϕm(x) 的 ϕ ( m ) \phi(m) ϕ(m) 个根 { ζ m j : j ∈ Z m ∗ } \{\zeta_m^j: j \in \mathbb Z_m^*\} {ζmj:j∈Zm∗},根据素因子 F i F_i Fi 把根划分到 l = N / d l=N/d l=N/d 个集合中,集合 X i = { ( ζ m i ) p r : 1 ≤ r ≤ d } X_i=\{(\zeta_m^i)^{p^r}:1 \le r \le d\} Xi={(ζmi)pr:1≤r≤d} 是 F i F_i Fi 所有的根,它们相互共轭。因为 H \mathcal H H 大小是 l l l,且它在 l l l 个集合 X i X_i Xi 之间做迁移,我们令 ζ m \zeta_m ζm 是集合 X 1 X_1 X1 的代表,那么恰好存在唯一的 κ i ∈ H \kappa_i \in \mathcal H κi∈H 使得 κ i ( ζ m ) \kappa_i(\zeta_m) κi(ζm) 是集合 X i X_i Xi 的代表。
由于 κ j \kappa_j κj 和 C R T p CRT_p CRTp 交换,
- 循环群 G \mathcal G G 中的自同构 κ p \kappa_p κp,作用在槽 Z p [ x ] / ( F i ( x ) ) \mathbb Z_p[x]/(F_i(x)) Zp[x]/(Fi(x)) 上,执行了 X i X_i Xi 内部的单环置换,它对各个槽分别执行 Frobenius 映射,各个槽之间并没有置换
- 商群 H \mathcal H H 的代表元 κ k , k = i − 1 j \kappa_k, k=i^{-1}j κk,k=i−1j,作用在槽 Z p [ x ] / ( F i ( x ) ) \mathbb Z_p[x]/(F_i(x)) Zp[x]/(Fi(x)) 上,它将 ζ m i ∈ X i \zeta_m^i \in X_i ζmi∈Xi 映射到了 ζ m j ∈ X j \zeta_m^{j} \in X_{j} ζmj∈Xj,于是它可以实现任意两个槽之间的置换(但整体上不一定是单环置换)
- 对于某些特定的参数设置(比如 m = 2 N + 1 m=2^{N+1} m=2N+1 并且 m ∣ p − 1 m|p-1 m∣p−1),此时 H = { i d } \mathcal H=\{id\} H={id},并且 G \mathcal G G 恰好是某个单环置换(single cycle)生成的循环群,这就是 BGV 的 Slot Rotation 技术。
我们说对称群子群 H ⊂ S l H \subset S_l H⊂Sl 是快速迁移的(sharply transitive),如果对于任意的 i , j ∈ [ l ] i,j \in [l] i,j∈[l],都存在唯一的 h ∈ H h \in H h∈H 使得 h ( i ) = j h(i)=j h(i)=j 成立。易知,单环置换的循环群是快速迁移的;容易证明,商群 H \mathcal H H 也是快速迁移的。
Permutaion Network
BGV 的 SIMD 技术中,提供了 component-wise l l l-Add and l l l-Mult,以及底层代数结构提供的 l l l 个简单的快速迁移置换。我们希望再实现任意的 l l l-Permute,从而获得数组运算的完备集(complete set of operations for arrays)
在第 i − 1 i-1 i−1 层的输出线有 w w w 条,打包在大约 w / l w/l w/l 个密文中(可能包含 empty slots)。第 i i i 层的输入线有 w ′ w' w′ 条,它们是来自上一层输出线的任意映射:不一定是置换,有着不同的扇出系数,并且跨越密文做所有槽的大置换。[GHS12] 首先将各个槽扩增到扇出系数,然后使用置换网络对高维立方做置换:
- 第 i − 1 i-1 i−1 层的输出线是 w / l w/l w/l 个密文(虽然不知道 slot 的内容,但是知道 slot 对应的线),利用 Cloning 过程获得 k k k 个密文,它们包含了正确数量的输入线(但是槽的位置还没对应到第 i i i 层的输入线)
- 在 k × l k \times l k×l 的二维数组上,执行所需的置换,分为三个置换 π = π 3 ∘ π 2 ∘ π 1 \pi=\pi_3 \circ \pi_2 \circ \pi_1 π=π3∘π2∘π1,其中 π 2 \pi_2 π2 是对各行的单个 SIMD 密文做 l l l-Permute(使用 Shift Network),而 π 1 , π 3 \pi_1,\pi_3 π1,π3 是对各列的相同槽(域的模 F i F_i Fi 相同)做 t t t-Permute(使用 Select 和 Swap)
Hyper-Rectangles
令集合 S = [ n 1 ] × ⋯ × [ n k ] S=[n_1] \times \cdots \times [n_k] S=[n1]×⋯×[nk] 是高维立方的索引集合,每个元素是 k k k-维向量。那么 S S S 上任意的置换 π \pi π,可以写成 π = π 2 k − 1 ∘ ⋯ ∘ π k ∘ ⋯ ∘ π 1 \pi = \pi_{2k-1} \circ \cdots \circ \pi_{k} \circ \cdots \circ \pi_1 π=π2k−1∘⋯∘πk∘⋯∘π1,其中 π i , ∀ i ≤ k \pi_i,\forall i \le k πi,∀i≤k 只对第 i i i 个坐标作用,而 π i , ∀ i > k \pi_i,\forall i>k πi,∀i>k 只对第 2 k − i 2k-i 2k−i 个坐标作用。特别地,对于二维数组,可以写成 π = π 3 ∘ π 2 ∘ π 1 \pi=\pi_3 \circ \pi_2 \circ \pi_1 π=π3∘π2∘π1,其中 π 1 , π 3 \pi_1,\pi_3 π1,π3 作用在各列,而 π 2 \pi_2 π2 作用在各行。
- 对于二维数组 S = [ a ] × [ b ] S=[a] \times [b] S=[a]×[b],我们将 s ∈ S s \in S s∈S 记为 ( s x , s y ) (s_x,s_y) (sx,sy),其中 x x x 是行坐标, y y y 是列坐标。
- 我们让 π 1 \pi_1 π1 对每一列置换,使得重排后数组的每一行所有元素,其目标位置的 y y y 坐标 π y ( s i ) \pi_y(s_i) πy(si) 各不相同。接下来让 π 2 \pi_2 π2 对每一行做置换,把它们映射到目标位置对应的 y y y 坐标。最后让 π 3 \pi_3 π3 对每一列做置换,把它们映射到目标位置对应的 x x x 坐标。
- 我们根据置换 π \pi π 构造二部图 G = ( V 1 , V 2 , E ) G=(V_1,V_2,E) G=(V1,V2,E),其中 ∣ V 1 ∣ = ∣ V 2 ∣ = b |V_1|=|V_2|=b ∣V1∣=∣V2∣=b(坐标 y y y)。对于全部的 s ∈ S s \in S s∈S,在 V 1 V_1 V1 的点 s y s_y sy 到 V 2 V_2 V2 的点 π y ( s ) \pi_y(s) πy(s) 有边。易知,这个二部图是 a a a-正则的(regular),因此可以切分成 a a a 个完美匹配(perfect matches):所有点都是匹配点,所有边没有公共点。可使用匈牙利算法、KM算法来求解二部图的最大匹配。
- 我们对 G G G 的边染色 [ a ] [a] [a],使得完美匹配 G i G_i Gi 的颜色是 i i i,令 ρ ( s ) \rho(s) ρ(s) 表示边 s s s 的颜色,那么
- π 1 ( s ) = ( ρ ( s ) , s y ) \pi_1(s) = (\rho(s),s_y) π1(s)=(ρ(s),sy),置换 π 1 \pi_1 π1 将 x x x 坐标做置换,而 y y y 坐标不动,于是每列的 a a a 个元素被划分到了 a a a 个完美匹配中;
- π 2 ∘ π 1 ( s ) = ( ρ ( s ) , π y ( s ) ) \pi_2 \circ \pi_1(s) = (\rho(s),\pi_y(s)) π2∘π1(s)=(ρ(s),πy(s)),置换 π 2 \pi_2 π2 将 y y y 坐标映射到目标,而 x x x 坐标不动,它将第 ρ ( s ) \rho(s) ρ(s) 行的元素按照完美匹配 G ρ ( s ) G_{\rho(s)} Gρ(s) 做置换;
- π 3 ∘ π 2 ∘ π 1 ( s ) = ( π x ( s ) , π y ( s ) ) \pi_3 \circ\pi_2 \circ \pi_1(s) = (\pi_x(s),\pi_y(s)) π3∘π2∘π1(s)=(πx(s),πy(s)),置换 π 3 \pi_3 π3 将 x x x 坐标映射到目标,而 y y y 坐标不动,它用于纠正目标 x x x 坐标。
- 对于高维立方,递归调用二维数组的置换分解过程。
现在的问题是,如何实现一维数组上的置换,尤其是仅利用一些基本的置换(移位、旋转)组合出任意置换。[GHS12] 使用了 Benes 网络(大小受限为二的幂次),[HS14] 给出了更快速的推广版本。
Cloning
每个密文中打包了一些明文,标记各个槽为 “full” 或者 “empty”。我们称密文是稀疏的(sparse),如果两个密文中包含的 “empty” 数量超过 l l l,此时可以把两个密文 merge 到单个密文中。
输入 v 1 , ⋯ , v w v_1,\cdots,v_w v1,⋯,vw 的打包密文(大小约为 w / l w/l w/l 的密文数组 A A A),同时输入对应的扇出系数 m 1 , ⋯ , m w m_1,\cdots,m_w m1,⋯,mw(允许取 0 0 0),令 M = log ( max i m i ) M=\log(\max_i m_i) M=log(maximi)
- 初始化 A 0 = A A_0=A A0=A,然后将 m i = 0 m_i=0 mi=0 的那些槽标记上 empty,如果存在稀疏的两个密文,那么合并它们
- Decomposition:对于 i = 1 , ⋯ , M i=1,\cdots,M i=1,⋯,M,设置 A i = A i − 1 A_i=A_{i-1} Ai=Ai−1,并将 m i < 2 i m_i < 2^i mi<2i 的那些槽标记上 empty(并非设置 v i = 0 v_i=0 vi=0,需另外存储),如果存在稀疏的两个密文,那么合并它们
- Aggregation:设置 A M ′ = A M A_M'=A_M AM′=AM,对于 i = M − 1 , ⋯ , 0 i=M-1,\cdots,0 i=M−1,⋯,0,将数组 A i + 1 ′ ∥ A i + 1 ′ ∥ A i A_{i+1}'\|A_{i+1}'\|A_i Ai+1′∥Ai+1′∥Ai 作为 A i ′ A_i' Ai′(类似于快速幂),如果存在稀疏的两个密文,那么合并它们
- 最终输出 A 0 ′ A_0' A0′,它恰好包含了 m i m_i mi 个值 v i v_i vi,且数组中的 k k k 个密文是密集的
接下来,我们讨论如何在 k k k 个密文的全部 k ⋅ l k \cdot l k⋅l 个槽之间执行任意置换,将 clone 得到的数据放置到正确的位置上。
Batch Selection
为了实现 π 1 , π 3 \pi_1,\pi_3 π1,π3,我们使用 Benes/Waksman Network(two back-to-back butterfly network),实现一维数组上的任意置换:指标集 I = [ 2 r ] I=[2^r] I=[2r](表示为 r r r 比特数),网络包含 2 r − 1 2r-1 2r−1 层,每一层有 2 r 2^r 2r 个节点;第 i − 1 i-1 i−1 层和第 i i i 层之间的边只有两种情况:一对指标 j , j ′ j,j' j,j′,它们只有第 k = ∣ r − i ∣ k=|r-i| k=∣r−i∣ 比特不同,即 j ′ = j + 2 k j'=j+2^{k} j′=j+2k,共有 2 r − 1 2^{r-1} 2r−1 对指标,
- straight edge:每一对 j , j ′ j,j' j,j′,第 i − 1 i-1 i−1 层的 j j j 连接到第 i i i 层的 j j j,第 i − 1 i-1 i−1 层的 j ′ j' j′ 连接到第 i i i 层的 j ′ j' j′
- cross edge:每一对 j , j ′ j,j' j,j′,第 i − 1 i-1 i−1 层的 j j j 连接到第 i i i 层的 j ′ j' j′,第 i − 1 i-1 i−1 层的 j ′ j' j′ 连接到第 i i i 层的 j j j
Benes Network:集合 I = [ 2 r ] I=[2^r] I=[2r] 上的任意置换 π \pi π,给出了 r r r 维 Benes 网络上的一组不交路径(node-disjoint path),使得 i → P i π ( i ) , ∀ i i \overset{P_i}{\to} \pi(i),\forall i i→Piπ(i),∀i 成立。换句话说,相邻层之间的每一对指标 j , j ′ j,j' j,j′,它们要么不交换(直边)、要么交换(叉边),可通过使用 control bit 控制 Switch Gate 来实现。
给定两个密文 A 0 = [ m 1 ( 0 ) , ⋯ , m l ( 0 ) ] A_0=[m_1^{(0)},\cdots,m_l^{(0)}] A0=[m1(0),⋯,ml(0)] 和 A 1 = [ m 1 ( 1 ) , ⋯ , m l ( 1 ) ] A_1=[m_1^{(1)},\cdots,m_l^{(1)}] A1=[m1(1),⋯,ml(1)],再令 S = [ s 1 , ⋯ , s l ] ∈ { 0 , 1 } l S=[s_1,\cdots,s_l] \in \{0,1\}^l S=[s1,⋯,sl]∈{0,1}l 是掩码,那么
S e l e c t S ( A 0 , A 1 ) = A d d ( M u l t ( A , S ˉ ) , M u l t ( A ′ , S ) ) Select_S(A_0,A_1) = Add(Mult(A,\bar S),\,\, Mult(A',S)) SelectS(A0,A1)=Add(Mult(A,Sˉ),Mult(A′,S))
得到密文 [ m 1 ( s 1 ) , ⋯ , m l ( s l ) ] [m_1^{(s_1)},\cdots,m_l^{(s_l)}] [m1(s1),⋯,ml(sl)],它根据 S S S 挑选 A 0 , A 1 A_0,A_1 A0,A1 的元素。进一步的,计算
S w i t c h S ( A 0 , A 1 ) = ( S e l e c t S ( A 0 , A 1 ) , S e l e c t S ˉ ( A 0 , A 1 ) ) Switch_S(A_0,A_1) = \left(Select_S(A_0,A_1),\,\, Select_{\bar S}(A_0,A_1)\right) SwitchS(A0,A1)=(SelectS(A0,A1),SelectSˉ(A0,A1))
那么 s i = 0 s_i=0 si=0 的那些位置不发生交换,而 s i = 1 s_i=1 si=1 的那些位置发生了交换。
对于 k × l k \times l k×l 的二维数组上的 π 1 , π 3 \pi_1,\pi_3 π1,π3 对于各个列分别置换,假设 k = 2 r k=2^r k=2r(通过填充),那么可以构建 r r r 维的 Benes 网络,为第 i − 1 i-1 i−1 层和第 i i i 层之间的 Switch Gate 设置 S j , j ′ S_{j,j'} Sj,j′,执行并行的(但是 control bit 独立)交换电路。Benes 网络的深度 2 r − 1 = O ( log k ) 2r-1=O(\log k) 2r−1=O(logk),交换节点的数量 k ( 2 r − 1 ) / 2 = O ( k log k ) k(2r-1)/2=O(k\log k) k(2r−1)/2=O(klogk),复杂度是 ploylog 的。
Shift Network
剩下的问题就是如何使用底层代数结构所给于的置换子集 H ⊆ G a l ( Q ( ζ m ) / Q ) \mathcal H \subseteq Gal(\mathbb Q(\zeta_m)/\mathbb Q) H⊆Gal(Q(ζm)/Q),实现单个密文上 l = N / d l=N/d l=N/d 个槽的任意置换。
对于特殊参数设置,商群 H \mathcal H H 中的元素作用在密文上导致了 slot rotation(单环置换)。我们假设循环群生成元是 σ \sigma σ,经过对槽的合理排序,映射 σ k \sigma^k σk 将 ( m 1 , ⋯ , m l ) (m_1,\cdots,m_l) (m1,⋯,ml) 映射为 ( m k , ⋯ , m l , m 1 , ⋯ , m k − 1 ) (m_k,\cdots,m_l,m_1,\cdots,m_{k-1}) (mk,⋯,ml,m1,⋯,mk−1),是个循环移位。
我们称 I = [ l ] I=[l] I=[l] 上的映射 π \pi π 是 i i i-offset swap,如果 π \pi π 可以分解为 1 1 1-cycles 和 2 2 2-cycles,并且这些 2 2 2-cycles 都形如 ( k , k + i ) ( m o d l ) (k,k+i) \pmod l (k,k+i)(modl)。那么,任意的 i i i-offset swap 可以通过两个 Batch Select,然后分别使用 σ i \sigma^i σi 和 σ l − i \sigma^{l-i} σl−i 旋转对应的槽,最后加起来即可。令 r = log l r=\log l r=logl,在 Benes 网络中只需要形如 ( j , j + 2 ∣ r − i ∣ ) ( m o d 2 r ) (j,j+2^{|r-i|}) \pmod{2^r} (j,j+2∣r−i∣)(mod2r) 的置换,因此使用 O ( log l ) O(\log l) O(logl) 个槽旋转即可完成任意置换。
然而,对于一般的参数设置, H \mathcal H H 仅仅是一个 Sharply Transitive Permutation Groups,不一定是由循环移位组成的循环群。将有限阿贝尔群写作循环群直积
H ≅ ∏ i = 1 k Z n i , ∀ i , n i ∣ n i + 1 , ∏ i n i = l \mathcal H \cong \prod_{i=1}^k\mathbb Z_{n_i},\,\, \forall i,n_i|n_{i+1},\,\, \prod_i n_i=l H≅i=1∏kZni,∀i,ni∣ni+1,i∏ni=l
于是元素 h ∈ H h \in \mathcal H h∈H 可以记为盒子 B = ∏ i = 1 k Z n i \mathcal B=\prod_{i=1}^k\mathbb Z_{n_i} B=∏i=1kZni 中的向量 h ⃗ \vec h h,群元素运算就等价于向量的加法。令 { e r } r = 1 t \{e_r\}_{r=1}^t {er}r=1t 是单位向量,易知它是 H \mathcal H H 的生成集。
因为 H \mathcal H H 是集合 I = [ l ] I=[l] I=[l] 上的快速迁移,我们固定某个索引 i 0 ∈ I i_0 \in I i0∈I(例如 i 0 = 1 i_0=1 i0=1),那么我们遍历 h ∈ H h \in \mathcal H h∈H(此时 h ( i 0 ) h(i_0) h(i0) 遍历 I I I),对每个 h ( i 0 ) h(i_0) h(i0) 标记上 h ⃗ \vec h h,这就把一维数组 I I I 转化为了高阶立方 B \mathcal B B
生成元 e r ∈ H e_r \in \mathcal H er∈H 作用在指标 i i i 上,假如 i = h ∗ ( i 0 ) i=h^*(i_0) i=h∗(i0), 那么得到
e r ( i ) = e r ( h ∗ ( i 0 ) ) = ( e r h ∗ ) ( i 0 ) e_r(i) = e_r(h^*(i_0)) = (e_r h^*)(i_0) er(i)=er(h∗(i0))=(erh∗)(i0)
于是 e r ( i ) e_r(i) er(i) 的标签是 e ⃗ r + h ⃗ ∗ ( m o d B ) \vec e_r+\vec h^* \pmod{\mathcal B} er+h∗(modB),这就是对第 r r r 个坐标执行了 ( m o d n r ) \pmod{n_r} (modnr) 的循环移位。因此,我们将 I I I 视为 t t t 阶立方 B \mathcal B B,
- 指标集 I = [ l ] ≅ B I=[l] \cong \mathcal B I=[l]≅B 上的任意置换 π \pi π,分解为 π = π 2 k − 1 ∘ ⋯ ∘ π 1 \pi = \pi_{2k-1} \circ \cdots \circ \pi_1 π=π2k−1∘⋯∘π1,其中的 π i , ∀ i ≤ k \pi_i,\forall i \le k πi,∀i≤k 只对第 i i i 个坐标做置换,而 π i , ∀ i > k \pi_i,\forall i>k πi,∀i>k 只对第 2 k − i 2k-i 2k−i 个坐标做置换
- 对于 i ≤ k i \le k i≤k,集合 [ n i ] [n_i] [ni] 上的置换 π i \pi_i πi,使用循环子群 ( e i ) (e_i) (ei) 构造 offset swap,构建 Benes 网络来实现 π i \pi_i πi(并行的 l / n i l/n_i l/ni 个网络,使用不同的 select bit 并行处理)
- 对于 i > k i > k i>k,集合 [ n 2 k − i ] [n_{2k-i}] [n2k−i] 上的置换 π i \pi_i πi,使用循环子群 ( e 2 k − i ) (e_{2k-i}) (e2k−i) 构造 offset swap,构建 Benes 网络来实现 π i \pi_i πi(并行的 l / n i l/n_i l/ni 个网络,使用不同的 select bit 并行处理)
- 将上述的 2 k − 1 2k-1 2k−1 组 Benes 网络串联起来,就实现了 π \pi π 置换
这个由 Benes 网络组合出来的置换网络,它的深度为 O ( log l ) O(\log l) O(logl),每层的 Rotate 和 Select 数量都是常数。
Shift-Networks
[HS14] 给出了移位网络的定义。对于 I = [ l ] I=[l] I=[l] 上的置换 π \pi π,移位列(shift-column) s h π [ i ] = π ( i ) − i ∈ [ − l + 1 , l − 1 ] sh_\pi[i]=\pi(i)-i \in [-l+1,l-1] shπ[i]=π(i)−i∈[−l+1,l−1] 是记录置换导致移动距离的列向量,令 m δ ∈ { 0 , 1 } l m_\delta \in \{0,1\}^l mδ∈{0,1}l 是那些 s h π [ i ] = δ sh_\pi[i]=\delta shπ[i]=δ 的掩码,那么 w = ∑ δ ∈ s h π ( m δ × v ) ≫ δ w = \sum_{\delta \in sh_\pi} (m_\delta \times v) \gg \delta w=∑δ∈shπ(mδ×v)≫δ,其中 × \times × 是阿达玛乘积, ≫ \gg ≫ 是移位。我们定义开销(cost)是 s h π sh_\pi shπ 中出现的不同的非零值的个数。移位网络(Shift Network)是 l × d l \times d l×d 形状的矩阵,网络深度为 d d d,它的每一列都是移位列,代表了 π 1 , ⋯ , π d \pi_1,\cdots,\pi_d π1,⋯,πd,网络对应的置换是 π = π d ∘ ⋯ ∘ π 1 \pi=\pi_d \circ \cdots \circ \pi_1 π=πd∘⋯∘π1。网络开销是所有移位列开销的加和。
Cheapest-shift-network Problem:给定 [ n ] [n] [n] 上的置换 π \pi π,以及深度上界 B B B,尝试给出一个深度至多为 B B B 的移位网络,使得网络开销最小化。易知,大多数置换拥有 cost- Ω ( n ) \Omega(n) Ω(n) depth- 1 1 1 的移位网络,全部的置换都有 cost- O ( n ) O(\sqrt n) O(n) depth-2 移位网络,以及 cost- O ( d ⋅ n 1 / d ) O(d \cdot n^{1/d}) O(d⋅n1/d) depth- d d d 的移位网络。
求解 CSN 被认为是困难的,但是足够给出一类足够优秀的网络:Benes Networks。设 n = 2 r n=2^r n=2r,它的深度为 2 r − 1 = O ( log n ) 2r-1=O(\log n) 2r−1=O(logn),开销是 4 r − 2 = O ( log n ) 4r-2=O(\log n) 4r−2=O(logn)。它被应用于交换机、电话交换网络。
Benes Network
[GHS12] 中使用 Benes 网络分别实现了 π 1 , π 2 , π 3 \pi_1,\pi_2,\pi_3 π1,π2,π3,但是文中没有给出 Benes 网络的具体构造方法。[HS14] 给出了方法。
给定 S = [ n ] , n = 2 r S=[n],n=2^r S=[n],n=2r 上的任意置换 π \pi π,将它分解为
π = σ r − 1 ∘ ⋯ ∘ σ 1 ∘ σ 0 ∘ τ 1 ∘ ⋯ ∘ τ r − 1 \pi = \sigma_{r-1} \circ \cdots \circ \sigma_1 \circ \sigma_0 \circ \tau_1 \circ \cdots \circ \tau_{r-1} π=σr−1∘⋯∘σ1∘σ0∘τ1∘⋯∘τr−1
其中 σ k , τ k \sigma_k, \tau_k σk,τk 把元素 i ∈ [ n ] i \in [n] i∈[n] 映射到三种可能: i , i + 2 k , i − 2 k i,i+2^k,i-2^k i,i+2k,i−2k
采用递归算法:
-
令 m = n / 2 = 2 r − 1 m=n/2=2^{r-1} m=n/2=2r−1,我们把 S S S 分为上下两部分, S 0 = [ 0 , ⋯ , m − 1 ] S_0=[0,\cdots,m-1] S0=[0,⋯,m−1], S 1 = [ m , ⋯ , n − 1 ] S_1=[m,\cdots,n-1] S1=[m,⋯,n−1]
-
做分解 π = σ ∘ ρ ∘ τ \pi=\sigma \circ \rho \circ \tau π=σ∘ρ∘τ,使得
- σ , τ \sigma,\tau σ,τ 将 i ∈ S 0 i \in S_0 i∈S0 映射到 i ∈ S 0 i \in S_0 i∈S0 或者 i + m ∈ S 1 i+m \in S_1 i+m∈S1,将 i ∈ S 1 i \in S_1 i∈S1 映射到 i ∈ S 1 i \in S_1 i∈S1 或者 i − m ∈ S 0 i-m \in S_0 i−m∈S0
- ρ \rho ρ 包含两个置换 π 0 , π 1 \pi_0,\pi_1 π0,π1,它们分别对子集 S 0 , S 1 S_0,S_1 S0,S1 做置换
-
构造二部图 G = ( L , R , E ) G=(L,R,E) G=(L,R,E),其中 ∣ L ∣ = ∣ R ∣ = n |L|=|R|=n ∣L∣=∣R∣=n,
- permutation edge:根据 π \pi π,在 L i L_i Li 和 R π ( i ) R_{\pi(i)} Rπ(i) 之间添加边(形成了一个完美匹配)
- conflict edge:在 L i L_i Li 和 L i + m L_{i+m} Li+m 之间添加边,在 R i R_i Ri 和 R i + m R_{i+m} Ri+m 之间添加边
容易看出 E E E 组成了汉密尔顿回路,并且 ( L , R ) (L,R) (L,R) 可以二染色(permutation edge 和 conflict edge 交替出现), C ( v ) ∈ { 0 , 1 } C(v) \in \{0,1\} C(v)∈{0,1}
-
根据点集 L L L 的染色情况,把它们分为上下两部分
- 如果 i ∈ S 0 i \in S_0 i∈S0 且 C ( L i ) = 0 C(L_i)=0 C(Li)=0,那么令 τ ( i ) = i ∈ S 0 \tau(i)=i \in S_0 τ(i)=i∈S0
- 如果 i ∈ S 1 i \in S_1 i∈S1 且 C ( L i ) = 1 C(L_i)=1 C(Li)=1,那么令 τ ( i ) = i ∈ S 1 \tau(i)=i \in S_1 τ(i)=i∈S1
- 如果 i ∈ S 0 i \in S_0 i∈S0 且 C ( L i ) = 1 C(L_i)=1 C(Li)=1,那么令 τ ( i ) = i + m ∈ S 1 \tau(i)=i+m \in S_1 τ(i)=i+m∈S1
- 如果 i ∈ S 1 i \in S_1 i∈S1 且 C ( L i ) = 0 C(L_i)=0 C(Li)=0,那么令 τ ( i ) = i − m ∈ S 0 \tau(i)=i-m \in S_0 τ(i)=i−m∈S0
于是 τ \tau τ 变换后, S 0 S_0 S0 中的点都是颜色 0 0 0, S 1 S_1 S1 中的点都是颜色 1 1 1,花费是 + m +m +m 和 − m -m −m 的两个 batch select + shift
-
根据点集 R R R 的染色情况,把它们分为上下两部分
- 如果 i ∈ S 0 i \in S_0 i∈S0 且 C ( R i ) = 0 C(R_i)=0 C(Ri)=0,那么令 σ − 1 ( i ) = i + m ∈ S 1 \sigma^{-1}(i)=i+m \in S_1 σ−1(i)=i+m∈S1
- 如果 i ∈ S 1 i \in S_1 i∈S1 且 C ( L i ) = 1 C(L_i)=1 C(Li)=1,那么令 σ − 1 ( i ) = i − m ∈ S 0 \sigma^{-1}(i)=i-m \in S_0 σ−1(i)=i−m∈S0
- 如果 i ∈ S 0 i \in S_0 i∈S0 且 C ( L i ) = 1 C(L_i)=1 C(Li)=1,那么令 σ − 1 ( i ) = i ∈ S 0 \sigma^{-1}(i)=i \in S_0 σ−1(i)=i∈S0
- 如果 i ∈ S 1 i \in S_1 i∈S1 且 C ( L i ) = 0 C(L_i)=0 C(Li)=0,那么令 σ − 1 ( i ) = i ∈ S 1 \sigma^{-1}(i)=i \in S_1 σ−1(i)=i∈S1
于是 σ − 1 \sigma^{-1} σ−1 变换后, S 0 S_0 S0 中的点都是颜色 1 1 1, S 1 S_1 S1 中的点都是颜色 0 0 0,花费是 + m +m +m 和 − m -m −m 的两个 batch select + shift
-
可以看出 τ ( L ) \tau(L) τ(L) 和 σ − 1 ( R ) \sigma^{-1}(R) σ−1(R) 将图 G G G 分为了两个二部图 G 0 , G 1 G_0,G_1 G0,G1,两个子图之间没有 permutation edge(仅在 S 0 S_0 S0 和 S 1 S_1 S1 内部分别置换),因此我们就得到了中间的置换 ρ = ( π 0 ) ( π 1 ) \rho=(\pi_0)(\pi_1) ρ=(π0)(π1),递归分解。
它是 “背靠背” 的两个蝴蝶网络:以 n = 2 3 n=2^3 n=23 为例,两个深度 3 3 3 的网络,
注意,上图画的有些问题(没找到更好的网图。。。):左上、右上的那两对节点,缺少了直边!
General Benes Network
[HS14] 给出了更加快速的 Benes 网络:假设 n n n 不是二的幂次,并非将它填充到 2 r 2^r 2r,而是将它分割为近似相等的两个子图。
-
如果 n n n 是偶数,那么 m = n / 2 m=n/2 m=n/2,于是 Benes 的分割流程是工作的
-
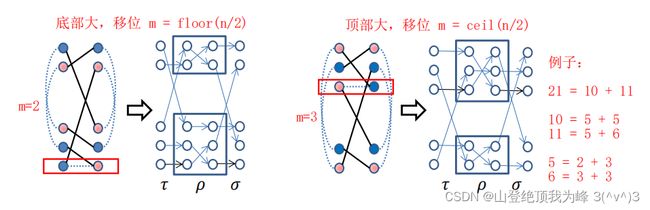
如果 n n n 是奇数,有两种设置: m = ( n − 1 ) / 2 m = (n-1)/2 m=(n−1)/2 或者 m = ( n + 1 ) / 2 m=(n+1)/2 m=(n+1)/2,我们令 S 0 = { 0 , ⋯ , m − 1 } S_0=\{0,\cdots,m-1\} S0={0,⋯,m−1}, S 1 = { m , ⋯ , n − 1 } S_1=\{m,\cdots,n-1\} S1={m,⋯,n−1},它们的大小差距为 1 1 1
-
为了保证分割后,同一个 level 中所有置换的移动距离相同,
- 大小 n n n 的图,移动距离 m = ⌊ n / 2 ⌉ m=\lfloor n/2 \rceil m=⌊n/2⌉,划分为大小 ( n − 1 ) / 2 (n-1)/2 (n−1)/2 以及 ( n + 1 ) / 2 (n+1)/2 (n+1)/2 的两个子图
- 对于这两个大小接近的子图,设置相同的移动距离 m ′ = ⌊ n / 4 ⌉ m'=\lfloor n/4 \rceil m′=⌊n/4⌉,划分为四个大小接近 n / 4 n/4 n/4 的子图
- 这些子图的大小差距也至多为 1 1 1,因此可以继续设置相同的偏移 m ′ ′ m'' m′′,划分出大小差距至多为 1 1 1 的多个子图
注意, ⌊ ( ( n − 1 ) / 2 ) / 2 ⌉ ≠ ⌊ ( ( n + 1 ) / 2 ) / 2 ⌉ \lfloor ((n-1)/2)/2 \rceil \neq \lfloor ((n+1)/2)/2 \rceil ⌊((n−1)/2)/2⌉=⌊((n+1)/2)/2⌉,因此上述的偏移 m ′ , m ′ ′ , ⋯ m',m'',\cdots m′,m′′,⋯ 并不是以子图本身大小来计算的!必须根据整个图的大小 n n n 以及分解的 level 层级来计算。
-
最终得到了深度 2 ⌈ log n ⌉ − 1 2\lceil \log n \rceil-1 2⌈logn⌉−1 的移位网络,同一层的移位距离都是 ⌊ n / 2 k ⌉ \lfloor n/2^k \rceil ⌊n/2k⌉,因此只需要两个 batch select + shift
两种 m m m 的选择, S 0 , S 1 S_0,S_1 S0,S1 的大小差距 1 1 1,因此制作 conflict edge 的时候,会有一个指标 i ∗ i^* i∗ 剩余,我们特别地设置它的 conflict edge 是自己到自己。对应的二染色,如图所示: