小白学习深度学习之（一）——线性回归

什么是回归

回归问题是能为一个或多个自变量与因变量之间关系建模的一类方法。在自然科学与社会科学领域，回归经常用来表示输入和输出之间的关系

在计算机视觉领域，大多数任务都和预测有关。当我们需要与预测一个数值时，就会涉及到回归问题。

线性模型

首先，假设自变量 和因变量 之间的关系是线性的， 即 可以表示为 中元素的加权和，这里通常允许包含观测值的一些噪声； 其次，我们假设任何噪声都比较正常，如噪声遵循正态分布。

线性模型基本形式：̂ =+

损失函数

在我们开始考虑如何用模型拟合（fit）数据之前，我们需要确定一个拟合程度的度量。 损失函数（loss function）能够量化目标的实际值与预测值之间的差距。 通常我们会选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为0。

回归问题中最常用的损失函数是平方误差函数。 当样本 的预测值为 ̂ () ，其相应的真实标签为 () 时， 平方误差可以定义为以下公式：$$l^{(i)}(\mathbf{w},b)=\frac{1}{2}{\left({\hat{y}}^{(i)}-y^{(i)}\right)}^2.$$

在训练模型时，我们希望寻找一组参数（${\mathbf{w}}^{\ast },b^{\ast }$），这组参数能最小化在所有训练样本上的总损失。如下式：

$${\mathbf{w}}^{\ast },b^{\ast }=\underset{\mathbf{w},b}{\mathrm{argmin}}L(\mathbf{w},b).$$

解析解

线性回归刚好是一个简单的优化问题，与我们将在本书中所讲到的其他大部分模型不同，线性回归的解可以用一个公式简单的表达出来，这类解叫作解析解。

随机梯度下降

即使在我们无法得到解析解的情况下，我们仍然可以有效地训练模型。 在许多任务上，那些难以优化的模型效果要更好。 因此，弄清楚如何训练这些难以优化的模型是非常重要的。

本书中我们用到一种名为梯度下降（gradient descent）的方法， 这种方法几乎可以优化所有深度学习模型。 它通过不断地在损失函数递减的方向上更新参数来降低误差。

梯度下降最简单的用法是计算损失函数（数据集中所有样本的损失均值） 关于模型参数的导数（在这里也可以称为梯度）。 但实际中的执行可能会非常慢：因为在每一次更新参数之前，我们必须遍历整个数据集。 因此，我们通常会在每次需要计算更新的时候随机抽取一小批样本， 这种变体叫做小批量随机梯度下降（minibatch stochastic gradient descent）。

矢量化加速

在训练我们的模型时，我们经常希望能够同时处理整个小批量的样本。为了实现这一点，需要我们对计算进行矢量化，从而利用线性代数库，而不是在python中编写开销高昂的for循环

从线性回归到深度网络

到目前为止，我们只谈论了线性模型。 尽管神经网络涵盖了更多更为丰富的模型，我们依然可以用描述神经网络的方式来描述线性模型， 从而把线性模型看作一个神经网络。 首先，我们用“层”符号来重写这个模型。

神经网络图

深度学习从业者喜欢绘制图表来可视化模型中正在发生的事情。在图中，我们将线性回归模型描述为一个神经网络

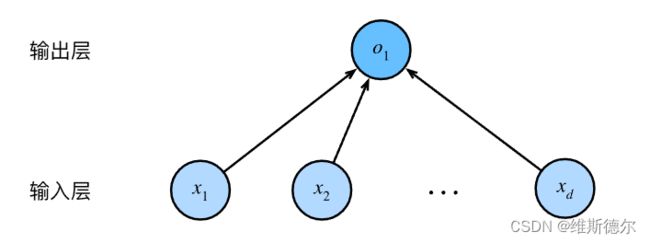
对于线性回归，每个输入都与每个输出（在本例中只有一个输出）相连， 我们将这种变换称为全连接层（fully-connected layer）或称为稠密层（dense layer）。

线性回归的简洁实现

在过去几年中，出于对深度学习的强烈的兴趣，许多公司，学者和业余爱好者开发了各种成熟的开源框架。这些框架可以自动化基于对梯度的学习算法中重复的工作。

生成数据集

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

读取数据集

我们可以**[调用框架中现有的API来读取数据]。 我们将features和labels作为API的参数传递，并通过数据迭代器指定batch_size**。 此外，布尔值is_train表示是否希望数据迭代器对象在每个迭代周期内打乱数据。

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)  #*的意思是将data_arrays变成一个可迭代对象
    return data.DataLoader(dataset, batch_size, shuffle=is_train)  #shuffle随即打乱

batch_size = 10
data_iter = load_array((features, labels), batch_size)
#next一个一个的输出，一项一项输出
next(iter(data_iter))

定义模型

对于标准深度学习模型，我们可以[使用框架的预定义好的层]。这使我们只需关注使用哪些层来构造模型，而不必关注层的实现细节。 我们首先定义一个模型变量net，它是一个Sequential类的实例。 Sequential类将多个层串联在一起。 当给定输入数据时，Sequential实例将数据传入到第一层， 然后将第一层的输出作为第二层的输入，以此类推。 在下面的例子中，我们的模型只包含一个层，因此实际上不需要Sequential。 但是由于以后几乎所有的模型都是多层的，在这里使用Sequential会让你熟悉“标准的流水线”。

# nn是神经网络的缩写
from torch import nn
net = nn.Sequential(nn.Linear(2, 1))

初始化模型参数

在使用net之前，我们需要初始化模型参数。 如在线性回归模型中的权重和偏置。 深度学习框架通常有预定义的方法来初始化参数。 在这里，我们指定每个权重参数应该从均值为0、标准差为0.01的正态分布中随机采样， 偏置参数将初始化为零。

正如我们在构造nn.Linear时指定输入和输出尺寸一样， 现在我们能直接访问参数以设定它们的初始值。 我们通过net[0]选择网络中的第一个图层， 然后使用weight.data和bias.data方法访问参数。 我们还可以使用替换方法normal_和fill_来重写参数值。

net[0].weight.data.normal_(0, 0.01) #填充一个正态分布
net[0].bias.data.fill_(0) #所有的填充0

定义损失函数

loss = nn.MSELoss()  #平方损失

定义优化算法

trainer = torch.optim.SGD(net.parameters(), lr=0.03)   #net.parameters()返回net网络中所有的参数

训练

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad()
        l.backward()
        trainer.step()  #模型的更新
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

运行结果
epoch 1, loss 0.000682
epoch 2, loss 0.000109
epoch 3, loss 0.000109

w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

运行结果
w的估计误差： tensor([-0.0010, -0.0003])
b的估计误差： tensor([-0.0003])