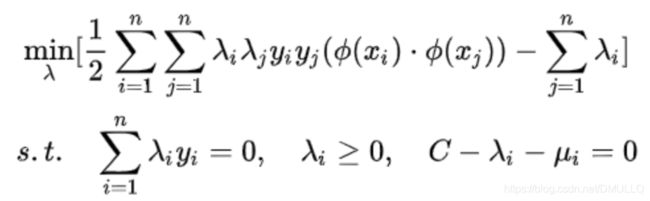机器学习-基于支持向量机的分类预测（基础概念）

支持向量机

• 支持向量机（Support Vector Machine, SVM）是一种对数据进行二分类的广义线性分类器，其分类边界是对学习样本求解的最大间隔超平面。

用我自己话说，就是一种二分类器，分类方式是画一个平面，这个平面到两边最近点点距离最大。看看下图来了解一下（图来自网络）：

这两条线都能划分清楚，但是要选一个最优的，评判标准是什么？间距越大越优秀，容错率越小嘛，就像就开车走马路中间最安全。
所以选择下面一条：

• 支持向量机的机制就是取最大margin的超平面。而支持向量是什么？上面几幅图中灰色边缘最近的点就是“支持向量”—大白话说就是 margin扩张扩到数据的边界了，贴近边界最近的数据点就是“支持向量”

超平面

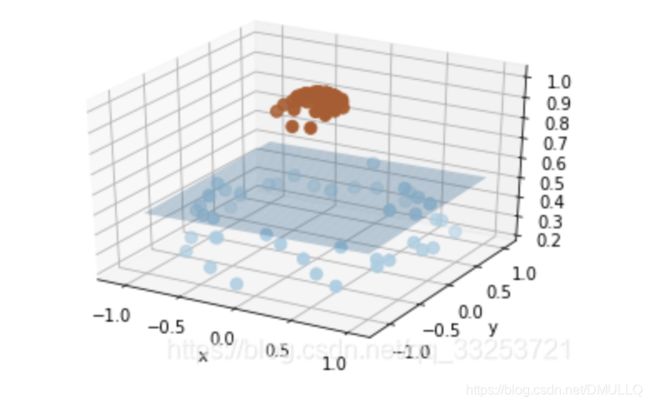
• 如果原数据是线性不可分的，就是不能通过画一条线（一个面）把数据集分开，如图：
  
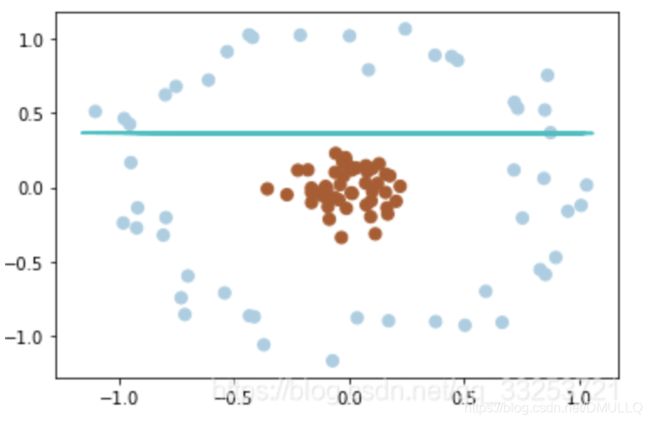
• 如果将二维（低维）空间的数据映射到三维（高维）空间中，便可以通过一个超平面对数据进行划分。
  所以，我们映射的目的在于使用 SVM 在高维空间找到超平面的能力。
  

分类线方程：

$$w\cdot x+b=0,w\in R^m,b\in R$$

• 分类间隔：
  $$M=\frac{2}{||w||}$$

这个公式怎么来的，有一个退到过程，这里引用一个别人的《推导过程》，通过让w取最小值来获得最优超平面

• 这里点约束条件：
  $$y_i(w{x}_i+b)-1⩾0i=1,\dots ,n$$

约束条件是什么？这个需要进一步探讨……

• 所以求最大间隔问题成了约束优化问题：
  $$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2-\sum _{i=1}^m{\alpha }_i(y_i(w\cdot x_i+b)-1)$$

用拉格朗日方法求解。其中，${\alpha }_i⩾0$为每一个样本的拉氏乘子 ，由L分别对b和w导数为0.可以导出：$\sum _{i=1}^m{\alpha }_i{y}_i=0w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i$

核函数

• 我们知道对于线性不可分的样本点需要映射到高维空间，用 x 表示原来的样本点，用 φ(x)表示 x 映射到特征新的特征空间后到新向量。那么分割超平面可以表示为：
  $$f(x)=w\varphi (x)+b$$

• 对于非线性SVM问题就变成了：
  

• 就是把低维度的$(x_i\cdot y_j)$变成了高维度的$(\varphi (x_i)\cdot \varphi (y_j))$问题。

核函数的作用

• 低维空间映射到高维空间后维度可能会很大，如果将全部样本的点乘全部计算好，这样的计算量太大了。但如果我们有这样的一核函数 ：
  $$k(x,y)=(\varphi (x),\varphi (y))$$
  xi与xj在特征空间的内积等于它们在原始样本空间中通过函数 k(x,y) 计算的结果，就不需要计算高维甚至无穷维空间的内积了.假设一个多项式核函数：
  $$k(x,y)=(x\cdot y+1{)}^2$$
  带入样本点后：
  $$k(x,y)=(\sum _{i=1}^n(x_i,y_i)+1{)}^2$$
  拉式展开：
  $$\sum _{i=1}^n{x}_i^2{y}_i^2+\sum _{i=2}^n\sum _{j=1}^{i-1}(\sqrt{2}{x}_i{x}_j)(\sqrt{2}{y}_i{x}_j)+\sum _{i=1}^{n}n(\sqrt{2}{x}_i)(\sqrt{2}{y}_i)+1$$
  如没有核函数，我们则需要把向量映射成：
  $$x^{{}^{\prime }}=(x_1^2,\dots ,x_n^2,\dots ,\sqrt{2}{x}_1,\dots ,\sqrt{2}{x}_n,1)$$
  然后再进行内积计算，才能与多项式核函数达到相同的效果。
  可见核函数的引入一方面减少了我们计算量，另一方面也减少了我们存储数据的内存使用量。

常见的核函数

• 线性核函数
  $$k(x_i,x_j)=x_i^T{x}_j$$
• 多项式核函数
  $$k(x_i,x_j)=(x_i^T{x}_j{)}^d$$
• 高斯核函数(需要调参)
  $$k(x_i,x_j)=exp(-\frac{||x_i-x_j||}{2{\delta }^2})$$

案例

• 导入数据集

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
%matplotlib inline
# 画图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=60, cmap=plt.cm.Paired)

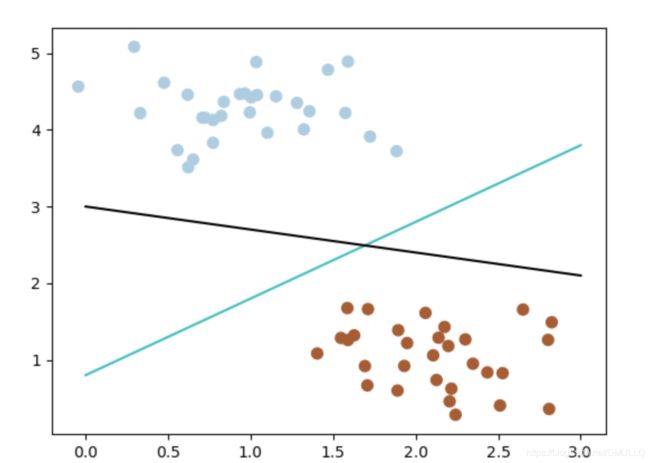
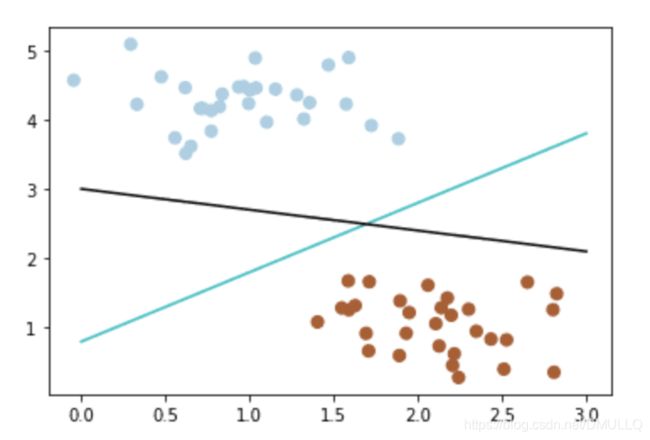
• 线性负分类器（有多种）

# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
x_fit = np.linspace(0, 3)
# 画函数
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
y_2 = -0.3 * x_fit + 3
plt.plot(x_fit, y_2, '-k')

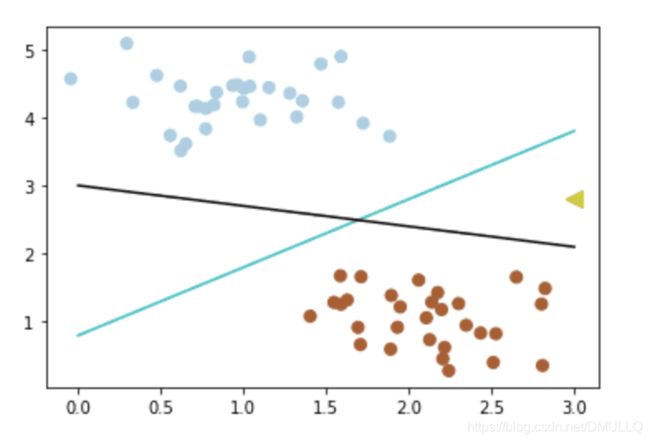
• 不确定哪个更好，不妨新加入一个新数据（3，2.8）

# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
plt.scatter([3], [2.8], c='#cccc00', marker='<', s=100, cmap=plt.cm.Paired)
x_fit = np.linspace(0, 3)
# 画函数
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
y_2 = -0.3 * x_fit + 3
plt.plot(x_fit, y_2, '-k')

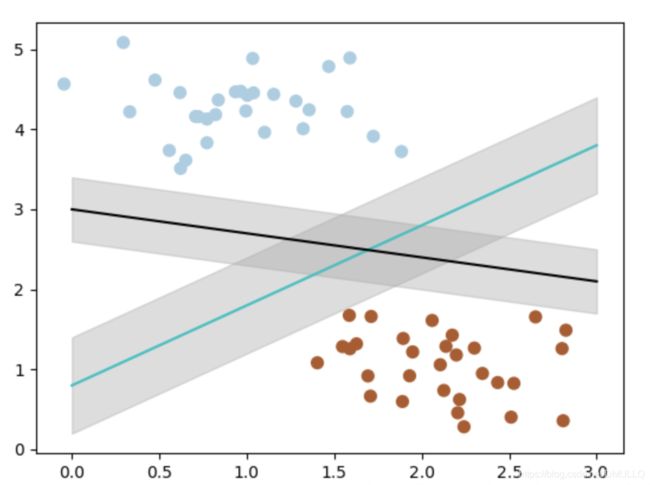
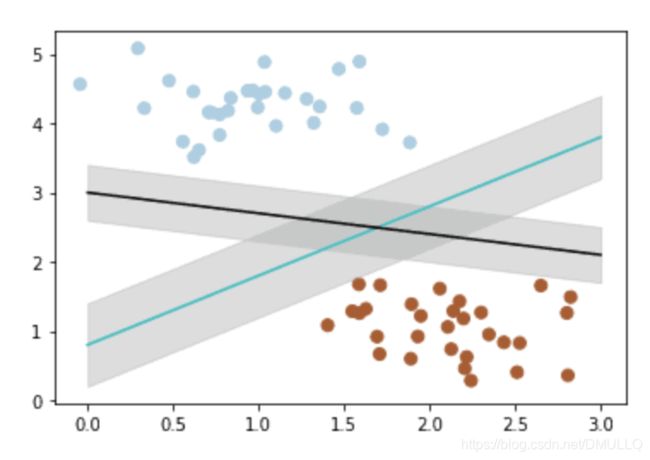
• 那么如何客观的评判两条线的健壮性呢？ 此时，我们需要引入一个非常重要的概念：最大间隔。 最大间隔刻画着当前分类器与数据集的边界，以这两个分类器为例

# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
x_fit = np.linspace(0, 3)
# 画函数
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
# 画边距
plt.fill_between(x_fit, y_1 - 0.6, y_1 + 0.6, edgecolor='none', color='#AAAAAA', alpha=0.4)
y_2 = -0.3 * x_fit + 3
plt.plot(x_fit, y_2, '-k')
plt.fill_between(x_fit, y_2 - 0.4, y_2 + 0.4, edgecolor='none', color='#AAAAAA', alpha=0.4)

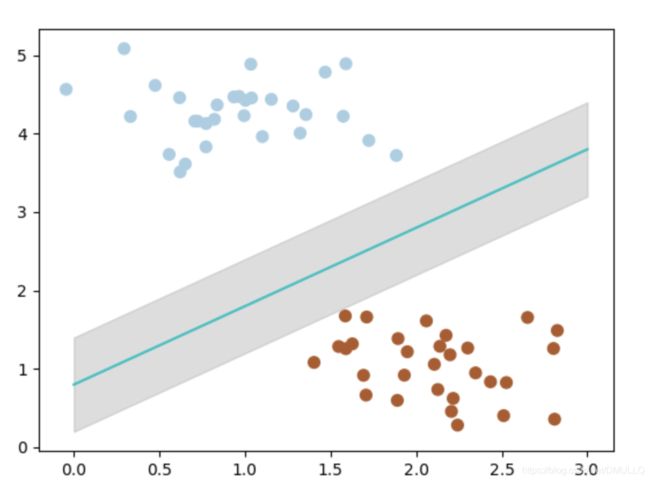
• 可以看到， 蓝色的线最大间隔是大于黑色的线的。 所以我们会选择蓝色的线作为我们的分类器。
• 那么，我们现在的分类器是最优分类器吗？ 或者说，有没有更好的分类器，它具有更大的间隔？ 答案是有的。 为了找出最优分类器，我们需要引入我们今天的主角：SVM

from sklearn.svm import SVC
# SVM 函数
clf = SVC(kernel='linear')
clf.fit(X, y)

# 最佳函数
w = clf.coef_[0]
a = -w[0] / w[1]
y_3 = a*x_fit - (clf.intercept_[0]) / w[1]
# 最大边距 下届
b_down = clf.support_vectors_[0]
y_down = a* x_fit + b_down[1] - a * b_down[0]
# 最大边距 上届
b_up = clf.support_vectors_[-1]
y_up = a* x_fit + b_up[1] - a * b_up[0]

# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 画函数
plt.plot(x_fit, y_3, '-c')
# 画边距
plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
# 画支持向量
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
 s=80, facecolors='none')

带黑边的点是距离当前分类器最近的点，我们称之为支持向量。
支持向量机为我们提供了在众多可能的分类器之间进行选择的原则，从而确保对未知数据集具有更高的泛化性。