1.7数算PPT选择汇总，PTA选择汇总，计算后缀表达式，中缀转后缀、前缀、快速排序

PTA选择汇总

在第一个位置后插入，注意是在后面插入，而不是前面；要移动49，为50-I，第25个的话，移25个

如果是插在前面，就移动50，N-I+1，注意是插在前面还是后面 

删第一个，要移49，即N-I，删第30个，移50-30=20 

就是除8取余 

数组大小为50，10+50-35 

F实指，R虚指，R+20-F=R+5=13 

F实指，那么为R+30-F%30=11 ,R虚指，即FR不都是实指，如果都是实指，就是R+M-F+1%M

如果有一个虚指，就是R+M-F%M 

归并趟数是LOGN

 

 后序与中序相反，后序为左右根，中序为左根右，那么都没有左孩子

根节点的中序前驱，前驱指的就是这个结点的左孩子的子树结点，然后最右边就一定没孩子了，不然的话不会访问到根节点

后序为左右根，中序为左根右，如果相同的话，就都没有右孩子 

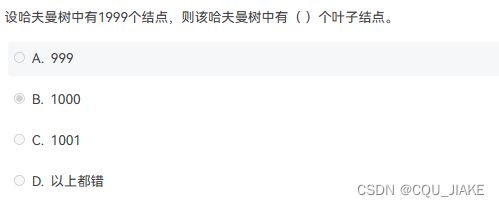
初始有N个叶子结点，那么构建出N-1个非叶子结点，总数量为2*N-1=1999，N=1000，即1000个叶子节点 

堆一定是完全二叉树，哈夫曼树不一定是完全二叉树，堆中可能存在度为1的结点

树转为二叉树，那么后序遍历和中序遍历相同；先序遍历和先序遍历相同

树不存在中序遍历

对于AVL树的高度，只有一个结点高1，2个高2，

FN=FN-1+FN-2+1，F3=4,F4=7,F5=12,F6=20.N代表的是高度，意思是要达到这个高度，所需要的最少的结点数

先右旋再左旋 

是有序的，不过顺序是从小到大

最后是2022，12，0，0，D

第一个查找失败的次数为3，2，1，1，2，然后即9/5=1.8 

G 可以是互相独立的点，

拓扑排序要求不能存在回路 

考虑，即回路上的边并不一定必须要去构造生成树 

 

最小生成树中任意两点间距并不一定是最短的，但总权和是最小的 

计算后缀表达式

class Solution {
public:
    int tod(string s){
        int sum=0;
        for(int i=0;i& tokens) {
        stackst;
        for(int i=0;i=c){
                    st.push(c-'0');
                }else{
                    int a=st.top();
                    st.pop();
                    int b=st.top();
                    st.pop();
                    switch(c){
                        case'+':st.push(a+b);break;
                        case'-':st.push(b-a);break;
                        case'*':st.push(a*b);break;
                        case'/':st.push(b/a);break;
                    }
                }
            }else{
                st.push(tod(tokens[i]));
            }
        }
        return st.top();
    }
};

中缀转前缀

中缀转后缀

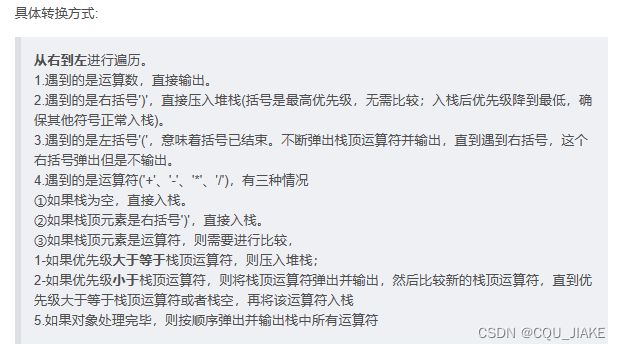
然后转后缀是要两个栈，一个输出栈，一个辅助栈，输出栈里的元素就是最后要输出的后缀表达式，

如果遇到数字，就直接加到输出栈里，如果遇到括号，就先放到辅助栈里

遇到运算符，首先判断辅助栈是不是空，是空的话就加到辅助栈里，表示做的第一个运算

就是一个是操作符栈，一个是数字栈，最后都给整到数字栈里去，遇到数字直接往数字栈里放，遇到操作符就往操作符栈里放，放的时候注意，第一要判断操作符栈是否为空，第二判断是否遇到了括号，其次判断优先级，

遇到优先级大的（指栈顶优先级比目前大），就栈顶元素先操作，把它加到操作数栈里去，遇到小的或同级的，就入操作符栈，最后再统一加入到数字栈里去

左括号只有遇到右括号才能消掉

这个用来得到优先级，

 

遍历中缀表达式，保证操作栈的栈顶是当前运算级最高的

class Solution {
public:
    struct Data {
        bool is_number {false};
        long long number {0};
        char op {'\0'};
        Data(bool set_is_number, long long set_number, char set_op) : is_number(set_is_number), number(set_number), op(set_op) {};
    };

    int calculate(string s) {
        // 去除所有空格
        std::string new_s1;
        for (char c : s) {
            if (c != ' ') {
                new_s1 += c;
            }
        }

        // (-n) -> (0-n)
        // (+n) -> (0+n) (本题没有，忽略)
        // 开头的-n -> 0-n
        // 开头的+n -> 0+n (本题没有，忽略)
        std::string new_s2;
        int n = new_s1.length();
        for (int i = 0; i < n; ++i) {
            if (new_s1[i] == '-' && (i == 0 || new_s1[i - 1] == '(')) {
                new_s2 += "0-";
            } else {
                new_s2 += new_s1[i];
            }
        }

        // 中缀表达式 -> 后缀表达式
        // 操作符优先级:：^（本题没有，忽略） > *、/（本题没有，忽略） > +、-
        // 左括号、右括号的优先级单独计算，因为无论定义左括号优先级最高，右括号优先级最低，还是左括号优先级最低，右括号优先级最高，在具体计算的不同逻辑中都无法统一处理
        // 相同优先级条件下，先出现的优先级更高(即，均是+、-，则先出现的比后出现的优先级级高，即相同优先级的运算符，先出现的先计算)
        // 转换过程：
        // 中缀表达式从前向后遍历过程中，保证op_stack的栈顶是当前操作符优先级最高的
        // 即，如果栈为空，或者当前操作符比栈顶操作符优先级高，则入栈
        // 遇到(，则认为优先级最高，无脑入栈
        // 遇到)，则认为优先级最低，不断弹栈到后缀表达式结果datas中，直到遇到(，操作符)不会入栈
        // 如果栈不为空，且当前操作符比栈顶操作符优先级低或相同(优先级相同时，先出现的优先级更高，需要先进行计算)，则不断弹栈到后缀表达式结果datas中，直到弹到栈为空，或当前操作符优先级比栈顶操作符元素的优先级高，或遇到(，弹栈后，将当前操作符压栈，即，该操作符入栈前，一定要保证所有优先级大于等于该操作符(实际等于时，先出现的优先级也要更高，要先计算)的操作符，都要先输出到后缀表达式结果datas中

        // 存储后缀表达式
        std::vector datas;
        // 存储操作符op的栈
        std::stack op_stack;

        // 中缀表达式 -> 后缀表达式
        // has_number是为了知道最后是否还有数字元素没有加入到datas中，因为每次遇到操作符才将cur_number写入，但是最后结尾有可能是数字，有可能是操作符)，而且数字可能为0，可能非0，无法判断，所以只能引入额外变量标记
        bool has_number = false;
        long long cur_number = 0;
        for (char c : new_s2) {
            if (c >= '0' && c <= '9') {
                // 数字
                has_number = true;
                cur_number = cur_number * 10 + c - '0';
            } else {
                // 操作符
                if (has_number) {
                    // 将上一个数字输出到后缀表达式结果datas中
                    datas.emplace_back(true, cur_number, '\0');
                    cur_number = 0;
                    has_number = false;
                }

                if (c == '(') {
                    // 遇到(，无脑入栈
                    op_stack.emplace(c);
                } else if (c == ')') {
                    // 遇到)，不断弹栈到后缀表达式结果datas中，直到遇到(，操作符)不会入栈
                    while (!op_stack.empty() && op_stack.top() != '(') {
                        char op = op_stack.top();
                        op_stack.pop();
                        datas.emplace_back(false, 0, op);
                    }

                    // 将'('弹栈
                    op_stack.pop();
                } else if (c == '+' || c == '-') {
                    if (op_stack.empty() || op_stack.top() == '(') {
                        // 如果栈为空，或者当前操作符比栈顶操作符优先级高，则入栈
                        op_stack.emplace(c);
                    } else {
                        // 如果栈不为空，且当前操作符比栈顶操作符优先级低或相同(优先级相同时，先出现的优先级更高，需要先进行计算)，则不断弹栈到后缀表达式结果datas中，直到弹到栈为空，或当前操作符优先级比栈顶操作符元素的优先级高，或遇到(，弹栈后，将当前操作符压栈，即，该操作符入栈前，一定要保证所有优先级大于等于该操作符(实际等于时，先出现的优先级也要更高，要先计算)的操作符，都要先输出到后缀表达式结果datas中
                        while (!op_stack.empty() && (op_stack.top() == '+' || op_stack.top() == '-')) {
                            // 这里如果遇到(就不要再弹了，说明这些都是在一组()内处理的部分
                            char op = op_stack.top();
                            op_stack.pop();
                            datas.emplace_back(false, 0, op);
                        }

                        // 将当前操作符压栈
                        op_stack.emplace(c);
                    }
                }
            }
        }
        if (has_number) {
            // 如果原中缀表达式最后一个字符不是)，则最后一个数字还没有输出到后缀表达式结果datas中
            datas.emplace_back(true, cur_number, '\0');
        }
        while (!op_stack.empty()) {
            // 将栈中剩余操作符依次弹栈到后缀表达式结果datas中
            char op = op_stack.top();
            op_stack.pop();
            datas.emplace_back(false, 0, op);
        }

        // 计算后缀表达式
        // 此时后缀表达式结果datas中，只包括数字、+、-，不会再存在括号

        // 存储操作数num的栈
        std::stack num_stack;

        for (const Data& data : datas) {
            if (data.is_number) {
                // 如果是数字，就压栈
                num_stack.emplace(data.number);
            } else {
                // 如果是操作符，就进行相应计算
                // 先弹栈的是右操作数，后弹栈的是左操作数
                long long a = num_stack.top();
                num_stack.pop();
                long long b = num_stack.top();
                num_stack.pop();
                if (data.op == '+') {
                    num_stack.emplace(b + a);
                } else if (data.op == '-') {
                    num_stack.emplace(b - a);
                }
            }
        }

        return num_stack.top();
    }
};

快速排序

、定义一个begin和一个end，begin从左向右走，end从右向左走。（需要注意的是：若选择最左边的数据作为key，则需要end先走；若选择最右边的数据作为key，则需要bengin先走）

就是说如果基值是左边第一个，最后就要用右指针；是右边第一个，就用左指针为最后的

//快速排序   hoare版本(左右指针法)
void QuickSort(int* arr, int begin, int end)
{
	//只有一个数或区间不存在
	if (begin >= end)
		return;
	int left = begin;
	int right = end;
	//选左边为key
	int keyi = begin;
	while (begin < end)
	{
		//右边选小   等号防止和key值相等    防止顺序begin和end越界
		while (arr[end] >= arr[keyi] && begin < end)
		{
			--end;
		}
		//左边选大
		while (arr[begin] <= arr[keyi] && begin < end)
		{
			++begin;
		}
		//小的换到右边，大的换到左边
		swap(&arr[begin], &arr[end]);
	}
	swap(&arr[keyi], &arr[end]);
	keyi = end;
	//[left,keyi-1]keyi[keyi+1,right]
	QuickSort(arr, left, keyi - 1);
	QuickSort(arr,keyi + 1,right);
}

#include
using namespace std;
const int maxn = 1e5 + 5;
int n, arr[maxn];
void swap(int i, int j) {
    int temp = arr[j];
    arr[j] = arr[i];
    arr[i] = temp;
}
void quick(int begin, int end) {
    if (begin >= end)return;
    int i = begin, j = end, key = arr[begin];
    while (i!=j) {
        while (i != j && arr[j] >= key) {
            j--;
        }
        while (i != j && arr[i] <= key) {
            i++;//必须得带上等号，不然的话，如果有重复元素在这里，那么左右都不会动，就形成了死循环
        }
        if(i!=j)swap(i, j);
    }
    swap(begin, j);
    quick(begin, j - 1);
    quick(j + 1, end);
}
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> arr[i];
    }
    quick(1, n);
    for (int i = 1; i <= n; i++) {
        cout << arr[i] << " ";
    }
    return 0;
}

就是注意，快排一定一定一定一定要带上=号，不带等于快排一定会出错 

PPT 

 

C生成树有N-1条边，再加上任意一条边后就一定会产生回路 

C在回路上删去任意一条边都会使其再变回生成树 

P可以接受图中有负边 

只有可以缩短距离才会入队，然后dis数组始终保存的是当下距离最短的路径长度

ACD对 。对于B,如果第一次入队的时候就是最小的距离，那么后续的所有入度都不会再入队

ABD 

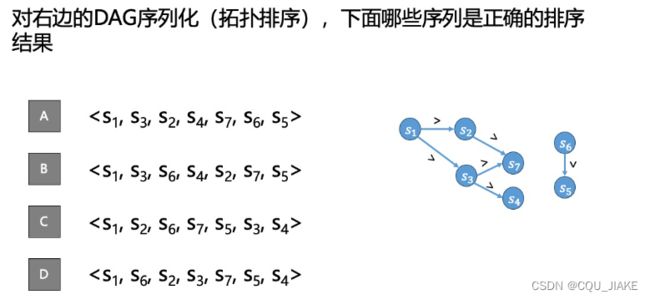
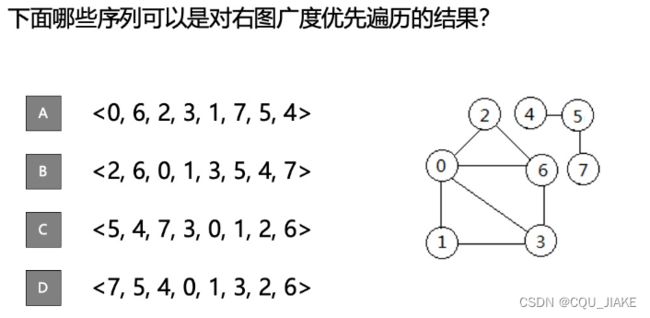
首先要访问根节点才能去访问子节点，所以是先序遍历，以及层序遍历AD 

C也可以

因为后序颠倒的话，是根右左，同样满足是先访问父节点，再访问子节点的，所以可以满足是拓扑排序

AD 

对于B，对于结点1，在下一层时不是第一个被访问到的，因为6不连接1，下一层的第一个应该是3，然后才是1

ABD

对于能够一笔画的图，应该满足：
1.图连通，有且只有两个奇点（度为奇数的点），则存在欧拉路（不一定回到原点）。
2.图连通，且没有奇点，则存在欧拉回路（回原点）。 

ACBD点都是度为 奇数的结点，添一条边可以使两个结点的度增加1，所以加一条边后可以形成欧拉路，再加一条变可以构成欧拉回路

C，如果要是邻居，那么必定可以到达

D，边数最大的话，是每个结点都和其它N-1个结点有一条边，那么共有N(N-1)，这里是有向图，所以不用除以2，如果是无向图的话，就要除以2；然后最小的话，由于是强连通图，所以最少就是一个环，共N条边；N-1条边可以构成一个树，树再加任意一边可构成回路

AD，对于E，删除一个结点，要遍历这个结点所有的边，所以不是O1

ABC ，对于B的，添加的话是O1复杂度，删除的话是ON，计算出度是ON,计算入度的话，就需要遍历所有的结点，是一个OEV的复杂度

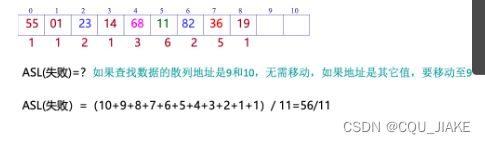
对于查找成功的 ，就是从指数位置到存储位置的区间里的元素个数（不是步长），

对于查找失败的，是从指数位置到空端点的元素个数，包含空端点

 平均查找成功，就是计算出哈希值后到存储位置的元素个数，要除以存储元素个数

平均失败，是是每个哈希值到失败，第一个空端点的元素个数，要除以所有可能哈希值的总数

#include
using namespace std;
int n, m, p, arr[10000], num, ts = 0, tf = 0;
int main() {
    cin >> n >> m >> p;
    for (int i = 1; i <= n; i++) {
        cin >> num;
        int index = num % p, cnt = 1;
        while (arr[index]&&arr[index]!=num) {
            index = (index + 1) % m;
            cnt++;
        }
        arr[index] = num;
        ts += cnt;
    }
    cout << ts << "/" << n;
    for (int i = 0; i < p; i++) {
        int cnt = 1, index = i;
        while (arr[index]) {
            index = (index + 1) % m;
            cnt++;
        }
        tf += cnt;
    }
    cout << tf << "/" << p;
    return 0;
}

ABC 

自己的序列本身就是中序序列，ACD 

前序为根左右，依据中序为1~9重构BST树来进行判断 

D 

ABCD 

i/2是最后一个非叶子结点，即1015，最小值的话，必定不是非叶子结点，因为没有比他小的了，所以就是最后一个非叶子结点+1后的都可能，取1016 

B 

C 

堆可以有度为1的结点，哈夫曼树不会有；

堆与哈夫曼树都是完全二叉树 

ADCB

入度=出度，N-1=2N2+N1=N2+N1+N0-1，有N0=N2+1，所有 结点数为N=2*N2+N1+1，由于为完全二叉树，度为1要么为1要么没有，这里是奇数，所以一定没有，为0

A 

 

B 

前序是根左右，中序是左根右，相同的话就都没有左孩子C 

B，N=2*N2+N1-1,如果含偶数个结点N为偶数，2*N2-1是奇数，所以N1一定是奇数，即B 

D，A不对 

最小的话，就是一个序列都比另一个序列的最小元素小，比较N次

最大的话就是交叉，开始小，后面大，一共2n个，所以2n-1，最后一个就是最大的，不用比较

A 

bc 

C 

B 

就是说一个希尔排序，gap是一半 

D例如，序列是1,2,1,3,1,4,1,5,1,6,1,7,…

D 

C 

 

 

4，F在6，R在3，MAX=10。13-6

D 6+10-3+1

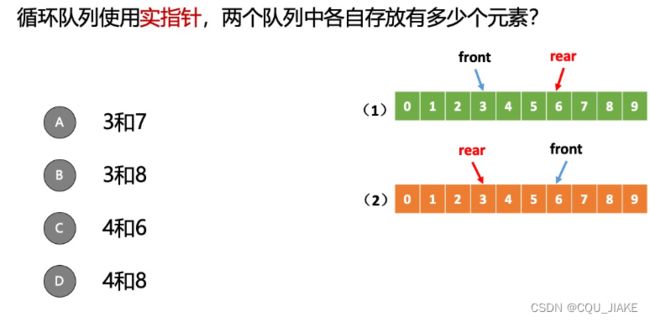
如果用的是虚指针，那么队列中元素数量是(R-F+M) %M,即不包含区间两个端点，而是只有一个端点，这个包含的端点，就是尾指针所实指的那个元素端点，而不包含头指针】

如果用的是实指针，计算就要用（R-F+1+M)%M，这样R-F+1计算就是算出来的是含两个区间端点的元素个数

（6-3+10）%10=3，（3+10-6）%10=7，A

C